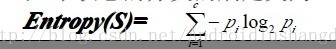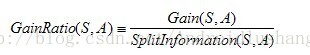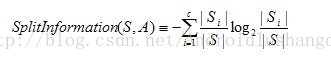<机器学习实战>读书笔记--决策树
1、决策树的构造
createBranch伪代码:
检测数据集中的每个子项是否属于同一分类:
IF SO RETURN 类标签
ELSE
寻找划分数据集的最好特征
划分数据集
创建分支节点
FOR 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
RETURN 分支节点
划分数据集的大原则:将无序的数据变的更加有序。在划分数据集之前之后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择
熵定义为信息的期望值。熵越大越离散。
计算给定数据集的香农熵
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
2.决策树的构造算法
ID3算法
ID3算法是一种分类决策树算法。他通过一系列的规则,将数据最后分类成决策树的形式。分类的根据是用到了熵这个概念。熵在物理这门学科中就已经出现过,表示是一个物质的稳定度,在这里就是分类的纯度的一个概念。公式为:
C4.5算法
C4.5与ID3在核心的算法是一样的,但是有一点所采用的办法是不同的,C4.5采用了信息增益率作为划分的根据,克服了ID3算法中采用信息增益划分导致属性选择偏向取值多的属性。信息增益率的公式为:
分母的位置是分裂因子,他的计算公式为:
CART算法
CART算法对于属性的值采用的是基于Gini系数值的方式做比较,gini某个属性的某次值的划分的gini指数的值为:

<机器学习实战>读书笔记--决策树的更多相关文章
- 机器学习实战 - 读书笔记(13) - 利用PCA来简化数据
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第13章 - 利用PCA来简化数据. 这里介绍,机器学习中的降维技术,可简化样品数据. ...
- 机器学习实战 - 读书笔记(12) - 使用FP-growth算法来高效发现频繁项集
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第12章 - 使用FP-growth算法来高效发现频繁项集. 基本概念 FP-growt ...
- 机器学习实战 - 读书笔记(11) - 使用Apriori算法进行关联分析
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第11章 - 使用Apriori算法进行关联分析. 基本概念 关联分析(associat ...
- 机器学习实战 - 读书笔记(07) - 利用AdaBoost元算法提高分类性能
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习笔记,这次是第7章 - 利用AdaBoost元算法提高分类性能. 核心思想 在使用某个特定的算法是, ...
- 机器学习实战 - 读书笔记(06) – SVM支持向量机
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习笔记,这次是第6章:SVM 支持向量机. 支持向量机不是很好被理解,主要是因为里面涉及到了许多数学知 ...
- 【转载】 机器学习实战 - 读书笔记(07) - 利用AdaBoost元算法提高分类性能
原文地址: https://www.cnblogs.com/steven-yang/p/5686473.html ------------------------------------------- ...
- 机器学习实战 - 读书笔记(14) - 利用SVD简化数据
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习心得,这次是第14章 - 利用SVD简化数据. 这里介绍,机器学习中的降维技术,可简化样品数据. 基 ...
- 机器学习实战读书笔记(二)k-近邻算法
knn算法: 1.优点:精度高.对异常值不敏感.无数据输入假定 2.缺点:计算复杂度高.空间复杂度高. 3.适用数据范围:数值型和标称型. 一般流程: 1.收集数据 2.准备数据 3.分析数据 4.训 ...
- <机器学习实战>读书笔记--朴素贝叶斯
1.朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法, 最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model, ...
随机推荐
- visual studio code中使用emmet插件在.vue文件失效
使用visual studio code编辑.vue文件时,emmet插件无法使用,可以通过以下两种试解决: 1.文件→设置,在右侧窗口添加以下代码: "emmet.syntaxProfil ...
- oracle 批量删除触发器
--生成删除触发器的语句 select 'drop trigger "'||trigger_name||'";' from all_triggers where TRIGGER_ ...
- Pi 实现VLC网络视频监控
安装摄像头 将Pi的原装摄像头安装在pi上面 ssh连接pi 通过xshell或者putty等工具连接ssh 安装VLC $ sudo apt-get update $ sudo apt-get in ...
- WORD wFormatTag; /* format type */ //设置波形声音的格式
0x0000 Microsoft Unknown Wave Format 0x0001 Microsoft PCM Format 0x0002 ...
- 第八届蓝桥杯JavaB---承压计算
标题:承压计算 X星球的高科技实验室中整齐地堆放着某批珍贵金属原料. 每块金属原料的外形.尺寸完全一致,但重量不同. 金属材料被严格地堆放成金字塔形. 7 5 8 7 8 8 9 2 7 2 8 1 ...
- C++中运算符的优先级
运算符挺多的,很难一一记住他们的优先级,在此去别人博客复制以下内容,供自己以后学习. 优先级 运算符 含 义 要求运算 对象的个数 结合方向 1 () [] -> . 圆括号 下标运算符 ...
- Elastic Search 5.x Nest Multiple Queries C#
I'm using C# with those nuget packeges; <package id="Elasticsearch.Net" version="5 ...
- jdk命令行工具(一)
1.概述 熟悉java开发的人应该都知道在jdk的bin目录下有许多的工具,这些工具主要用于监视虚拟机和故障处理.这些故障处理工具被Sun公司称作为“礼物”附赠给JDK的使用者,并在软件的使用说明中把 ...
- Java_多线程2_线程池
线程池(pool): 线程池的作用: 1.节省资源,减少线程的数量和创建销毁线程的开销2.合理的管理线程的分配 线程池的创建: 1.newCachedThreadPool //优点:很灵活,弹性的线程 ...
- c++之随堂笔记
1.指针篇 给指针赋值时,只能等号右边只能使用&符号将一个对象的地址赋值给指针,不能直接把一个具体的数或者字符串直接赋值给指针. 举例: int* ptr_num = 100; //这种写法 ...