L3-009 长城（30 分）

正如我们所知，中国古代长城的建造是为了抵御外敌入侵。在长城上，建造了许多烽火台。每个烽火台都监视着一个特定的地区范围。一旦某个地区有外敌入侵，值守在对应烽火台上的士兵就会将敌情通报给周围的烽火台，并迅速接力地传递到总部。

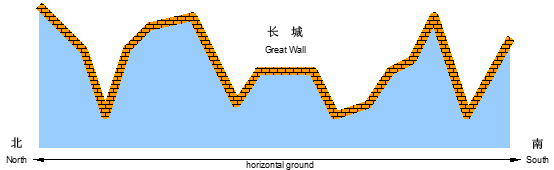
现在如图1所示，若水平为南北方向、垂直为海拔高度方向，假设长城就是依次相联的一系列线段，而且在此范围内的任一垂直线与这些线段有且仅有唯一的交点。

图 1

进一步地，假设烽火台只能建造在线段的端点处。我们认为烽火台本身是没有高度的，每个烽火台只负责向北方（图1中向左）瞭望，而且一旦有外敌入侵，只要敌人与烽火台之间未被山体遮挡，哨兵就会立即察觉。当然，按照这一军规，对于南侧的敌情各烽火台并不负责任。一旦哨兵发现敌情，他就会立即以狼烟或烽火的形式，向其南方的烽火台传递警报，直到位于最南侧的总部。

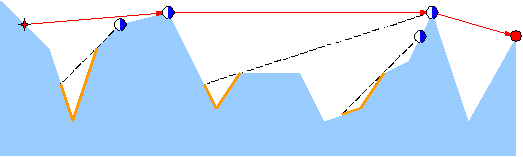
以图2中的长城为例，负责守卫的四个烽火台用蓝白圆点示意，最南侧的总部用红色圆点示意。如果红色星形标示的地方出现敌情，将被哨兵们发现并沿红色折线将警报传递到总部。当然，就这个例子而言只需两个烽火台的协作，但其他位置的敌情可能需要更多。

然而反过来，即便这里的4个烽火台全部参与，依然有不能覆盖的（黄色）区域。

图 2

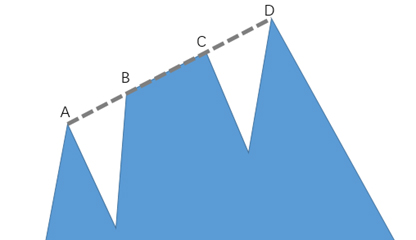
另外，为避免歧义，我们在这里约定，与某个烽火台的视线刚好相切的区域都认为可以被该烽火台所监视。以图3中的长城为例，若A、B、C、D点均共线，且在D点设置一处烽火台，则A、B、C以及线段BC上的任何一点都在该烽火台的监视范围之内。

图 3

好了，倘若你是秦始皇的太尉，为不致出现更多孟姜女式的悲剧，如何在保证长城安全的前提下，使消耗的民力（建造的烽火台）最少呢？

输入格式：

输入在第一行给出一个正整数N（3 ≤ N ≤），即刻画长城边缘的折线顶点（含起点和终点）数。随后N行，每行给出一个顶点的x和y坐标，其间以空格分隔。注意顶点从南到北依次给出，第一个顶点为总部所在位置。坐标为区间[内的整数，且没有重合点。

输出格式：

在一行中输出所需建造烽火台（不含总部）的最少数目。

输入样例：

输出样例：

2
题目给出测试样例，可以用excel画出折线图：

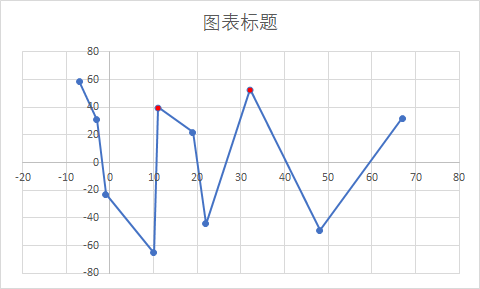
显然最右边的点是总部，两个红点是烽火台的位置，这两个点都是向上突起的点，挡住视线，所以要设烽火台，那么怎么找到这样的点。

用栈来辅助判断，依次把点加入栈，当要加入一个新的点时，判断栈顶的点是否会成为凸点，如果不会就出栈，直到遇到会的，那么就是可以设置烽火台的点了，这个时候要记录这个点，并把新点加入栈。

代码：

#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
int n,c;
long long x[],y[];
int s[];
set<int> ans;
bool check(int a,int b,int c) {//按照斜率来看b是凹点时，返回true,或者是通过向量ac和ab的叉乘积小于0（ab在ac下面）等于0（三点共线）返回true
    return (y[b] - y[a]) * (x[c] - x[a]) <= (y[c] - y[a]) * (x[b] - x[a]);
}
int main() {
    scanf("%d",&n);
    for(int i = ;i < n;i ++) {
        scanf("%lld%lld",&x[i],&y[i]);
        if(c >= ) {
            while(c >=  && check(i,s[c - ],s[c - ])) c --;
            if(s[c - ]) ans.insert(s[c - ]);//总部不算
        }
        s[c ++] = i;
    }
    printf("%d",ans.size());
}