P4005 小 Y 和地铁

题目描述

小 Y 是一个爱好旅行的 OIer。一天，她来到了一个新的城市。由于不熟悉那里的交通系统，她选择了坐地铁。

她发现每条地铁线路可以看成平面上的一条曲线，不同线路的交点处一定会设有

换乘站。通过调查得知，没有线路是环线，也没有线路与自身相交。任意两条不同的线路只会在若干个点上相交，没有重合的部分，且没有三线共点的情况。即，如图所示的情况都是不存在的：

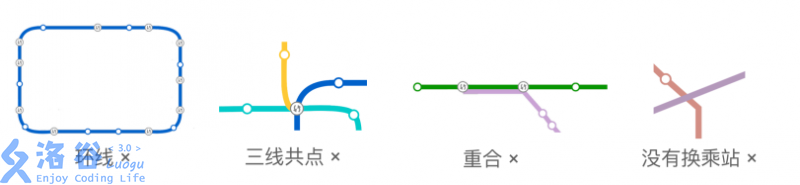
小 Y 坐着地铁 0 号线，路上依次经过了 n 个换乘站。她记下了每个换乘站可以换乘的线路编号，发现每条线路与她所乘坐的线路最多只有 2 个换乘站。现在小 Y 想知道，除掉她经过的换乘站以外，这个城市里最少有几个换乘站。只有你告诉她正确的答案，她才会答应下次带你去玩呢。

输入输出格式

输入格式：

从文件 metro.in 中读入数据。

请.注.意.本.题.有.多.组.输.入.数.据。

输入数据的第一行是一个整数 T，表示输入数据的组数。接下来依次给出每组数据。

对于每组数据，第一行是一个整数 n，表示小 Y 经过的换乘站的数目。第二行为 n个用空格隔开的整数，依次表示每个换乘站的可以换乘的线路编号。这些编号都在 1 ~n 之内。

输出格式：

输出到文件 metro.out 中。

对于每组输入数据，输出一行一个整数，表示除掉这 n 个换乘站之外，最少有几个换乘站。

输入输出样例

输入样例#1：

4 
4

1 2 1 2

8

1 2 3 4 1 2 3 4

5

5 4 3 3 5

8

1 2 3 4 1 3 2 4

输出样例#1：

说明

【样例 1 解释】

对于样例的前两组数据，一种可能的最优答案如下图所示。

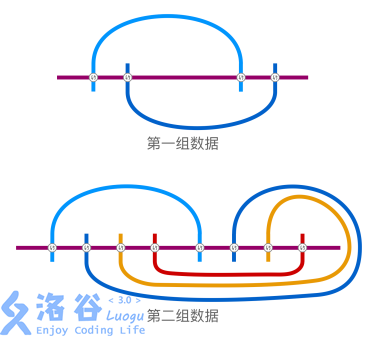
【子任务】

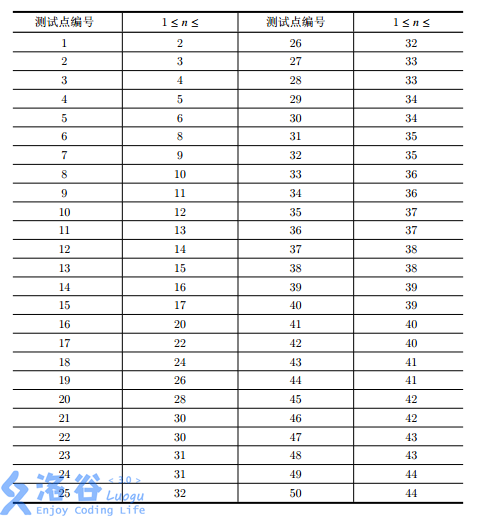
一共有 50 个测试点，每个测试点 2 分。你只有在答案完全正确时才能得到该测试点的全部分数，否则不得分。

对于所有测试点，以及对于样例， 1 ≤ T ≤ 100; 1 ≤ n ≤ 44。对于每个测试点， n 的范围如下表：

Solution：

　　本题ZYYS，绝世搜索好题。

　　题意有些晦涩，总结后不难发现实际路线只有$4$种情况：

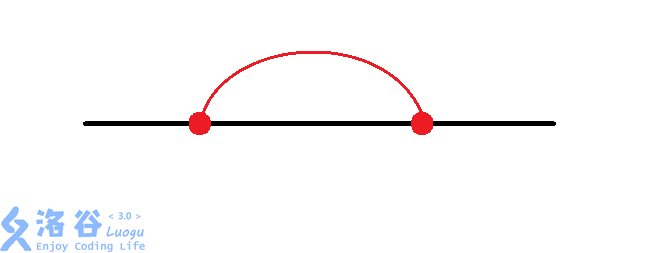
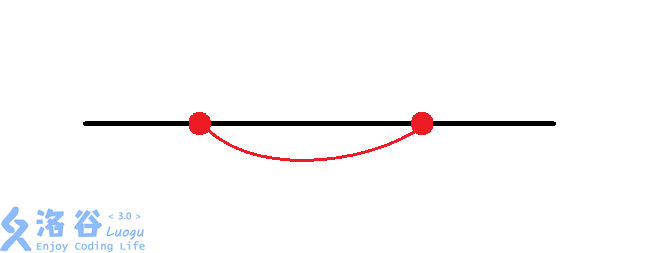
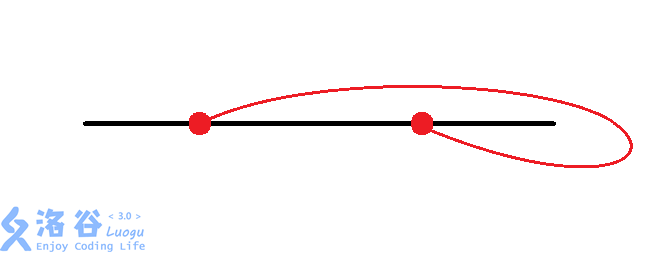
　　至于洛谷题解中的开始8种情况的另外4种，贪心的想到，完全没有必要那样建，比如：

　　和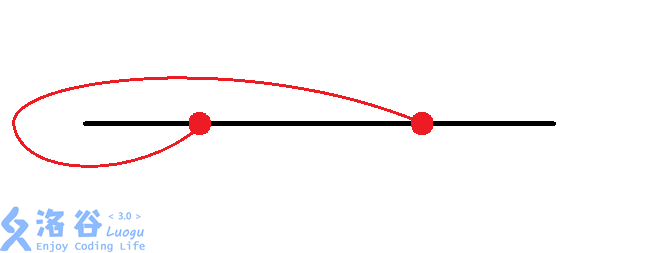

　　由于要使各曲线的交点尽量少，那么上面两幅图肯定是没有这幅图优秀的：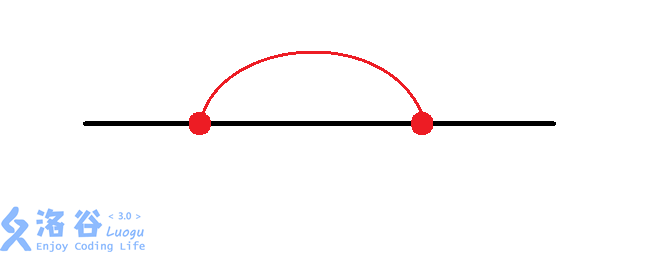

　　然后在最上面说的4种情形中，由于上部的曲线不可能和下部的曲线相交，所以可以将其上下分开看，而既有上部又有下部的图直接将其当作两个部分的曲线合并，比如：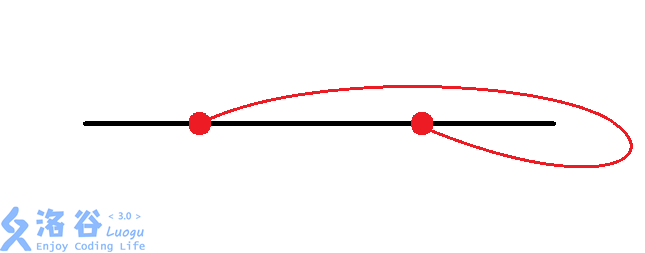

理解为上部的曲线$[l,n]$+下部的曲线$[r,n]$就好了。

　　然后对于同上或同下的两个曲线$[l1,r1],[l2,r2]$，显然只有$l2\leq r1\leq r2$时才会有交点，那么计算一段曲线会产生多少交点，就得统计区间$[l,r]$之间的已有$r$个数，单点修改区间查询直接想到树状数组。

　　这样就能直接暴力搜索，枚举每条曲线的形态，对于既有上部和下部的曲线，发现可以和另一条单部曲线合并成环，比如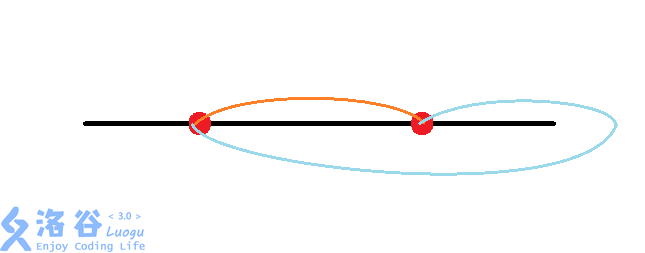：从左到右枚举曲线状态，当前状态只受左边的影响，由于$l$左边的曲线状态已确定，而$r$是确定的，所以当前$[l,r]$的最优情况直接贪心选择两种方式的与左边交点的最小个数就好了，另一种情况同理就好了。

　　时间复杂度$O(2^{\frac{n}{2}}\log n)$。

代码：

/*Code by 520 -- 9.2*/

#include<bits/stdc++.h>

#define il inline

#define ll long long

#define RE register

#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)

#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)

using namespace std;

const int N=;

int n,a[N],T,l[N],r[N],ans,num;

struct node{

    int c[N];

    void clear(){memset(c,,sizeof(c));}

    void add(int x,int k){while(x<=n)c[x]+=k,x+=x&-x;}

    int sum(int x){int ans=;while(x)ans+=c[x],x-=x&-x;return ans;}

    int query(int l,int r){return sum(r)-sum(l-);}

}up,down;

int gi(){

    int a=;char x=getchar();

    while(x<''||x>'')x=getchar();

    while(x>=''&&x<='')a=(a<<)+(a<<)+(x^),x=getchar();

    return a;

}

void dfs(int x,int tot){

    if(x>num){ans=min(ans,tot);return;}

    if(tot>=ans)return;

    int upp=min(up.query(l[x],r[x]),down.query(l[x],n)+up.query(r[x],n));

    up.add(r[x],),dfs(x+,tot+upp),up.add(r[x],-);

    int downn=min(down.query(l[x],r[x]),up.query(l[x],n)+down.query(r[x],n));

    down.add(r[x],),dfs(x+,tot+downn),down.add(r[x],-);

}

il void solve(){

    for(T=gi();T;--T){

        scanf("%d",&n),ans=0x7fffffff,num=;

        For(i,,n) a[i]=gi();

        For(i,,n) For(j,i+,n) if(a[i]==a[j]){l[++num]=i,r[num]=j;break;}

        up.clear(),down.clear();

        dfs(,);

        printf("%d\n",ans);

    }

}

int main(){

    solve();

    return ;

}