poj3608 Bridge Across Islands

地址：http://poj.org/problem?id=3608

题目：

Bridge Across Islands

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11259		Accepted: 3307		Special Judge

Description

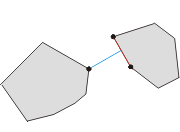
Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.

Input

The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].

Output

For each test case output the minimal distance. An error within 0.001 is acceptable.

Sample Input

4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0

Sample Output

1.00000

Source

POJ Founder Monthly Contest – 2008.06.29, Lei Tao

思路：

　　两凸包间的最近点对，套模板。

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <algorithm>

 using namespace std;
 const double PI = acos(-1.0);
 const double eps = 1e-;

 /****************常用函数***************/
 //判断ta与tb的大小关系
 int sgn( double ta, double tb)
 {
     if(fabs(ta-tb)<eps)return ;
     if(ta<tb)   return -;
     return ;
 }

 //点
 class Point
 {
 public:

     double x, y;

     Point(){}
     Point( double tx, double ty){ x = tx, y = ty;}

     bool operator < (const Point &_se) const
     {
         return x<_se.x || (x==_se.x && y<_se.y);
     }
     friend Point operator + (const Point &_st,const Point &_se)
     {
         return Point(_st.x + _se.x, _st.y + _se.y);
     }
     friend Point operator - (const Point &_st,const Point &_se)
     {
         return Point(_st.x - _se.x, _st.y - _se.y);
     }
     //点位置相同(double类型)
     bool operator == (const Point &_off)const
     {
         return  sgn(x, _off.x) ==  && sgn(y, _off.y) == ;
     }

 };

 /****************常用函数***************/
 //点乘
 double dot(const Point &po,const Point &ps,const Point &pe)
 {
     return (ps.x - po.x) * (pe.x - po.x) + (ps.y - po.y) * (pe.y - po.y);
 }
 //叉乘
 double xmult(const Point &po,const Point &ps,const Point &pe)
 {
     return (ps.x - po.x) * (pe.y - po.y) - (pe.x - po.x) * (ps.y - po.y);
 }
 //两点间距离的平方
 double getdis2(const Point &st,const Point &se)
 {
     return (st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y);
 }
 //两点间距离
 double getdis(const Point &st,const Point &se)
 {
     return sqrt((st.x - se.x) * (st.x - se.x) + (st.y - se.y) * (st.y - se.y));
 }

 //两点表示的向量
 class Line
 {
 public:

     Point s, e;//两点表示，起点[s]，终点[e]
     double a, b, c;//一般式,ax+by+c=0
     double angle;//向量的角度，[-pi,pi]

     Line(){}
     Line( Point ts, Point te):s(ts),e(te){}//get_angle();}
     Line(double _a,double _b,double _c):a(_a),b(_b),c(_c){}

     //排序用
     bool operator < (const Line &ta)const
     {
         return angle<ta.angle;
     }
     //向量与向量的叉乘
     friend double operator / ( const Line &_st, const  Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.y - _se.s.y) - (_st.e.y - _st.s.y) * (_se.e.x - _se.s.x);
     }
     //向量间的点乘
     friend double operator *( const Line &_st, const  Line &_se)
     {
         return (_st.e.x - _st.s.x) * (_se.e.x - _se.s.x) - (_st.e.y - _st.s.y) * (_se.e.y - _se.s.y);
     }
     //从两点表示转换为一般表示
     //a=y2-y1,b=x1-x2,c=x2*y1-x1*y2
     bool pton()
     {
         a = e.y - s.y;
         b = s.x - e.x;
         c = e.x * s.y - e.y * s.x;
         return true;
     }
     //半平面交用
     //点在向量左边（右边的小于号改成大于号即可,在对应直线上则加上=号）
     friend bool operator < (const Point &_Off, const Line &_Ori)
     {
         return (_Ori.e.y - _Ori.s.y) * (_Off.x - _Ori.s.x)
             < (_Off.y - _Ori.s.y) * (_Ori.e.x - _Ori.s.x);
     }
     //求直线或向量的角度
     double get_angle( bool isVector = true)
     {
         angle = atan2( e.y - s.y, e.x - s.x);
         if(!isVector && angle < )
             angle += PI;
         return angle;
     }

     //点在线段或直线上 1:点在直线上 2点在s,e所在矩形内
     bool has(const Point &_Off, bool isSegment = false) const
     {
         bool ff = sgn( xmult( s, e, _Off), ) == ;
         if( !isSegment) return ff;
         return ff
             && sgn(_Off.x - min(s.x, e.x), ) >=  && sgn(_Off.x - max(s.x, e.x), ) <=
             && sgn(_Off.y - min(s.y, e.y), ) >=  && sgn(_Off.y - max(s.y, e.y), ) <= ;
     }

     //点到直线/线段的距离
     double dis(const Point &_Off, bool isSegment = false)
     {
         ///化为一般式
         pton();
         //到直线垂足的距离
         double td = (a * _Off.x + b * _Off.y + c) / sqrt(a * a + b * b);
         //如果是线段判断垂足
         if(isSegment)
         {
             double xp = (b * b * _Off.x - a * b * _Off.y - a * c) / ( a * a + b * b);
             double yp = (-a * b * _Off.x + a * a * _Off.y - b * c) / (a * a + b * b);
             double xb = max(s.x, e.x);
             double yb = max(s.y, e.y);
             double xs = s.x + e.x - xb;
             double ys = s.y + e.y - yb;
            if(xp > xb + eps || xp < xs - eps || yp > yb + eps || yp < ys - eps)
                 td = min( getdis(_Off,s), getdis(_Off,e));
         }
         return fabs(td);
     }

     //关于直线对称的点
     Point mirror(const Point &_Off)
     {
         ///注意先转为一般式
         Point ret;
         double d = a * a + b * b;
         ret.x = (b * b * _Off.x - a * a * _Off.x -  * a * b * _Off.y -  * a * c) / d;
         ret.y = (a * a * _Off.y - b * b * _Off.y -  * a * b * _Off.x -  * b * c) / d;
         return ret;
     }
     //计算两点的中垂线
     static Line ppline(const Point &_a,const Point &_b)
     {
         Line ret;
         ret.s.x = (_a.x + _b.x) / ;
         ret.s.y = (_a.y + _b.y) / ;
         //一般式
         ret.a = _b.x - _a.x;
         ret.b = _b.y - _a.y;
         ret.c = (_a.y - _b.y) * ret.s.y + (_a.x - _b.x) * ret.s.x;
         //两点式
         if(fabs(ret.a) > eps)
         {
             ret.e.y = 0.0;
             ret.e.x = - ret.c / ret.a;
             if(ret.e == ret. s)
             {
                 ret.e.y = 1e10;
                 ret.e.x = - (ret.c - ret.b * ret.e.y) / ret.a;
             }
         }
         else
         {
             ret.e.x = 0.0;
             ret.e.y = - ret.c / ret.b;
             if(ret.e == ret. s)
             {
                 ret.e.x = 1e10;
                 ret.e.y = - (ret.c - ret.a * ret.e.x) / ret.b;
             }
         }
         return ret;
     }

     //------------直线和直线（向量）-------------
     //向量向左边平移t的距离
     Line& moveLine( double t)
     {
         Point of;
         of = Point( -( e.y - s.y), e.x - s.x);
         double dis = sqrt( of.x * of.x + of.y * of.y);
         of.x= of.x * t / dis, of.y = of.y * t / dis;
         s = s + of, e = e + of;
         return *this;
     }
     //直线重合
     static bool equal(const Line &_st,const Line &_se)
     {
         return _st.has( _se.e) && _se.has( _st.s);
     }
     //直线平行
     static bool parallel(const Line &_st,const Line &_se)
     {
         return sgn( _st / _se, ) == ;
     }
     //两直线（线段）交点
     //返回-1代表平行，0代表重合，1代表相交
     static bool crossLPt(const Line &_st,const Line &_se, Point &ret)
     {
         if(parallel(_st,_se))
         {
             if(Line::equal(_st,_se)) return ;
             return -;
         }
         ret = _st.s;
         double t = ( Line(_st.s,_se.s) / _se) / ( _st / _se);
         ret.x += (_st.e.x - _st.s.x) * t;
         ret.y += (_st.e.y - _st.s.y) * t;
         return ;
     }
     //------------线段和直线（向量）----------
     //直线和线段相交
     //参数：直线[_st],线段[_se]
     friend bool crossSL( Line &_st, Line &_se)
     {
         return sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.e), ) >= ;
     }

     //判断线段是否相交(注意添加eps)
     static bool isCrossSS( const Line &_st, const  Line &_se)
     {
         //1.快速排斥试验判断以两条线段为对角线的两个矩形是否相交
         //2.跨立试验（等于0时端点重合）
         return
             max(_st.s.x, _st.e.x) >= min(_se.s.x, _se.e.x) &&
             max(_se.s.x, _se.e.x) >= min(_st.s.x, _st.e.x) &&
             max(_st.s.y, _st.e.y) >= min(_se.s.y, _se.e.y) &&
             max(_se.s.y, _se.e.y) >= min(_st.s.y, _st.e.y) &&
             sgn( xmult( _se.s, _st.s, _se.e) * xmult( _se.s, _se.e, _st.s), ) >=  &&
             sgn( xmult( _st.s, _se.s, _st.e) * xmult( _st.s, _st.e, _se.s), ) >= ;
     }
 };

 //寻找凸包的graham 扫描法所需的排序函数
 Point gsort;
 bool gcmp( const Point &ta, const Point &tb)/// 选取与最后一条确定边夹角最小的点，即余弦值最大者
 {
     double tmp = xmult( gsort, ta, tb);
     if( fabs( tmp) < eps)
         return getdis( gsort, ta) < getdis( gsort, tb);
     else if( tmp > )
         return ;
     return ;
 }

 class Polygon
 {
 public:
     const static int maxpn = 5e4+;
     Point pt[maxpn];//点（顺时针或逆时针）
     Line dq[maxpn]; //求半平面交打开注释
     int n;//点的个数

     //求多边形面积，多边形内点必须顺时针或逆时针
     double area()
     {
         double ans = 0.0;
         for(int i = ; i < n; i ++)
         {
             int nt = (i + ) % n;
             ans += pt[i].x * pt[nt].y - pt[nt].x * pt[i].y;
         }
         return fabs( ans / 2.0);
     }
     //求多边形重心，多边形内点必须顺时针或逆时针
     Point gravity()
     {
         Point ans;
         ans.x = ans.y = 0.0;
         double area = 0.0;
         for(int i = ; i < n; i ++)
         {
             int nt = (i + ) % n;
             double tp = pt[i].x * pt[nt].y - pt[nt].x * pt[i].y;
             area += tp;
             ans.x += tp * (pt[i].x + pt[nt].x);
             ans.y += tp * (pt[i].y + pt[nt].y);
         }
         ans.x /=  * area;
         ans.y /=  * area;
         return ans;
     }
     //判断点是否在任意多边形内[射线法]，O(n)
     bool ahas( Point &_Off)
     {
         int ret = ;
         double infv = 1e20;//坐标系最大范围
         Line l = Line( _Off, Point( -infv ,_Off.y));
         for(int i = ; i < n; i ++)
         {
             Line ln = Line( pt[i], pt[(i + ) % n]);
             if(fabs(ln.s.y - ln.e.y) > eps)
             {
                 Point tp = (ln.s.y > ln.e.y)? ln.s: ln.e;
                 if( ( fabs( tp.y - _Off.y) < eps && tp.x < _Off.x + eps) || Line::isCrossSS( ln, l))
                     ret++;
             }
             else if( Line::isCrossSS( ln, l))
                 ret++;
         }
         return ret&;
     }

     //判断任意点是否在凸包内，O(logn)
     bool bhas( Point & p)
     {
         if( n < )
             return false;
         if( xmult( pt[], p, pt[]) > eps)
             return false;
         if( xmult( pt[], p, pt[n-]) < -eps)
             return false;
         int l = ,r = n-;
         int line = -;
         while( l <= r)
         {
             int mid = ( l + r) >> ;
             if( xmult( pt[], p, pt[mid]) >= )
                 line = mid,r = mid - ;
             else l = mid + ;
         }
         return xmult( pt[line-], p, pt[line]) <= eps;
     }

     //凸多边形被直线分割
     Polygon split( Line &_Off)
     {
         //注意确保多边形能被分割
         Polygon ret;
         Point spt[];
         double tp = 0.0, np;
         bool flag = true;
         int i, pn = , spn = ;
         for(i = ; i < n; i ++)
         {
             if(flag)
                 pt[pn ++] = pt[i];
             else
                 ret.pt[ret.n ++] = pt[i];
             np = xmult( _Off.s, _Off.e, pt[(i + ) % n]);
             if(tp * np < -eps)
             {
                 flag = !flag;
                 Line::crossLPt( _Off, Line(pt[i], pt[(i + ) % n]), spt[spn++]);
             }
             tp = (fabs(np) > eps)?np: tp;
         }
         ret.pt[ret.n ++] = spt[];
         ret.pt[ret.n ++] = spt[];
         n = pn;
         return ret;
     }

     /** 卷包裹法求点集凸包，_p为输入点集，_n为点的数量 **/
     void ConvexClosure( Point _p[], int _n)
     {
         sort( _p, _p + _n);
         n = ;
         for(int i = ; i < _n; i++)
         {
             while( n >  && sgn( xmult( pt[n-], pt[n-], _p[i]), ) <= )
                 n--;
             pt[n++] = _p[i];
         }
         int _key = n;
         for(int i = _n - ; i >= ; i--)
         {
             while( n > _key && sgn( xmult( pt[n-], pt[n-], _p[i]), ) <= )
                 n--;
             pt[n++] = _p[i];
         }
         if(n>)   n--;//除去重复的点，该点已是凸包凸包起点
     }
     /****** 寻找凸包的graham 扫描法********************/
     /****** _p为输入的点集,_n为点的数量****************/

     void graham( Point _p[], int _n)
     {
         int cur=;
         for(int i = ; i < _n; i++)
             if( sgn( _p[cur].y, _p[i].y) >  || ( sgn( _p[cur].y, _p[i].y) ==  && sgn( _p[cur].x, _p[i].x) > ) )
                 cur = i;
         swap( _p[cur], _p[]);
         n = , gsort = pt[n++] = _p[];
         if( _n <= )   return;
         sort( _p + , _p+_n ,gcmp);
         pt[n++] = _p[];
         for(int i = ; i < _n; i++)
         {
             while(n> && sgn( xmult( pt[n-], pt[n-], _p[i]), ) <= )// 当凸包退化成直线时需特别注意n
                 n--;
             pt[n++] = _p[i];
         }
     }
     //凸包旋转卡壳(注意点必须顺时针或逆时针排列)
     //返回值凸包直径的平方（最远两点距离的平方）
     pair<Point,Point> rotating_calipers()
     {
         int i =  % n;
         double ret = 0.0;
         pt[n] = pt[];
         pair<Point,Point>ans=make_pair(pt[],pt[]);
         for(int j = ; j < n; j ++)
         {
             while( fabs( xmult( pt[i+], pt[j], pt[j + ])) > fabs( xmult( pt[i], pt[j], pt[j + ])) + eps)
                 i = (i + ) % n;
             //pt[i]和pt[j],pt[i + 1]和pt[j + 1]可能是对踵点
             if(ret < getdis2(pt[i],pt[j]))  ret = getdis2(pt[i],pt[j]), ans = make_pair(pt[i],pt[j]);
             if(ret < getdis2(pt[i+],pt[j+]))  ret = getdis(pt[i+],pt[j+]), ans = make_pair(pt[i+],pt[j+]);
         }
         return ans;
     }

     //凸包旋转卡壳(注意点必须逆时针排列)
     //返回值两凸包的最短距离
     double rotating_calipers( Polygon &_Off)
     {
         int i = ;
         double ret = 1e10;//inf
         pt[n] = pt[];
         _Off.pt[_Off.n] = _Off.pt[];
         //注意凸包必须逆时针排列且pt[0]是左下角点的位置
         while( _Off.pt[i + ].y > _Off.pt[i].y)
             i = (i + ) % _Off.n;
         for(int j = ; j < n; j ++)
         {
             double tp;
             //逆时针时为 >,顺时针则相反
             while((tp = xmult(_Off.pt[i + ],pt[j], pt[j + ]) - xmult(_Off.pt[i], pt[j], pt[j + ])) > eps)
                 i = (i + ) % _Off.n;
             //(pt[i],pt[i+1])和(_Off.pt[j],_Off.pt[j + 1])可能是最近线段
             ret = min(ret, Line(pt[j], pt[j + ]).dis(_Off.pt[i], true));
             ret = min(ret, Line(_Off.pt[i], _Off.pt[i + ]).dis(pt[j + ], true));
             if(tp > -eps)//如果不考虑TLE问题最好不要加这个判断
             {
                 ret = min(ret, Line(pt[j], pt[j + ]).dis(_Off.pt[i + ], true));
                 ret = min(ret, Line(_Off.pt[i], _Off.pt[i + ]).dis(pt[j], true));
             }
         }
         return ret;
     }

     //-----------半平面交-------------
     //复杂度:O(nlog2(n))
     //获取半平面交的多边形（多边形的核）
     //参数：向量集合[l]，向量数量[ln];(半平面方向在向量左边）
     //函数运行后如果n[即返回多边形的点数量]为0则不存在半平面交的多边形（不存在区域或区域面积无穷大）
     int judege( Line &_lx, Line &_ly, Line &_lz)
     {
         Point tmp;
         Line::crossLPt(_lx,_ly,tmp);
         return sgn(xmult(_lz.s,tmp,_lz.e),);
     }
     int halfPanelCross(Line L[], int ln)
     {
         int i, tn, bot, top;
         for(int i = ; i < ln; i++)
             L[i].get_angle();
         sort(L, L + ln);
         //平面在向量左边的筛选
         for(i = tn = ; i < ln; i ++)
             if(fabs(L[i].angle - L[i - ].angle) > eps)
                 L[tn ++] = L[i];
         ln = tn, n = , bot = , top = ;
         dq[] = L[], dq[] = L[];
         for(i = ; i < ln; i ++)
         {
             while(bot < top &&  judege(dq[top],dq[top-],L[i]) > )
                 top --;
             while(bot < top &&  judege(dq[bot],dq[bot+],L[i]) > )
                 bot ++;
             dq[++ top] = L[i];
         }
         while(bot < top && judege(dq[top],dq[top-],dq[bot]) > )
             top --;
         while(bot < top && judege(dq[bot],dq[bot+],dq[top]) > )
             bot ++;
         //若半平面交退化为点或线
         //        if(top <= bot + 1)
         //            return 0;
         dq[++top] = dq[bot];
         for(i = bot; i < top; i ++)
             Line::crossLPt(dq[i],dq[i + ],pt[n++]);
         return n;
     }
 };

 Polygon pa,pb;

 int main(void)
 {
     while(~scanf("%d%d",&pa.n,&pb.n)&&(pa.n||pb.n))
     {
         for(int i=;i<pa.n;i++)
             scanf("%lf%lf",&pa.pt[i].x,&pa.pt[i].y);
         for(int i=;i<pb.n;i++)
             scanf("%lf%lf",&pb.pt[i].x,&pb.pt[i].y);
         printf("%.5f\n",pa.rotating_calipers(pb));
     }
     return ;
 }