LCS 最长公共子序列

区别最长公共子串（连续）

 '''
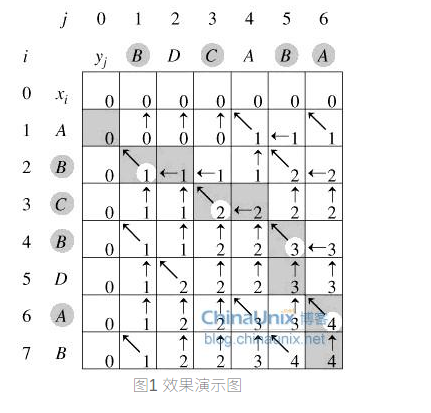
 LCS 最长公共子序列
 '''

 def LCS_len(x, y):
     m = len(x)
     n = len(y)
     dp = [[0] * (n + 1) for i in range(m + 1)]
     B = [[' '] * (n + 1) for i in range(m + 1)]
     for i in range(1, m + 1):
         for j in range(1, n + 1):
             if x[i - 1] == y[j - 1]:
                 dp[i][j] = dp[i - 1][j - 1] + 1
                 B[i][j] = 'X'
             elif dp[i - 1][j] > dp[i][j - 1]:
                 dp[i][j] = dp[i - 1][j]
                 B[i][j] = 'L'
             else:
                 dp[i][j] = dp[i][j - 1]
                 B[i][j] = 'T'
     print(dp)
     return dp, B

 def LCS_str(B, x, i, j):
     if i == 0 or j == 0:
         return
     if B[i][j] == 'X':
         print(x[i - 1])
         LCS_str(B, x, i - 1, j - 1)

     elif B[i][j] == 'L':
         LCS_str(B, x, i - 1, j)
     else:
         LCS_str(B, x, i, j - 1)

 def main():
     x = 'ABDC'
     y = 'AFBC'
     dp, B = LCS_len(x, y)
     LCS_str(B, x, len(x), len(y))
 main()