逆元-P3811 【模板】乘法逆元-洛谷luogu

https://www.cnblogs.com/zjp-shadow/p/7773566.html

------------------------------------------------------------------------------------------------------------------

乘法逆元

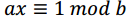
转化为

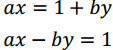
　解法：

1.exgcd

2.费马小定理（模数为质数的时候）

　　a^{p-1}=1 (mod p)

　　那么 a*a^{p-2}=1 (mod p)

3.线性递推求逆元

-----------------------------------------------------------------------------------------------------------------

乘法逆元的作用：

　　乘法逆元在模素数意义下是唯一的

　　主要用于模意义下的除法，除一个数，等于乘这个数的乘法逆元

　　注意：模数不是素数的话，假如a与模数互质，则有逆元，否则没有逆元

-----------------------------------------------------------------------------------------------------------------

题目背景

这是一道模板题

题目描述

给定n,p求1~n中所有整数在模p意义下的乘法逆元。

输入输出格式

输入格式：

一行n,p

输出格式：

n行,第i行表示i在模p意义下的逆元

输入输出样例

输入样例#1：

10 13

输出样例#1：

1
7
9
10
8
11
2
5
3
4
 
--------------------------------------------------------------

#include<cstdio>
typedef long long ll;
using namespace std;
ll v[3000000];
int main()
{
    ll n,p;
    scanf("%lld%lld",&n,&p);
    v[1]=1;
    printf("%lld\n",v[1]);
    for(ll i=2;i<=n;i++)
    {
        v[i]=(p-p/i)*v[p%i]%p;
        printf("%lld\n",v[i]);
    }
    return 0;
 } 

注意开long long

也要注意

long long定义的格式