P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1： 复制

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1： 复制

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

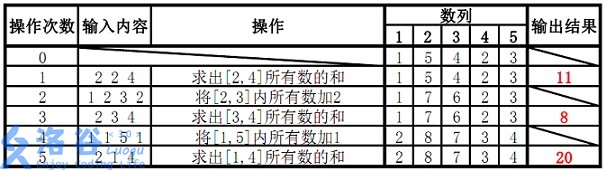
样例说明：

#include<bits/stdc++.h>
 
using namespace std;
 
const int maxn=;
 
int a[maxn+];
 
struct tree
{
    int l,r;
    long long pre,add;
}t[*maxn+];
 
void bulid(int p,int l,int r)
{
    t[p].l=l;t[p].r=r;
    if(l==r)
    {
        t[p].pre=a[l];
        return;
    }
    int mid=l+r>>;
    bulid(p*,l,mid);
    bulid(p*+,mid+,r);
    t[p].pre=t[p*].pre+t[p*+].pre;
} 
 
void spread(int p)
{
    if(t[p].add)
    {
        t[p*].pre+=t[p].add*(t[p*].r-t[p*].l+);
        t[p*+].pre+=t[p].add*(t[p*+].r-t[p*+].l+);
        t[p*].add+=t[p].add;
        t[p*+].add+=t[p].add;
        t[p].add=;
    }
}
 
void change(int p,int x,int y,int z)
{
    if(x<=t[p].l && y>=t[p].r)
    {
        t[p].pre+=(long long)z*(t[p].r-t[p].l+);
        t[p].add+=z;
        return;
    }
    spread(p);
    int mid=t[p].l+t[p].r>>;
    if(x<=mid) change(p*,x,y,z);
    if(y>mid) change(p*+,x,y,z);
    t[p].pre=t[p*].pre+t[p*+].pre;
}
 
long long ask(int p,int x,int y)
{
    if(x<=t[p].l && y>=t[p].r) return t[p].pre;
    spread(p);
    int mid=t[p].l+t[p].r>>;
    long long ans=;
    if(x<=mid) ans+=ask(p*,x,y);
    if(y>mid) ans+=ask(p*+,x,y);
    return ans;
}
 
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    scanf("%d",&a[i]);
    bulid(,,n);
    for(int i=;i<=m;i++)
    {
        int q,x,y,z;
        scanf("%d",&q);
        if(q==)
        {
            scanf("%d%d%d",&x,&y,&z);
            change(,x,y,z);
        }
        else
        {
            scanf("%d%d",&x,&y);
            cout<<ask(,x,y)<<endl;
        }
    }
    return ;
}