题解-AtCoder-agc006C Rabbit Exercise

Problem

AtCoder & bzoj

题意：数轴上有\(n\)个点（初始坐标均为整数），编号为\(1\)~\(n\)。给出\(m\)个操作。

每个操作会选定点\(a\)，然后随机在点\(a-1\)和点\(a+1\)中选一个，将点\(a\)以选中的点为中心做对称，将这\(m\)个操作按顺序执行\(k\)遍（\(1\)~\(m\)完整执行一次算\(1\)遍），求最终每个点的位置的期望值

Solution

不难发现根据期望的线性型，在\(a-1\)和\(a+1\)之间随机选一个进行对称操作的期望等价于在\(a-1\)和\(a+1\)的中点处进行对称

则我们发现，对于点\(B\)在点\(A\)和\(C\)之间，若\(A\)到\(B\)距离为\(a\)，若\(B\)到\(C\)距离为\(b\)，则对称后的位置\(B'\)与\(A\)距离为\(b\)，与\(C\)距离为\(a\)（如下图）

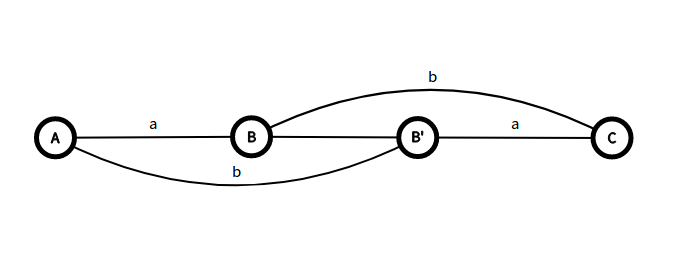
发现如果我们用一个差分数组\(d_i=a_{i+1}-a_i\)存下\(a_i\)数组的话，对称操作相当于交换\(d_i,d_{i+1}\)

发现进行一轮操作后，整个序列会成为若干个对换环（一个对换环相当于将整个环旋转一格再重新赋值），而进行\(k\)次操作相当于将所有环旋转\(k\)格

发现如果整个环的大小为\(c\)，则环旋转\(k\)次和旋转\(k\bmod c\)次是等价的，则复杂度与\(k\)无关，整体复杂度\(O(n+m)\)

Code

#include <algorithm>
#include <cstdio>
#include <cctype>
using namespace std;
typedef long long ll;
#define rg register

template <typename _Tp> inline _Tp read(_Tp&x){
	char c11=getchar(),ob=0;x=0;
	while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')ob=1,c11=getchar();
	while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;return x;
}

const int N=101000;
int a[N],vis[N],st[N];
ll b[N],p[N],k;
int n,m,tp;

void init();void work();void print();
int main(){init();work();print();return 0;}

void work(){
	int x;
	for(rg int i=1;i<=m;++i)read(x),swap(a[x],a[x+1]);
	for(rg int i=1;i<=n;++i)if(!vis[i]){
		vis[st[0]=x=i]=tp=1;
		while(!vis[a[x]])
			vis[st[tp++]=x=a[x]]=1;
		int e=k%tp;
		for(rg int j=0;j<tp;++j)
			b[st[j]]=p[st[j+e<tp?j+e:j+e-tp]];
	}
}

void print(){
	ll sm(0ll);
	for(rg int i=1;i<=n;++i)
		printf("%lld\n",sm+=b[i]);
}

void init(){
	read(n);
	for(rg int i=1;i<=n;++i)read(p[i]),a[i]=i;
	for(rg int i=n;i;--i)p[i]-=p[i-1];
	read(m),read(k);
}