Power Spectral Density

对于一个特定的信号来说，有时域与频域两个表达形式，时域表现的是信号随时间的变化，频域表现的是信号在不同频率上的分量。在信号处理中，通常会对信号进行傅里叶变换得到该信号的频域表示，从而得到信号在频域上的特性，进而可以对该信号进行频域上的处理。不过对于随机过程这种不确定的信号是无法直接进行傅里叶转换的，那么是否就意味着我们无法知晓随机过程的频域特性呢？

对于随机过程，我们也是有办法得到其频域特性的，其频域特性可以用PSD来表达。我们下面将讨论WSS Process的PSD是如何表达出其频域特性的。

Definition

如果把随机过程$x(t)$看作是单位电阻上的电压，那么$x^2(t)$则表示的是瞬时功率（能量）。当$x(t)$是WSS时，$x(t)$的瞬时功率期望$E[x^2(t)]$是固定值，期望值为

$\begin{align*}E[x^2(t)] = R_{xx}(0)
&= \mathcal{F}^{-1}\{S_{xx}(j\omega)\}(0)\\
&= \frac{1}{2\pi}\int_{-\infty}^{\infty}S_{xx}(j\omega)e^{j\omega 0}d\omega\\
&= \frac{1}{2\pi}\int_{-\infty}^{\infty}S_{xx}(j\omega)d\omega
\end{align*}$

其中随机变量的correlation，即$R_{xx}(\tau)$，是一个固定函数，因此它具有傅里叶变换$S_{xx}(j\omega)$，$\omega$就是频率。对于这个式子，我们可以这么理解：$S_{xx}(j\omega)$表示了功率（能量）期望值$E[x^2(t)]$在频域上的分布状况，宽度为$d\omega$的频率所蕴含的能量大小为$\frac{1}{2\pi}S_{xx}(j\omega)dw$。在所有的$\omega$上都有$S_{xx}(j\omega)>0$。

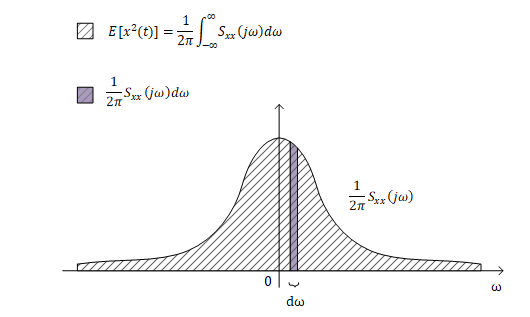
因此$S_{xx}(j\omega)$被称为Power Spectral Density（PSD）。

WSS Process Spectral Processing

通过PSD我们可以得到随机过程的频域特性，而获得频域特性的目的是为了对信号进行频域处理而服务的，接下来就需要验证这个频域特性是否满足频域处理的需求。

考虑WSS Process通过一个理想带通滤波器，得到的输出为$y(t)$，该输出process的瞬时功率期望为

$\displaystyle{E[y^2(t)] = R_{yy}(0) = \frac{1}{2\pi}\int_{-\infty}^{\infty}S_{yy}(j\omega)dw}$

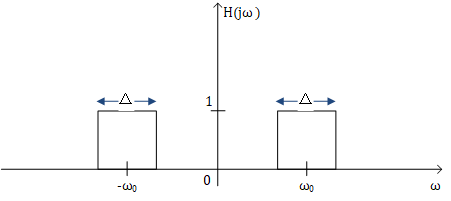
带通滤波器系统如下

带通滤波器$H(j\omega)$为实LTI系统，也就是说$H(j\omega)$是左右对称的，因此可以知道该带通滤波器在频域上有如下频谱

此外，在上一篇文章中我们讨论过WSS Process在经过LTI系统后所得的process的PSD为$S_{yy}(j\omega) = S_{xx}(j\omega)|H(j\omega)|^2$。因此$y(t)$的PSD如下图

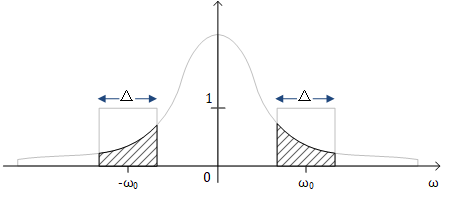
可见对WSS Process进行频域上的处理是能体现在PSD上的，这表明PSD确实能表现出WSS Process的频域特性。而PSD是auto-correlation的傅里叶变换，这表明了一个WSS Process的频域特性只与不同采样点之间的相关性有关系，跟采样点的内部PDF无关。

How to get PSD

这一小节通过Einstein-Wiener-Khinchin Theorem来引入获取PSD的方法。

假设有一WSS Process，它的一个realization为$x(t)$，我们给这个realization加上一个宽度为$2T$的窗以得到$x_T(t)$

$x_T(t) = w_T(t)x(t)$

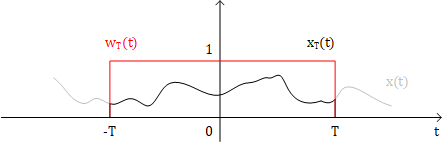
$x(t)$是实信号，那么根据傅里叶变换的共轭性质，可以得到

$\begin{align*} x_T(\tau)&\stackrel{\mathcal{F}}{\longleftrightarrow}X_T(j\omega)\\
x_{\overleftarrow{T}}(\tau) = x_T(-\tau)&\stackrel{\mathcal{F}}{\longleftrightarrow}X_T^*(j\omega) \end{align*}$

因此有

$\color{red}{x_T(\tau)*x_{\overleftarrow{T}}(\tau)}\stackrel{\mathcal{F}}{\longleftrightarrow}\color{blue}{|X_T(j\omega)|^2}$

$x(t)$是WSS process的一个realization，不过如果我们把它当作该WSS process，就可以对上述式子的两边都求期望，其中左边为

$\color{red}{\begin{align*}
E\Big\{x_T(\tau)*x_{\overleftarrow{T}}(\tau)\Big\}
&= E\left\{\int_{-\infty}^{\infty}x_T(\alpha)x_{\overleftarrow{T}}(\tau-\alpha)d\alpha\right\}\\
&= E\left\{\int_{-\infty}^{\infty}x_T(\alpha)x_T(\alpha-\tau)d\alpha\right\}\\
&= E\left\{\int_{-\infty}^{\infty}w_T(\alpha)x(\alpha)w_T(\alpha-\tau)x(\alpha-\tau)d\alpha\right\}\\
&= \int_{-\infty}^{\infty}E\Big\{x(\alpha)x(\alpha-\tau)\Big\}\cdot w_T(\alpha)w_T(\alpha-\tau)d\alpha\\
&= \int_{-\infty}^{\infty}R_{xx}(\tau)\cdot w_T(\alpha)w_T(\alpha-\tau)d\alpha\\
&= R_{xx}(\tau)\cdot 2T\Lambda(\tau)
\end{align*}}$

$\Lambda(\tau)$是一个三角形函数，顶点为$(0,1),(-T,0),(T,0)$，极限情况下有$\displaystyle{\lim_{T\to\infty}\Lambda(\tau)=1}$

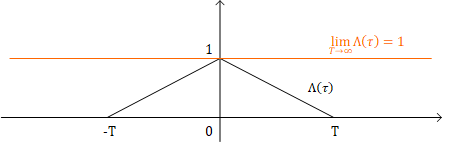
时域与频域都乘以$\frac{1}{2T}$，可以得到

$\displaystyle{\color{red}{R_{xx}(\tau)\Lambda(\tau)} \stackrel{\mathcal{F}}{\longleftrightarrow} \color{blue}{\frac{1}{2T}E\big[|X_T(j\omega)|^2\big]}}$

此时令$T\to\infty$，左边就只剩下$R_{xx}(\tau)$，它的傅里叶变换就是$S_{xx}(j\omega)$，因此得到

$\displaystyle{\color{red}{R_{xx}(\tau)} \stackrel{\mathcal{F}}{\longleftrightarrow}\color{blue}{S_{xx}(j\omega)=\lim_{T\to\infty} \frac{1}{2T}E\big[|X_T(j\omega)|^2\big]}}$

上面的式子可以这样解释：为了得到$S_{xx}(j\omega)$需要执行以下步骤

1. 获取WSS process的多个realization，这些realization的有效范围为$(-T,T)$
2. 对每个realization执行$\mathcal{F}\big\{ x_T(t)*x_{\overleftarrow{T}}(\tau) \big\}$以得到多个$|X_T(j\omega)|^2$
3. 对这些$|X_T(j\omega)|^2$求平均，然后再乘以$\frac{1}{2T}$，就能得到$S_{xx}(j\omega)$

※realization的数量越多，$T$的范围越大，最终得到的$S_{xx}(j\omega)$就会越精确。

Reference:

Alan V. Oppenheim: Signals, Systems and Inference, Chapter 10:Power Spectral Density