C#设计模式（12）——组合模式

1.组合模式

　　在软件开发中我们经常会遇到处理部分与整体的情况，如我们经常见到的树形菜单，一个菜单项的子节点可以指向具体的内容，也可以是子菜单。类似的情况还有文件夹，文件夹的下级可以是文件夹也可以是文件。举一个例子：一个公司的组织架构是这样的，首先是总公司，总公司下边有直属员工和各个部门，各个部门下边有本部门的子部门和员工。我们去怎么去获取这个公司的组织架构呢（就是有层次地遍历出公司的部门名和员工名）？

　　组合模式可以很好地解决这类问题，组合模式通过让树形结构的叶子节点和树枝节点使用同样的接口，结合递归的思想来处理部分与整体关系，这种方式模糊了简单对象（叶子）和对象组（树枝）间的概念，让我们可以像处理单个对象一样去处理对象组。

树叶和树枝都要使用相同的接口，所以先创建一个抽象类，其内部定义了树枝和树叶的公共接口：

    /// <summary>
    /// 抽象部件 定义了树枝和树叶的公共属性和接口
    /// </summary>
   public abstract class Component
    {
        public string name;
        public Component(string name)
        {
            this.name = name;
        }
        //添加子节点
        public abstract void Add(Component c);
        //删除子节点
        public abstract void Remove(Component c);
        //展示方法，dept为节点深度
        public abstract void Display(int dept);
    }

员工类，相当于树叶，没有下一级：

    //具体员工，树形结构的Leaf
    public class Employee : Component
    {
        public Employee(string name):base(name)
        {
            this.name = name;
        }
        //Leaf不能添加/删除子节点所以空实现
        public override void Add(Component c)
        {
        }
        public override void Remove(Component c)
        {

        }
        public override void Display(int dept)
        {
            Console.WriteLine(new string('-', dept)+name);
        }
    }

部门类，相当于树枝，下边的节点可有有子部门，也可以有员工：

   /// <summary>
    /// 部门类，相当于树枝
    /// </summary>
    public class Depart : Component
    {
        public Depart(string name) : base(name)
        {
            this.name = name;
        }
        //添加子节点
        public List<Component> children=new List<Component>();
        public override void Add(Component c)
        {
            children.Add(c);
        }
        //删除子节点
        public override void Remove(Component c)
        {
            children.Remove(c);
        }
        //展示自己和和内部的所有子节点，这里是组合模式的核心
        public override void Display(int dept)
        {
            Console.WriteLine(new string('-',dept)+name);
            foreach (var item in children)
            {
                //这里用到了递归的思想
                item.Display(dept + );
            }
        }
    }

客户端调用：

    class Program
    {
        static void Main(string[] args)
        {
            Component DepartA = new Depart("A总公司");
            Component DepartAX = new Depart("AX部门");
            Component DepartAY = new Depart("AY部门");
            Component DepartAX1 = new Depart("AX1子部门");
            Component DepartAX2 = new Depart("AX2子部门");
            Component Ae1 = new Employee("公司直属员工1");
            Component AXe1= new Employee("AX部门员工1");
            Component AX1e1= new Employee("AX1部门员工1");
            Component AX1e2= new Employee("AX1部门员工2");
            Component AYe1= new Employee("AY部门员工1");
            Component AYe2= new Employee("AY部门员工2");
            DepartA.Add(Ae1);
            DepartA.Add(DepartAX);
            DepartA.Add(DepartAY);
            DepartAX.Add(AXe1);
            DepartAX.Add(DepartAX1);
            DepartAX.Add(DepartAX2);
            DepartAX1.Add(AX1e1);
            DepartAX1.Add(AX1e2);
            DepartAY.Add(AYe1);
            DepartAY.Add(AYe2);
            //遍历总公司
            DepartA.Display();
            Console.ReadKey();
        }
    }

运行结果如下：

上边的例子中部门类中包含了一个List children,这个List内部装的是该部门的子节点，这些子节点可以是子部门也可以是员工，在部门类的Display方法中通过foreach来遍历每一个子节点，如果子节点是员工则直接调用员工类中的Display方法打印出名字；如果子节点是子部门，调用部门类的Display遍历子部门的下级节点，直到下级节点只有员工或者没有下级节点为止。这里用到了递归的思想。

2.小结

上边例子的类图

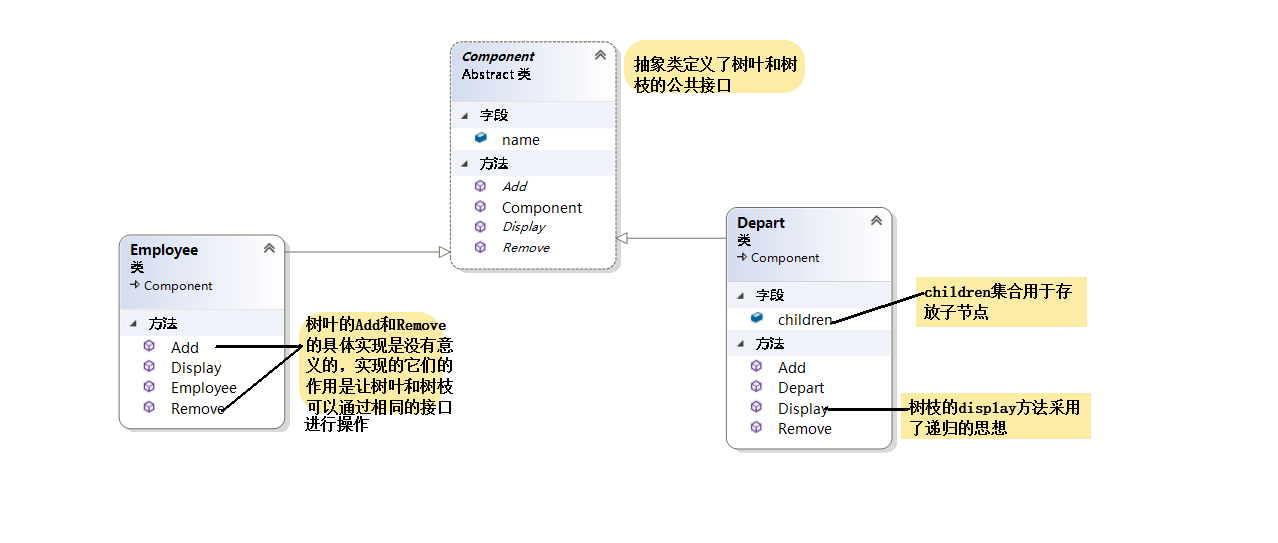
组合模式的使用场景：当我们处理部分-整体的层次结构时，希望使用统一的接口来处理部分和整体时使用。

组合模式的优点:在树形结构的处理中模糊了对象和对象组的概念，使用对象和对象组采用了统一的接口，让我们可以像处理简单对象一样处理对象组。