angular学习一框架结构认识
angular学习所有内容均会与vue以及react框架进行对比。
angular学习使用的编译器:webstorm
解决编译器屏蔽node_modules包问题:
File-->settings-->File types-->最下面
添加如下:

angular根目录文件夹结构:
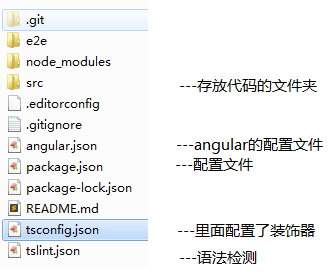
react根目录文件结构:
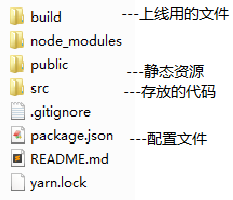
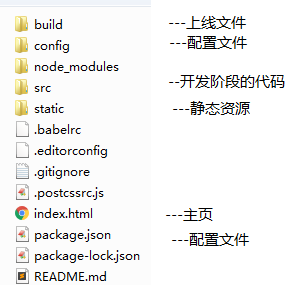
vue根目录文件结构:
angular学习一框架结构认识的更多相关文章
- angular学习资源
angular学习资源 angularjs库: https://developers.google.com/speed/libraries/devguide?hl=zh-CN#angularjs ...
- angular学习笔记(三十一)-$location(2)
之前已经介绍了$location服务的基本用法:angular学习笔记(三十一)-$location(1). 这篇是上一篇的进阶,介绍$location的配置,兼容各版本浏览器,等. *注意,这里介绍 ...
- angular学习笔记(三十一)-$location(1)
本篇介绍angular中的$location服务的基本用法,下一篇介绍它的复杂的用法. $location服务的主要作用是用于获取当前url以及改变当前的url,并且存入历史记录. 一. 获取url的 ...
- angular学习笔记(三十)-指令(10)-require和controller
本篇介绍指令的最后两个属性,require和controller 当一个指令需要和父元素指令进行通信的时候,它们就会用到这两个属性,什么意思还是要看栗子: html: <outer‐direct ...
- angular学习笔记(三十)-指令(7)-compile和link(2)
继续上一篇:angular学习笔记(三十)-指令(7)-compile和link(1) 上一篇讲了compile函数的基本概念,接下来详细讲解compile和link的执行顺序. 看一段三个指令嵌套的 ...
- angular学习笔记(三十)-指令(7)-compile和link(1)
这篇主要讲解指令中的compile,以及它和link的微妙的关系. link函数在之前已经讲过了,而compile函数,它和link函数是不能共存的,如果定义了compile属性又定义link属性,那 ...
- angular学习笔记(三十)-指令(6)-transclude()方法(又称linker()方法)-模拟ng-repeat指令
在angular学习笔记(三十)-指令(4)-transclude文章的末尾提到了,如果在指令中需要反复使用被嵌套的那一坨,需要使用transclude()方法. 在angular学习笔记(三十)-指 ...
- angular学习笔记(三十)-指令(5)-link
这篇主要介绍angular指令中的link属性: link:function(scope,iEle,iAttrs,ctrl,linker){ .... } link属性值为一个函数,这个函数有五个参数 ...
- angular学习笔记(三十)-指令(2)-restrice,replace,template
本篇主要讲解指令中的 restrict属性, replace属性, template属性 这三个属性 一. restrict: 字符串.定义指令在视图中的使用方式,一共有四种使用方式: 1. 元素: ...
随机推荐
- UESTC482-Charitable Exchange-bfs优先队列
#include <cstring> #include <algorithm> #include <iostream> #include <queue> ...
- HDU4624 Endless Spin 【最大最小反演】【期望DP】
题目分析: 题目是求$E(MAX_{i=1}^n(ai))$, 它等于$E(\sum_{s \subset S}{(-1)^{|s|-1}*min(s))} = \sum_{s \subset S}{ ...
- kubernetes(一)
•Kubernetes介绍 1.背景介绍 云计算飞速发展 - IaaS - PaaS - SaaS Docker技术突飞猛进 - 一次构建,到处运行 - 容器的快速轻量 - 完整的生态环境 2.什 ...
- SpringBoot 从application.yml中通过@Value读取不到属性值
package cn.exrick.xboot.mqtt; import org.eclipse.paho.client.mqttv3.*;import org.eclipse.paho.client ...
- 【BZOJ5314】[JSOI2018]潜入行动(动态规划)
[BZOJ5314][JSOI2018]潜入行动(动态规划) 题面 BZOJ 洛谷 题解 不难想到一个沙雕\(dp\),设\(f[i][j][0/1][0/1]\)表示当前点\(i\),子树中一共放了 ...
- 「SHOI2016」黑暗前的幻想乡 解题报告
「SHOI2016」黑暗前的幻想乡 sb题想不出来,应该去思考原因,而不是自暴自弃 一开始总是想着对子树做dp,但是状态压不起去,考虑用容斥消减一些条件变得好统计,结果越想越乱. 期间想过矩阵树定理, ...
- cf571B Minimization (dp)
相当于是把%k相同的位置的数分为一组,组与组之间互不干扰 然后发现一组中可以任意打乱顺序,并且一定是单调排列最好,那个值就是最大值减最小值 所以我给所有数排序以后,同一组应该选连续的一段最好 然后发现 ...
- Java 多个文件压缩下载
有时候会有多个附件一起下载的需求,这个时候最好就是打包下载了 首先下面这段代码是正常的单个下载 public void Download(@RequestParam("file_path&q ...
- [luogu1341][无序字母对]
luogu1341 思路 欧拉回路和欧拉路的裸题,首先判断是否存在欧拉路或者欧拉回路.当且仅当途中每个点的度数都为偶数时,存在欧拉回路.当且仅当图中度数为奇数的点的个数为2时,存在欧拉路.如果存在欧拉 ...
- RabbitMQ入门-队列
先建工程 下一步,输入坐标 下一步,输入工程名 先看一下最终目录 修改pom文件 <?xml version="1.0" encoding="UTF-8" ...
