[JXOI2018]守卫

嘟嘟嘟




正如某题解所说，这题很有误导性：我就一直在想凸包。

随便一个数据，就能把凸包hack掉：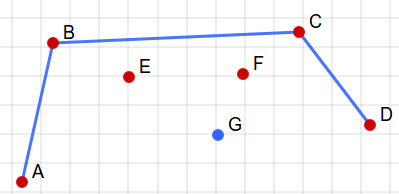

这样我们的点G就gg了。




所以正解是什么呢？dp。

题解看这位老哥的吧，我感觉挺好懂的：题解 P4563 【[JXOI2018]守卫】

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 5e3 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n;
struct Point
{
  ll x, y;
  In Point operator + (const Point& oth)const
  {
    return (Point){x + oth.x, y + oth.y};
  }
  In Point operator - (const Point& oth)const
  {
    return (Point){x - oth.x, y - oth.y};
  }
  In ll operator * (const Point& oth)const
  {
    return x * oth.y - y * oth.x;
  }
}p[maxn];

int dp[maxn][maxn];

int main()
{
  n = read();
  for(int i = 1; i <= n; ++i) p[i].x = i, p[i].y = read();
  int ans = 0;
  for(int i = 1; i <= n; ++i)
    {
      dp[i][i] = 1; ans ^= 1;
      int sum = 1, pos = 0;
      for(int j = i - 1; j; --j)
	{
	  if(!pos || (p[pos] - p[i]) * (p[j] - p[i]) < 0)
	    sum += min(dp[j + 1][pos - 1], dp[j + 1][pos]), pos = j;
	  dp[j][i] = sum + min(dp[j][pos - 1], dp[j][pos]);
	  ans ^= dp[j][i];
	}
    }
  write(ans), enter;
  return 0;
}