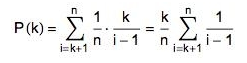[python,2018-06-29] 37%法则及其拓展解决恋爱问题

37%法则

苏格拉底的问题：

　　在一片麦田里摘出一颗最大最好的麦穗。但只能摘一次，而且不能回头。

传说这是苏格拉底给他的弟子柏拉图提出的问题，又传说柏拉图进行了2次选择：

1.柏拉图第一次走进麦田，他发现很多很好的麦穗，他摘下了他看到的第一个比较大的麦穗，然后继续往前走，却沮丧地发现自己越走越失望，前面还有不少更好的，但是他却不能再摘了。

2.柏拉图第二次走进麦田，他依然发现很多很好的麦穗，但是这一次他吸取教训——前面一定有更好的。他一直向前走，直到发现自己差不多走出了麦田。按照规则，他回不去了，而他刚刚错过了最好的麦穗。

那怎么做才能拿到最大最好的问题呢？

分析：

转化为数学问题：

　　已知在一个无序的集合 N 中（集合大小已知），一次只能查看一个数，查看后选择是否取出这个数，在只能取一次的情况下，怎么取到集合 N 中的最大数？

猜想：

　　对于这个集合，要取出最大的数， "最大"肯定是比较出来的，既然是比较，必须要有比较的对象，所以我们把集合 N 拆分为2个子集A和B，集合A用来观察和比较，

集合B用来抽取 “最大” 的数。

　　那么，该怎么拆分集合N呢？

　　想到了2种方法：

1.根据 大数定理 ，多次模拟在集合中取数，比较 取出的数 等于 集合中最大数频率，以频率估算概率。

2.遍历所有的情况，根据 全概率公式 ，进行数学计算。

解法1：

假设集合N大小为100，生成长度为100的随机数组，求出前 k 个数中的最大值 max_base，

从 k+1 开始，如果这个数大于 max_base，则取出这个数作为结果，

如果第 k+1 个数到最后都小于max_base，则取出最后一个数作为结果。

重复抽取 100000 次，以频率估算概率，

k的值为1-100，代码如下：

 # Author:shijt
 import random
 import time

 #获取数组中前 number 个数中的最大数
 def getMaxBase(number,random_list):
     return max(random_list[:number])

 def getMaxGuess(number,random_list):
     max_guess=getMaxBase(number,random_list)
     for i in range(number,100):
         if (random_list[i] >= max_guess or i==99):
             max_guess = random_list[i]
             break

     return max_guess
  for j in range(1,100):
     count = 0
     for i in range(100000):
         random_list = []
         #生成长度为100的随机数组
         for i in range(100):
             random_list.append(random.randint(1, 10000))
         if (getMaxGuess(j, random_list) == getMaxBase(100, random_list)):
             count += 1
     print(j,count, count / 100000)

以上代码重复执行了3次，得到结果

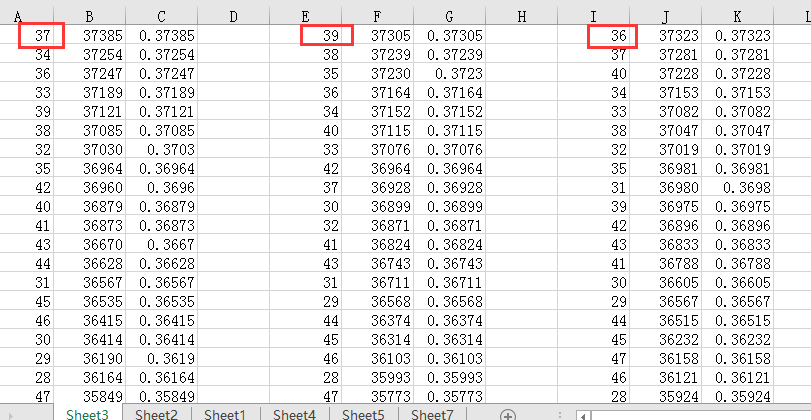
出现了3种不同的结果，分别是当k =37，39，36时，取出最大数的频率较高，都 约等于 0.373

由此猜测，当选择 37%-38%的数作为参考时，取得最大数的概率较高，约为0.373

解法2：

假设取 k 个数作为观察集合，则对于某个固定的k，第 i 个数为最大数，由全概率公式：

当n充分大时，

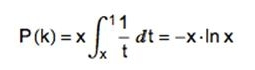
其中，x=k/n, p(k)=1,

所以，-xlnx=1,解得x=1/e,即 k/n=1/e,   e为自然对数的底

1/e约等于 0.3679,约等于37%

解后分析：

我们可以看到，解法1和解法2的结果虽然比较接近，但还是有些差别，我认为造成这个差别的原因有2个：

1.在解法二中，要求集合N足够大，而解法1中的n为 100 ，显然不能满足足够大的条件，但是由于本人计算机能力有限，仅能以此作为粗略计算；

2.当k为 35-39时，彼此之间的概率相差极小，而大数定理本身也是一种估算方法，误差难以避免。

总的来说，对于苏格拉底的问题，显然最好的方法就是 先观察前37% 的麦穗，然后再遇到比前面麦穗更大的麦穗时，就摘下，否则，则摘取最后一颗麦穗。

37%法则的拓展

有人以以上数学模型来解决 恋爱问题 ，我觉得不妥，原因有3：

1.我们不必总是找到最好的那个作为伴侣，可以接受一个相对较好的；

2.我们不能接受很差的人作为伴侣，（当只剩下一个人时，我们就没得选）；

3.我们最终是为了找到伴侣，找到比找到最好的更为重要。

问题：

　　已知在一个无序的集合 N 中（集合大小已知），一次只能查看一个数，查看后选择是否取出这个数，在只能取一次的情况下，怎么取到集合 N 中的较大数？

　　假设我们不必取到最大的数，而是以最大数的90%作为基准，大于90%则为符合需求的数，那么取得较大数的概率为多少？

分析：

我们和上面解法1一样，用大量的模拟实验来计算频率，并用频率估算概率。

解法：

 #Author:shijt
 import random
 import time

 random_list = []
 for i in range(100):
     random_list.append(random.randint(1, 10000))

 def getMaxBase(number, random_list):
     return max(random_list[:number])*0.9

 def getMaxGuess(number, random_list):
     max_guess = getMaxBase(number, random_list)
     for i in range(number,100):
         if (random_list[i] >= max_guess or i == 99):
             max_guess = random_list[i]
             break
     return max_guess

 for j in range(1,100):
     count = 0
     for i in range(10000):
         random_list = []
         for i in range(100):
             random_list.append(random.randint(1, 10000))
         if (getMaxGuess(j, random_list) >= getMaxBase(100, random_list)):
             count += 1
     print(j,count, count / 10000)

结果：

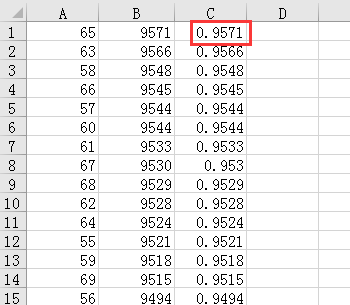
当选择63-65%的数作为参考时，可以得到 较大数 的概率较高，约等于95.7%，可以说远远高于 37%了，这才比较适合作为 恋爱问题的解法。

PS：当你愿意降低要求到85%时，你会发现，找到伴侣的概率约为 99%，还怕 找不到对象 吗？

以上仅能作为参考，毕竟人心比数学复杂的多