快速傅里叶变换（FFT）时间复杂度

图：信号在时域上和频域上的直观表示

1. 计算一维离散傅里叶变换（DFT）公式如下：

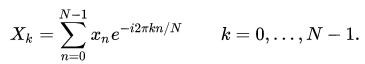
其中，N表示数据长度。由上式可知，DFT的时间复杂度是O(N*N)

2. 一维FFT的时间复杂度为O(N*logN)，其中N表示数据长度

3. 对于一个M*N的二维数据，FFT的时间复杂度为O( M*N*log(M*N) )

若M=N，则时间复杂度可以简化为O(N^2*logN)

4. 对于M维的数据（每一维长度为A，B，C，...），则FFT的时间复杂度为O( A*B*C*...* log(A*B*C*...) )

若每一维长度相同，即A=B=C=...=N，则时间复杂度可以简化为O(N^M*logN)

参考文献：

https://en.wikipedia.org/wiki/Fast_Fourier_transform

https://stackoverflow.com/questions/6514861/computational-complexity-of-the-fft-in-n-dimensions

https://stackoverflow.com/questions/12249275/computational-complexity-of-an-n-dimensional-fast-fourier-transform