最短路（bellman）-hdu1217

Dijkstra算法是处理单源最短路径的有效算法，但它局限于边的权值非负的情况，若图中出现权值为负的边，Dijkstra算法就会失效，求出的最短路径就可能是错的。

这时候，就需要使用其他的算法来求解最短路径，Bellman-Ford算法就是其中最常用的一个。

由于此题中需要求的是有一种货币A，通过一系列的转化，能够再次转化回A，因此，运用bellman算法来解决此题。

具体的关于bellman最短路的求法请见转载博客：http://www.cnblogs.com/aiguona/p/7226533.html

题目链接：https://vjudge.net/problem/HDU-1217

题目描述：

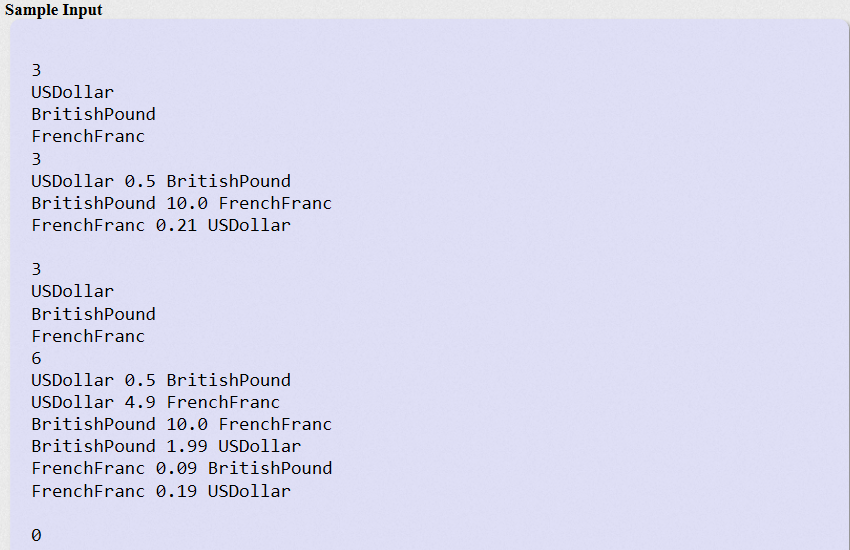
代码描述：

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <map>
#include <iostream>
using namespace std;

const int MAX_E  = ;
const int MAX_V = ;
const int INF = 0x3f3f3f3f;
struct node{
    int from,to;
    double cost;
}es[MAX_E*];//用于存图
int cae=;
int V,E;
double d[MAX_V];
map<string,int> mp;//将字符串问题转换为数字问题
bool bellman(int s){
    //fill(d,d+MAX_V,-2);
    for(int i=;i<MAX_V;i++){
        d[i]=-;
    }
    d[s]=;//是初始值为1，假设某人有1块钱，用这1块钱去做交换
    for(int j=;j<V;j++){//进行反复松弛操作，使得每个节点的最短距离估计值逐步逼近其最短距离
        bool update=false;
        for(int i=;i<E;i++){
            if(d[es[i].from]!=- && d[es[i].to] < d[es[i].from]*es[i].cost){
                if(j==V-){//当执行到V-1次循环时，说明该货币已经转换回来了
                    return true;
                }
                d[es[i].to]=d[es[i].from]*es[i].cost;
                update=true;
            }
        }
        if(!update) break;//优化这里，如果这趟没跟新任何节点就可以直接退出了。
    }
    return false;
}

void solve(){
    bool flag=false;
    for(int i=;i<V;i++){//对于每一种存在的货币来说，都遍历一遍
        if(bellman(i)){//如果说存在一种货币能够转换回来并且盈利，则成功，可直接退出
            flag=true;
            break;
        }
    }
    if(flag){
        cout << "Case " << ++cae << ": Yes" << endl;
    }else{
       cout << "Case " << ++cae << ": No" << endl;
    }
}

int main(){
    //ios::sync_with_stdio(false)的用法：详见博客  https://blog.csdn.net/vocaloid01/article/details/77892490
    ios::sync_with_stdio(false);//这样就可以取消cin于stdin的同步，使得cin的效率与scanf差不多，其中sync好像是同步的意思
    while(cin>> V && V){
        mp.clear();
        for(int i=;i<V;i++){
            string str;
            cin >> str;
            mp[str]=i;//将str的“下标”赋值为i，即为了方便后续存图，用数字i来代替字符串str
        }
        cin >> E;
        map<string,int>::iterator it;//迭代器用于遍历map中的元素
        for(int i=;i<E;i++){
            string str1,str2;
            double cost;
            cin >> str1 >> cost >> str2;
            it=mp.find(str1);//查找函数，即找到str1在mp中的位置
            es[i].from=it->second;//将找到的str1对应的“下标”，将结点i的起点值赋值为str1所对应的下标值
            it=mp.find(str2);
            es[i].to=it->second;//将找到的str2对应的“下标”，将结点i的终点值赋值为str1所对应的下标值
            es[i].cost=cost;//把结点i由起点from->to所对应的边的边长赋值为cost
        }
        solve();
    }
    return ;
}