Fantasia （Tarjan+树形DP）

Time Limit: 1000 ms   Memory Limit: 256 MB

Description

　　给定一张N个点、M条边的无向图 $G$ 。每个点有个权值Wi。

　　我们定义 $G_i$ 为图 $G$ 中删除第 $i$ 号顶点后的图。我们想计算 $G_1, G_2, ..., G_n$ 这N张图的权值。

　　对于任意一张图 $G$ ，它的权值是这样定义的：

　　1. 如果 $G$ 是联通图，那么 $G$ 的权值为 $G$ 中所有顶点权值的乘积。

　　2. 如果 $G$ 是非联通图，那么 $G$ 的权值为 $G$ 中所有联通块的权值之和。

　　$G$ 中的一个联通块指的是 $G$ 的一个子图，并且这个子图中的点两两相连（包括直接连接或者间接连接），并且不存在子图外的点使得子图内的点能与子图外的点相连。

Input

　　第一行包含两个整数 $n$ 和 $m$ $(2 \le n \le 10^5, 1 \le m \le 2 \times 10^5)$ ，分别表示点数和边数。

　　第二行包含 $n$ 个整数 $w_1, w_2, ..., w_n$ $(1 \le w_i \le 10^9)$, 表示每个顶点的权值。

　　接下来 m 行，每行两个整数 $x_i$ 和 $y_i$ $(1 \le x_i, y_i \le n, x_i \ne y_i)$, 表示一条无向边。

　　输出只有一个整数： $S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$, 其中 $z_i$ 是图 $G_i$ 的权值。

Sample Input	Sample Output
10 3 3 3 3 2 3 3 2 3 1 3 1 1 3 1 2 1 3 1 1 1 2 1 2 2 1 3 2 1 2 1	3 1 3 0 1 0 1 0 0 1

Hint

　　【数据范围及约定】

　　子任务1（5分）： $n \leq 10, m \leq 20$

　　子任务2（10分）： $n \leq 1000, m \leq 2000$

　　子任务3（20分）： 该图恰为一棵树，$m = n-1$

　　子任务4（20分）： 该图为一幅联通图

　　子任务5（45分）： 我们会拿最强的数据来评测你的程序（mmp）

　　对于所有数据，$2 \le n \le 10^5, 1 \le m \le 2 \times 10^5$

---

题解

　　没有什么能阻挡我把Tarjan打残。

　　题目涉及到删点操作。

　　如果删的点$u$是一个非割顶，那么它的消失貌似对这个联通块整体没有太大的影响，要处理的话仅仅是该当前联通块的权值$val$除去$u$的权值$w_u$。

　　如果删的点$u$是一个割顶，那么它会将这个联通块分成若干部分，具体就是在Tarjan的缩点树上，把子树全部断开，把父亲也断开。问题来了，割顶这个东西很烦怎么处理？

　

转树

　　割顶出现了！它可以同时处于多个点双内，mmp

　　对于每个点双，我们暂且新建一个代表点，将点双内的所有点连向这个代表点。这样，一个割顶可以被连接到多个点双的代表点，同时整个图转成了树的形态。

　　

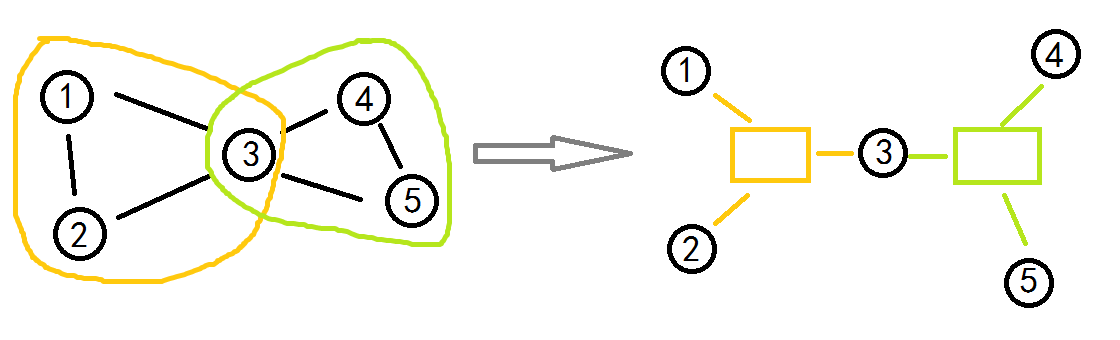
　　那么断开一个割顶$u$会影响到哪些区块，就一目了然了，即这种树上，$u$的所有子树和父亲那一头的部分。

　　发现这其实同化了断开非割顶的操作，非割顶永远处于根节点或叶子节点，其实本质上处理是一样的。

　　维护

　　$$f_u=\prod\limits_{v\in 以u为根的树}w[v]\\g_u=\sum\limits_{v是u的子树}f[v]$$

　　则删去一个点$u$，对所在联通块权值$val$的影响即为：

　　$$val=\frac{val}{f_u}+g_u$$

　   即父亲那一头的权值+所有子树的权值和

小细节与特判

　　1.处理删去割顶的时候（即上面的最后一个公式），$\frac{val}{f_u}$希望得到的是父亲那一头的权值，但如果$u$是树的根，这玩意弄出来却是1，而不是我们希望的0（坑爹），所以记录一下我们要处理的割顶是不是一个树的根，特判一下。

　   2.Tarjan深搜的起始点要记为割顶。

---

 #include <cstdio>
 #define min(a,b) (a<b?a:b)
 using namespace std;
 typedef long long ll;
 const ll N=,Mod=1e9+;
 int n,m,h1[N],h2[N*],tot;
 int col[N],colcnt,st[N],top,bcnt,head[N];
 ll info[N],sumup,ans,f[N*],g[N*],w[N*];
 int dfn[N],low[N],ins[N],tmcnt;
 bool cut[N];
 struct Edge{int v,next;}G[N*];
 inline void addEdge(int u,int v,int *h){
     G[++tot].v=v; G[tot].next=h[u]; h[u]=tot;
 }
 void tarjan(int u,int fa){
     st[++top]=u;
     ins[u]=;
     dfn[u]=low[u]=++tmcnt;
     col[u]=colcnt;
     info[col[u]]=(info[col[u]]*w[u])%Mod;
     for(int i=h1[u],v,ccnt=;i;i=G[i].next)
     if((v=G[i].v)!=fa){
         if(!ins[v]){
             ccnt++;
             tarjan(v,u);
             low[u]=min(low[u],low[v]);
             if((!fa&&ccnt>)||(fa&&dfn[u]<=low[v]))
                 cut[u]=;
             if(dfn[u]<=low[v]){
                 w[(++bcnt)+n]=;
                 do{
                     addEdge(st[top],bcnt+n,h2);
                     addEdge(bcnt+n,st[top],h2);
                     top--;
                 }while(st[top+]!=v);
                 addEdge(u,bcnt+n,h2);
                 addEdge(bcnt+n,u,h2);
             }
         }
         else if(ins[v]==)
             low[u]=min(low[u],dfn[v]);
     }
     ins[u]=;
 }
 void dfs(int u,int fa){
     f[u]=w[u]; g[u]=;
     for(int i=h2[u],v;i;i=G[i].next)
         if((v=G[i].v)!=fa){
             dfs(v,u);
             f[u]=(f[u]*f[v])%Mod;
             g[u]=(g[u]+f[v])%Mod;
         }
 }
 ll ksm(ll bas,ll tm){
     if(tm==) return ;
     ll ret=ksm(bas,tm/);
     ret=(ret*ret)%Mod;
     return ((tm&)?ret*bas:ret)%Mod;
 }
 ll inv(int x){return ksm(x,Mod-);}
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%lld",&w[i]);
     for(int i=,u,v;i<=m;i++){
         scanf("%d%d",&u,&v);
         addEdge(u,v,h1); addEdge(v,u,h1);
     }
     for(int i=;i<=n;i++)
         if(!dfn[i]){
             info[++colcnt]=;
             tarjan(i,);
             cut[i]=;
             sumup=(sumup+info[colcnt])%Mod;
             head[colcnt]=i;
             dfs(i,);
         }
     for(ll i=,k;i<=n;i++){
         int c=col[i];
         if(!cut[i])
             k=(sumup+Mod*-info[c]+(info[c]*inv(w[i]))%Mod)%Mod;
         else{
             if(head[c]!=i) k=(sumup+Mod*-info[c]+(info[c]*inv((f[i])%Mod)%Mod)%Mod+g[i])%Mod;
             else k=(sumup+Mod*-info[c]+g[i])%Mod;
         }
         ans=(ans+(i*k)%Mod)%Mod;
     }
     printf("%lld\n",ans);
     return ;
 }

奇妙代码