决策树系列（五）——CART
CART，又名分类回归树，是在ID3的基础上进行优化的决策树，学习CART记住以下几个关键点：
（1）CART既能是分类树，又能是分类树；
（2）当CART是分类树时，采用GINI值作为节点分裂的依据；当CART是回归树时，采用样本的最小方差作为节点分裂的依据；
（3）CART是一棵二叉树。
接下来将以一个实际的例子对CART进行介绍：
表1 原始数据表
|
看电视时间 |
婚姻情况 |
职业 |
年龄 |
|
3 |
未婚 |
学生 |
12 |
|
4 |
未婚 |
学生 |
18 |
|
2 |
已婚 |
老师 |
26 |
|
5 |
已婚 |
上班族 |
47 |
|
2.5 |
已婚 |
上班族 |
36 |
|
3.5 |
未婚 |
老师 |
29 |
|
4 |
已婚 |
学生 |
21 |
从以下的思路理解CART：
分类树？回归树？
分类树的作用是通过一个对象的特征来预测该对象所属的类别，而回归树的目的是根据一个对象的信息预测该对象的属性，并以数值表示。
CART既能是分类树，又能是决策树，如上表所示，如果我们想预测一个人是否已婚，那么构建的CART将是分类树；如果想预测一个人的年龄，那么构建的将是回归树。
分类树和回归树是怎么做决策的？假设我们构建了两棵决策树分别预测用户是否已婚和实际的年龄，如图1和图2所示：
图1 预测婚姻情况决策树 图2 预测年龄的决策树
图1表示一棵分类树，其叶子节点的输出结果为一个实际的类别，在这个例子里是婚姻的情况（已婚或者未婚），选择叶子节点中数量占比最大的类别作为输出的类别；
图2是一棵回归树，预测用户的实际年龄，是一个具体的输出值。怎样得到这个输出值？一般情况下选择使用中值、平均值或者众数进行表示，图2使用节点年龄数据的平均值作为输出值。
CART如何选择分裂的属性？
分裂的目的是为了能够让数据变纯，使决策树输出的结果更接近真实值。那么CART是如何评价节点的纯度呢？如果是分类树，CART采用GINI值衡量节点纯度；如果是回归树，采用样本方差衡量节点纯度。节点越不纯，节点分类或者预测的效果就越差。
GINI值的计算公式：
节点越不纯，GINI值越大。以二分类为例，如果节点的所有数据只有一个类别，则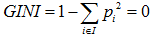
，如果两类数量相同，则
。
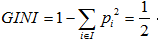回归方差计算公式：
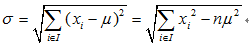
方差越大，表示该节点的数据越分散，预测的效果就越差。如果一个节点的所有数据都相同，那么方差就为0，此时可以很肯定得认为该节点的输出值；如果节点的数据相差很大，那么输出的值有很大的可能与实际值相差较大。
因此，无论是分类树还是回归树，CART都要选择使子节点的GINI值或者回归方差最小的属性作为分裂的方案。即最小化（分类树）：
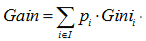
或者（回归树）：
CART如何分裂成一棵二叉树？
节点的分裂分为两种情况，连续型的数据和离散型的数据。
CART对连续型属性的处理与C4.5差不多，通过最小化分裂后的GINI值或者样本方差寻找最优分割点，将节点一分为二，在这里不再叙述，详细请看C4.5。
对于离散型属性，理论上有多少个离散值就应该分裂成多少个节点。但CART是一棵二叉树，每一次分裂只会产生两个节点，怎么办呢？很简单，只要将其中一个离散值独立作为一个节点，其他的离散值生成另外一个节点即可。这种分裂方案有多少个离散值就有多少种划分的方法，举一个简单的例子：如果某离散属性一个有三个离散值X，Y，Z，则该属性的分裂方法有{X}、{Y，Z}，{Y}、{X，Z}，{Z}、{X，Y}，分别计算每种划分方法的基尼值或者样本方差确定最优的方法。
以属性“职业”为例，一共有三个离散值，“学生”、“老师”、“上班族”。该属性有三种划分的方案，分别为{“学生”}、{“老师”、“上班族”}，{“老师”}、{“学生”、“上班族”}，{“上班族”}、{“学生”、“老师”}，分别计算三种划分方案的子节点GINI值或者样本方差，选择最优的划分方法，如下图所示：
第一种划分方法：{“学生”}、{“老师”、“上班族”}
预测是否已婚（分类）：
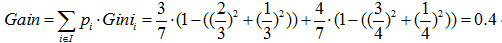
预测年龄（回归）：
第二种划分方法：{“老师”}、{“学生”、“上班族”}
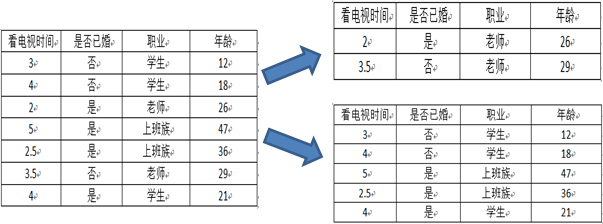
预测是否已婚（分类）：
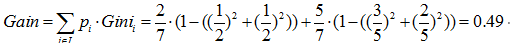
预测年龄（回归）：
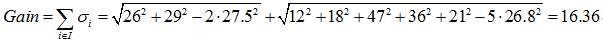
第三种划分方法：{“上班族”}、{“学生”、“老师”}
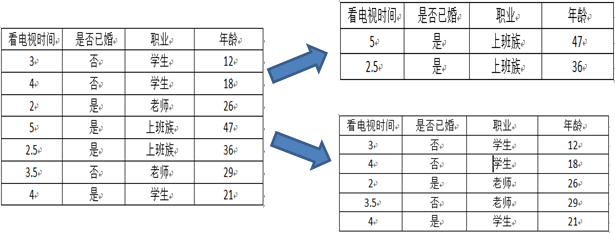
预测是否已婚（分类）：
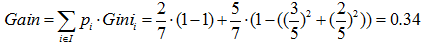
预测年龄（回归）：
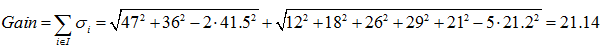
综上，如果想预测是否已婚，则选择{“上班族”}、{“学生”、“老师”}的划分方法，如果想预测年龄，则选择{“老师”}、{“学生”、“上班族”}的划分方法。
如何剪枝？
CART采用CCP（代价复杂度）剪枝方法。代价复杂度选择节点表面误差率增益值最小的非叶子节点，删除该非叶子节点的左右子节点，若有多个非叶子节点的表面误差率增益值相同小，则选择非叶子节点中子节点数最多的非叶子节点进行剪枝。
可描述如下：
令决策树的非叶子节点为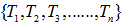
。
a）计算所有非叶子节点的表面误差率增益值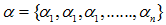
b）选择表面误差率增益值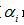
最小的非叶子节点
（若多个非叶子节点具有相同小的表面误差率增益值，选择节点数最多的非叶子节点）。
c）对
进行剪枝
表面误差率增益值的计算公式：
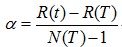
其中：
表示叶子节点的误差代价，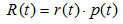
，
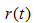为节点的错误率， 
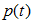为节点数据量的占比；
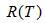表示子树的误差代价，
， 
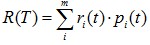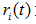为子节点i的错误率，
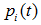表示节点i的数据节点占比；
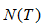表示子树节点个数。
算例：
下图是其中一颗子树，设决策树的总数据量为40。
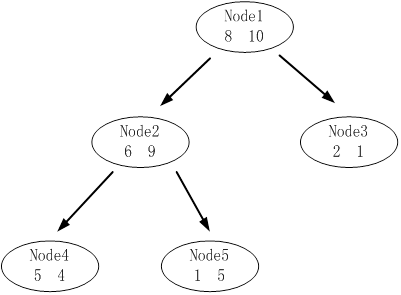
该子树的表面误差率增益值可以计算如下：
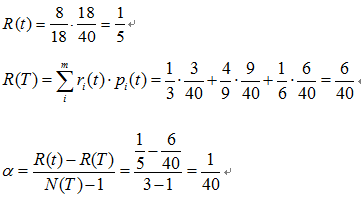
求出该子树的表面错误覆盖率为 ，只要求出其他子树的表面误差率增益值就可以对决策树进行剪枝。
程序实际以及源代码
流程图：
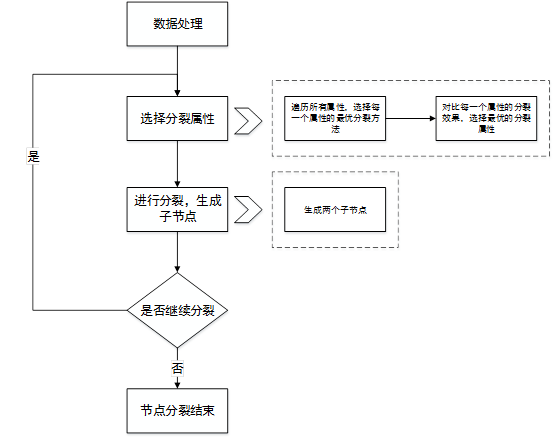
（1）数据处理
对原始的数据进行数字化处理，并以二维数据的形式存储，每一行表示一条记录，前n-1列表示属性，最后一列表示分类的标签。
如表1的数据可以转化为表2：
表2 初始化后的数据
|
看电视时间 |
婚姻情况 |
职业 |
年龄 |
|
3 |
未婚 |
学生 |
12 |
|
4 |
未婚 |
学生 |
18 |
|
2 |
已婚 |
老师 |
26 |
|
5 |
已婚 |
上班族 |
47 |
|
2.5 |
已婚 |
上班族 |
36 |
|
3.5 |
未婚 |
老师 |
29 |
|
4 |
已婚 |
学生 |
21 |
其中，对于“婚姻情况”属性，数字{1，2}分别表示{未婚，已婚 }；对于“职业”属性{1，2，3， }分别表示{学生、老师、上班族}；
代码如下所示：
static double[][] allData; //存储进行训练的数据
static List<String>[] featureValues; //离散属性对应的离散值
featureValues是链表数组，数组的长度为属性的个数，数组的每个元素为该属性的离散值链表。
（2）两个类：节点类和分裂信息
a）节点类Node
该类表示一个节点，属性包括节点选择的分裂属性、节点的输出类、孩子节点、深度等。注意，与ID3中相比，新增了两个属性：leafWrong和leafNode_Count分别表示叶子节点的总分类误差和叶子节点的个数，主要是为了方便剪枝。
class Node
{
/// <summary>
/// 每一个节点的分裂值
/// </summary>
public List<String> features { get; set; }
/// <summary>
/// 分裂属性的类型{离散、连续}
/// </summary>
public String feature_Type { get; set; }
/// <summary>
/// 分裂属性的下标
/// </summary>
public String SplitFeature { get; set; }
//List<int> nums = new List<int>(); //行序号
/// <summary>
/// 每一个类对应的数目
/// </summary>
public double[] ClassCount { get; set; }
//int[] isUsed = new int[0]; //属性的使用情况 1：已用 2:未用
/// <summary>
/// 孩子节点
/// </summary>
public List<Node> childNodes { get; set; }
Node Parent = null;
/// <summary>
/// 该节点占比最大的类别
/// </summary>
public String finalResult { get; set; }
/// <summary>
/// 树的深度
/// </summary>
public int deep { get; set; }
/// <summary>
/// 最大的类下标
/// </summary>
public int result { get; set; }
/// <summary>
/// 子节点误差
/// </summary>
public int leafWrong { get; set; }
/// <summary>
/// 子节点数目
/// </summary>
public int leafNode_Count { get; set; }
/// <summary>
/// 数据量
/// </summary>
public int rowCount { get; set; } public void setClassCount(double[] count)
{
this.ClassCount = count;
double max = ClassCount[];
int result = ;
for (int i = ; i < ClassCount.Length; i++)
{
if (max < ClassCount[i])
{
max = ClassCount[i];
result = i;
}
}
this.result = result;
}
public double getErrorCount()
{
return rowCount - ClassCount[result];
}
}
树的节点
b）分裂信息类，该类存储节点进行分裂的信息，包括各个子节点的行坐标、子节点各个类的数目、该节点分裂的属性、属性的类型等。
class SplitInfo
{
/// <summary>
/// 分裂的属性下标
/// </summary>
public int splitIndex { get; set; }
/// <summary>
/// 数据类型
/// </summary>
public int type { get; set; }
/// <summary>
/// 分裂属性的取值
/// </summary>
public List<String> features { get; set; }
/// <summary>
/// 各个节点的行坐标链表
/// </summary>
public List<int>[] temp { get; set; }
/// <summary>
/// 每个节点各类的数目
/// </summary>
public double[][] class_Count { get; set; }
}
分裂信息
主方法findBestSplit(Node node,List<int> nums,int[] isUsed)，该方法对节点进行分裂
其中：
node表示即将进行分裂的节点；
nums表示节点数据对一个的行坐标列表；
isUsed表示到该节点位置所有属性的使用情况；
findBestSplit的这个方法主要有以下几个组成部分：
1）节点分裂停止的判定
节点分裂条件如上文所述，源代码如下：
public static bool ifEnd(Node node, double shang,int[] isUsed)
{
try
{
double[] count = node.ClassCount;
int rowCount = node.rowCount;
int maxResult = ;
double maxRate = ;
#region 数达到某一深度
int deep = node.deep;
if (deep >= )
{
maxResult = node.result + ;
node.feature_Type="result";
node.features=new List<String>() { maxResult + "" };
node.leafWrong=rowCount - Convert.ToInt32(count[maxResult-]);
node.leafNode_Count=;
return true;
}
#endregion
#region 纯度(其实跟后面的有点重了，记得要修改)
//maxResult = 1;
//for (int i = 1; i < count.Length; i++)
//{
// if (count[i] / rowCount >= 0.95)
// {
// node.feature_Type="result";
// node.features=new List<String> { "" + (i + ) };
// node.leafNode_Count=1;
// node.leafWrong=rowCount - Convert.ToInt32 (count[i]);
// return true;
// }
//}
#endregion
#region 熵为0
if (shang == )
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type="result";
node.features=new List<String> { maxResult + "" };
node.leafWrong=rowCount - Convert.ToInt32(count [maxResult - ]);
node.leafNode_Count=;
return true;
}
#endregion
#region 属性已经分完
//int[] isUsed = node.getUsed();
bool flag = true;
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
flag = false;
break;
}
}
if (flag)
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count [maxResult - ]));
node.leafNode_Count=();
return true;
}
#endregion
#region 几点数少于100
if (rowCount < Limit_Node)
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type="result";
node.features=new List<String> { "" + (maxResult) };
node.leafWrong=rowCount - Convert.ToInt32(count [maxResult - ]);
node.leafNode_Count=;
return true;
}
#endregion
return false;
}
catch (Exception e)
{
return false;
}
}
停止分裂的条件
2）寻找最优的分裂属性
寻找最优的分裂属性需要计算每一个分裂属性分裂后的GINI值或者样本方差，计算公式上文已给出，其中GINI值的计算代码如下：
public static double getGini(double[] counts, int countAll)
{
double Gini = ;
for (int i = ; i < counts.Length; i++)
{
Gini = Gini - Math.Pow(counts[i] / countAll, );
}
return Gini;
}
GINI值计算
3）进行分裂，同时对子节点进行迭代处理
其实就是递归的过程，对每一个子节点执行findBestSplit方法进行分裂。
findBestSplit源代码：
public static Node findBestSplit(Node node,List<int> nums,int[] isUsed)
{
try
{
//判断是否继续分裂
double totalShang = getGini(node.ClassCount, node.rowCount);
if (ifEnd(node, totalShang, isUsed))
{
return node;
}
#region 变量声明
SplitInfo info = new SplitInfo();
info.initial();
int RowCount = nums.Count; //样本总数
double jubuMax = ; //局部最大熵
int splitPoint = ; //分裂的点
double splitValue = ; //分裂的值
#endregion
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
continue;
}
#region 离散变量
if (type[i] == )
{
double[][] allCount = new double[allNum[i]][];
for (int j = ; j < allCount.Length; j++)
{
allCount[j] = new double[classCount];
}
int[] countAllFeature = new int[allNum[i]];
List<int>[] temp = new List<int>[allNum[i]];
double[] allClassCount = node.ClassCount; //所有类别的数量
for (int j = ; j < temp.Length; j++)
{
temp[j] = new List<int>();
}
for (int j = ; j < nums.Count; j++)
{
int index = Convert.ToInt32(allData[nums[j]][i]);
temp[index - ].Add(nums[j]);
countAllFeature[index - ]++;
allCount[index - ][Convert.ToInt32(allData[nums[j]][lieshu - ]) - ]++;
}
double allShang = ;
int choose = ; double[][] jubuCount = new double[][];
for (int k = ; k < allCount.Length; k++)
{
if (temp[k].Count == )
continue;
double JubuShang = ;
double[][] tempCount = new double[][];
tempCount[] = allCount[k];
tempCount[] = new double[allCount[].Length];
for (int j = ; j < tempCount[].Length; j++)
{
tempCount[][j] = allClassCount[j] - allCount[k][j];
}
JubuShang = JubuShang + getGini(tempCount[], countAllFeature[k]) * countAllFeature[k] / RowCount;
int nodecount = RowCount - countAllFeature[k];
JubuShang = JubuShang + getGini(tempCount[], nodecount) * nodecount / RowCount;
if (JubuShang < allShang)
{
allShang = JubuShang;
jubuCount = tempCount;
choose = k;
}
}
if (allShang < jubuMax)
{
info.type = ;
jubuMax = allShang;
info.class_Count = jubuCount;
info.temp[] = temp[choose];
info.temp[] = new List<int>();
info.features = new List<string>();
info.features.Add((choose + ) + "");
info.features.Add("");
for (int j = ; j < temp.Length; j++)
{
if (j == choose)
continue;
for (int k = ; k < temp[j].Count; k++)
{
info.temp[].Add(temp[j][k]);
}
if (temp[j].Count != )
{
info.features[] = info.features[] + (j + ) + ",";
}
}
info.splitIndex = i;
}
}
#endregion
#region 连续变量
else
{
double[] leftCunt = new double[classCount]; //做节点各个类别的数量
double[] rightCount = new double[classCount]; //右节点各个类别的数量
double[] count1 = new double[classCount]; //子集1的统计量
double[] count2 = new double [node.ClassCount.Length]; //子集2的统计量
for (int j = ; j < node.ClassCount.Length; j++)
{
count2[j] = node.ClassCount[j];
}
int all1 = ; //子集1的样本量
int all2 = nums.Count; //子集2的样本量
double lastValue = ; //上一个记录的类别
double currentValue = ; //当前类别
double lastPoint = ; //上一个点的值
double currentPoint = ; //当前点的值
double[] values = new double[nums.Count];
for (int j = ; j < values.Length; j++)
{
values[j] = allData[nums[j]][i];
}
QSort(values, nums, , nums.Count - );
double lianxuMax = ; //连续型属性的最大熵
#region 寻找最佳的分割点
for (int j = ; j < nums.Count - ; j++)
{
currentValue = allData[nums[j]][lieshu - ];
currentPoint = (allData[nums[j]][i]);
if (j == )
{
lastValue = currentValue;
lastPoint = currentPoint;
}
if (currentValue != lastValue && currentPoint != lastPoint)
{
double shang1 = getGini(count1, all1);
double shang2 = getGini(count2, all2);
double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2);
//allShang = (totalShang - allShang);
if (lianxuMax > allShang)
{
lianxuMax = allShang;
for (int k = ; k < count1.Length; k++)
{
leftCunt[k] = count1[k];
rightCount[k] = count2[k];
}
splitPoint = j;
splitValue = (currentPoint + lastPoint) / ;
}
}
all1++;
count1[Convert.ToInt32(currentValue) - ]++;
count2[Convert.ToInt32(currentValue) - ]--;
all2--;
lastValue = currentValue;
lastPoint = currentPoint;
}
#endregion
#region 如果超过了局部值，重设
if (lianxuMax < jubuMax)
{
info.type = ;
info.splitIndex = i;
info.features=new List<string>() {splitValue+""};
//finalPoint = splitPoint;
jubuMax = lianxuMax;
info.temp[] = new List<int>();
info.temp[] = new List<int>();
for (int k = ; k < splitPoint; k++)
{
info.temp[].Add(nums[k]);
}
for (int k = splitPoint; k < nums.Count; k++)
{
info.temp[].Add(nums[k]);
}
info.class_Count[] = new double [leftCunt.Length];
info.class_Count[] = new double [leftCunt.Length];
for (int k = ; k < leftCunt.Length; k++)
{
info.class_Count[][k] = leftCunt[k];
info.class_Count[][k] = rightCount [k];
}
}
#endregion
}
#endregion
}
#region 没有寻找到最佳的分裂点，则设置为叶节点
if (info.splitIndex == -)
{
double[] finalCount = node.ClassCount;
double max = finalCount[];
int result = ;
for (int i = ; i < finalCount.Length; i++)
{
if (finalCount[i] > max)
{
max = finalCount[i];
result = (i + );
}
}
node.feature_Type="result";
node.features=new List<String> { "" + result };
return node;
}
#endregion
#region 分裂
int deep = node.deep;
node.SplitFeature = ("" + info.splitIndex);
List<Node> childNode = new List<Node>();
int[][] used = new int[][];
used[] = new int[isUsed.Length];
used[] = new int[isUsed.Length];
for (int i = ; i < isUsed.Length; i++)
{
used[][i] = isUsed[i];
used[][i] = isUsed[i];
}
if (info.type == )
{
used[][info.splitIndex] = ;
node.feature_Type = ("离散");
}
else
{
//used[info.splitIndex] = 0;
node.feature_Type = ("连续");
}
List<int>[] rowIndex = info.temp;
List<String> features = info.features;
Node node1 = new Node();
Node node2 = new Node();
node1.setClassCount(info.class_Count[]);
node2.setClassCount(info.class_Count[]);
node1.rowCount = info.temp[].Count;
node2.rowCount = info.temp[].Count;
node1.deep = deep + ;
node2.deep = deep + ;
node1 = findBestSplit(node1, info.temp[],used[]);
node2 = findBestSplit(node2, info.temp[], used[]);
node.leafNode_Count = (node1.leafNode_Count +node2.leafNode_Count);
node.leafWrong = (node1.leafWrong+node2.leafWrong);
node.features = (features);
childNode.Add(node1);
childNode.Add(node2);
node.childNodes = childNode;
#endregion
return node;
}
catch (Exception e)
{
Console.WriteLine(e.StackTrace);
return node;
}
}
节点选择属性和分裂
（4）剪枝
代价复杂度剪枝方法（CCP）：
public static void getSeries(Node node)
{
Stack<Node> nodeStack = new Stack<Node>();
if (node != null)
{
nodeStack.Push(node);
}
if (node.feature_Type == "result")
return;
List<Node> childs = node.childNodes;
for (int i = ; i < childs.Count; i++)
{
getSeries(node);
}
}
CCP代价复杂度剪枝
CART全部核心代码：
/// <summary>
/// 判断是否还需要分裂
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
public static bool ifEnd(Node node, double shang,int[] isUsed)
{
try
{
double[] count = node.ClassCount;
int rowCount = node.rowCount;
int maxResult = ;
double maxRate = ;
#region 数达到某一深度
int deep = node.deep;
if (deep >= )
{
maxResult = node.result + ;
node.feature_Type="result";
node.features=new List<String>() { maxResult + "" };
node.leafWrong=rowCount - Convert.ToInt32(count[maxResult-]);
node.leafNode_Count=;
return true;
}
#endregion
#region 纯度(其实跟后面的有点重了，记得要修改)
//maxResult = 1;
//for (int i = 1; i < count.Length; i++)
//{
// if (count[i] / rowCount >= 0.95)
// {
// node.feature_Type="result";
// node.features=new List<String> { "" + (i + ) };
// node.leafNode_Count=1;
// node.leafWrong=rowCount - Convert.ToInt32 (count[i]);
// return true;
// }
//}
#endregion
#region 熵为0
if (shang == )
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type="result";
node.features=new List<String> { maxResult + "" };
node.leafWrong=rowCount - Convert.ToInt32(count [maxResult - ]);
node.leafNode_Count=;
return true;
}
#endregion
#region 属性已经分完
//int[] isUsed = node.getUsed();
bool flag = true;
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
flag = false;
break;
}
}
if (flag)
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count [maxResult - ]));
node.leafNode_Count=();
return true;
}
#endregion
#region 几点数少于100
if (rowCount < Limit_Node)
{
maxRate = count[] / rowCount;
maxResult = ;
for (int i = ; i < count.Length; i++)
{
if (count[i] / rowCount >= maxRate)
{
maxRate = count[i] / rowCount;
maxResult = i + ;
}
}
node.feature_Type="result";
node.features=new List<String> { "" + (maxResult) };
node.leafWrong=rowCount - Convert.ToInt32(count [maxResult - ]);
node.leafNode_Count=;
return true;
}
#endregion
return false;
}
catch (Exception e)
{
return false;
}
}
#region 排序算法
public static void InsertSort(double[] values, List<int> arr, int StartIndex, int endIndex)
{
for (int i = StartIndex + ; i <= endIndex; i++)
{
int key = arr[i];
double init = values[i];
int j = i - ;
while (j >= StartIndex && values[j] > init)
{
arr[j + ] = arr[j];
values[j + ] = values[j];
j--;
}
arr[j + ] = key;
values[j + ] = init;
}
}
static int SelectPivotMedianOfThree(double[] values, List<int> arr, int low, int high)
{
int mid = low + ((high - low) >> );//计算数组中间的元素的下标 //使用三数取中法选择枢轴
if (values[mid] > values[high])//目标: arr[mid] <= arr[high]
{
swap(values, arr, mid, high);
}
if (values[low] > values[high])//目标: arr[low] <= arr[high]
{
swap(values, arr, low, high);
}
if (values[mid] > values[low]) //目标: arr[low] >= arr[mid]
{
swap(values, arr, mid, low);
}
//此时，arr[mid] <= arr[low] <= arr[high]
return low;
//low的位置上保存这三个位置中间的值
//分割时可以直接使用low位置的元素作为枢轴，而不用改变分割函数了
}
static void swap(double[] values, List<int> arr, int t1, int t2)
{
double temp = values[t1];
values[t1] = values[t2];
values[t2] = temp;
int key = arr[t1];
arr[t1] = arr[t2];
arr[t2] = key;
}
static void QSort(double[] values, List<int> arr, int low, int high)
{
int first = low;
int last = high; int left = low;
int right = high; int leftLen = ;
int rightLen = ; if (high - low + < )
{
InsertSort(values, arr, low, high);
return;
} //一次分割
int key = SelectPivotMedianOfThree(values, arr, low, high);//使用三数取中法选择枢轴
double inti = values[key];
int currentKey = arr[key]; while (low < high)
{
while (high > low && values[high] >= inti)
{
if (values[high] == inti)//处理相等元素
{
swap(values, arr, right, high);
right--;
rightLen++;
}
high--;
}
arr[low] = arr[high];
values[low] = values[high];
while (high > low && values[low] <= inti)
{
if (values[low] == inti)
{
swap(values, arr, left, low);
left++;
leftLen++;
}
low++;
}
arr[high] = arr[low];
values[high] = values[low];
}
arr[low] = currentKey;
values[low] = values[key];
//一次快排结束
//把与枢轴key相同的元素移到枢轴最终位置周围
int i = low - ;
int j = first;
while (j < left && values[i] != inti)
{
swap(values, arr, i, j);
i--;
j++;
}
i = low + ;
j = last;
while (j > right && values[i] != inti)
{
swap(values, arr, i, j);
i++;
j--;
}
QSort(values, arr, first, low - - leftLen);
QSort(values, arr, low + + rightLen, last);
}
#endregion
/// <summary>
/// 寻找最佳的分裂点
/// </summary>
/// <param name="num"></param>
/// <param name="node"></param>
public static Node findBestSplit(Node node,List<int> nums,int[] isUsed)
{
try
{
//判断是否继续分裂
double totalShang = getGini(node.ClassCount, node.rowCount);
if (ifEnd(node, totalShang, isUsed))
{
return node;
}
#region 变量声明
SplitInfo info = new SplitInfo();
info.initial();
int RowCount = nums.Count; //样本总数
double jubuMax = ; //局部最大熵
int splitPoint = ; //分裂的点
double splitValue = ; //分裂的值
#endregion
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
continue;
}
#region 离散变量
if (type[i] == )
{
double[][] allCount = new double[allNum[i]][];
for (int j = ; j < allCount.Length; j++)
{
allCount[j] = new double[classCount];
}
int[] countAllFeature = new int[allNum[i]];
List<int>[] temp = new List<int>[allNum[i]];
double[] allClassCount = node.ClassCount; //所有类别的数量
for (int j = ; j < temp.Length; j++)
{
temp[j] = new List<int>();
}
for (int j = ; j < nums.Count; j++)
{
int index = Convert.ToInt32(allData[nums[j]][i]);
temp[index - ].Add(nums[j]);
countAllFeature[index - ]++;
allCount[index - ][Convert.ToInt32(allData[nums[j]][lieshu - ]) - ]++;
}
double allShang = ;
int choose = ; double[][] jubuCount = new double[][];
for (int k = ; k < allCount.Length; k++)
{
if (temp[k].Count == )
continue;
double JubuShang = ;
double[][] tempCount = new double[][];
tempCount[] = allCount[k];
tempCount[] = new double[allCount[].Length];
for (int j = ; j < tempCount[].Length; j++)
{
tempCount[][j] = allClassCount[j] - allCount[k][j];
}
JubuShang = JubuShang + getGini(tempCount[], countAllFeature[k]) * countAllFeature[k] / RowCount;
int nodecount = RowCount - countAllFeature[k];
JubuShang = JubuShang + getGini(tempCount[], nodecount) * nodecount / RowCount;
if (JubuShang < allShang)
{
allShang = JubuShang;
jubuCount = tempCount;
choose = k;
}
}
if (allShang < jubuMax)
{
info.type = ;
jubuMax = allShang;
info.class_Count = jubuCount;
info.temp[] = temp[choose];
info.temp[] = new List<int>();
info.features = new List<string>();
info.features.Add((choose + ) + "");
info.features.Add("");
for (int j = ; j < temp.Length; j++)
{
if (j == choose)
continue;
for (int k = ; k < temp[j].Count; k++)
{
info.temp[].Add(temp[j][k]);
}
if (temp[j].Count != )
{
info.features[] = info.features[] + (j + ) + ",";
}
}
info.splitIndex = i;
}
}
#endregion
#region 连续变量
else
{
double[] leftCunt = new double[classCount]; //做节点各个类别的数量
double[] rightCount = new double[classCount]; //右节点各个类别的数量
double[] count1 = new double[classCount]; //子集1的统计量
double[] count2 = new double [node.ClassCount.Length]; //子集2的统计量
for (int j = ; j < node.ClassCount.Length; j++)
{
count2[j] = node.ClassCount[j];
}
int all1 = ; //子集1的样本量
int all2 = nums.Count; //子集2的样本量
double lastValue = ; //上一个记录的类别
double currentValue = ; //当前类别
double lastPoint = ; //上一个点的值
double currentPoint = ; //当前点的值
double[] values = new double[nums.Count];
for (int j = ; j < values.Length; j++)
{
values[j] = allData[nums[j]][i];
}
QSort(values, nums, , nums.Count - );
double lianxuMax = ; //连续型属性的最大熵
#region 寻找最佳的分割点
for (int j = ; j < nums.Count - ; j++)
{
currentValue = allData[nums[j]][lieshu - ];
currentPoint = (allData[nums[j]][i]);
if (j == )
{
lastValue = currentValue;
lastPoint = currentPoint;
}
if (currentValue != lastValue && currentPoint != lastPoint)
{
double shang1 = getGini(count1, all1);
double shang2 = getGini(count2, all2);
double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2);
//allShang = (totalShang - allShang);
if (lianxuMax > allShang)
{
lianxuMax = allShang;
for (int k = ; k < count1.Length; k++)
{
leftCunt[k] = count1[k];
rightCount[k] = count2[k];
}
splitPoint = j;
splitValue = (currentPoint + lastPoint) / ;
}
}
all1++;
count1[Convert.ToInt32(currentValue) - ]++;
count2[Convert.ToInt32(currentValue) - ]--;
all2--;
lastValue = currentValue;
lastPoint = currentPoint;
}
#endregion
#region 如果超过了局部值，重设
if (lianxuMax < jubuMax)
{
info.type = ;
info.splitIndex = i;
info.features=new List<string>() {splitValue+""};
//finalPoint = splitPoint;
jubuMax = lianxuMax;
info.temp[] = new List<int>();
info.temp[] = new List<int>();
for (int k = ; k < splitPoint; k++)
{
info.temp[].Add(nums[k]);
}
for (int k = splitPoint; k < nums.Count; k++)
{
info.temp[].Add(nums[k]);
}
info.class_Count[] = new double [leftCunt.Length];
info.class_Count[] = new double [leftCunt.Length];
for (int k = ; k < leftCunt.Length; k++)
{
info.class_Count[][k] = leftCunt[k];
info.class_Count[][k] = rightCount [k];
}
}
#endregion
}
#endregion
}
#region 没有寻找到最佳的分裂点，则设置为叶节点
if (info.splitIndex == -)
{
double[] finalCount = node.ClassCount;
double max = finalCount[];
int result = ;
for (int i = ; i < finalCount.Length; i++)
{
if (finalCount[i] > max)
{
max = finalCount[i];
result = (i + );
}
}
node.feature_Type="result";
node.features=new List<String> { "" + result };
return node;
}
#endregion
#region 分裂
int deep = node.deep;
node.SplitFeature = ("" + info.splitIndex);
List<Node> childNode = new List<Node>();
int[][] used = new int[][];
used[] = new int[isUsed.Length];
used[] = new int[isUsed.Length];
for (int i = ; i < isUsed.Length; i++)
{
used[][i] = isUsed[i];
used[][i] = isUsed[i];
}
if (info.type == )
{
used[][info.splitIndex] = ;
node.feature_Type = ("离散");
}
else
{
//used[info.splitIndex] = 0;
node.feature_Type = ("连续");
}
List<int>[] rowIndex = info.temp;
List<String> features = info.features;
Node node1 = new Node();
Node node2 = new Node();
node1.setClassCount(info.class_Count[]);
node2.setClassCount(info.class_Count[]);
node1.rowCount = info.temp[].Count;
node2.rowCount = info.temp[].Count;
node1.deep = deep + ;
node2.deep = deep + ;
node1 = findBestSplit(node1, info.temp[],used[]);
node2 = findBestSplit(node2, info.temp[], used[]);
node.leafNode_Count = (node1.leafNode_Count +node2.leafNode_Count);
node.leafWrong = (node1.leafWrong+node2.leafWrong);
node.features = (features);
childNode.Add(node1);
childNode.Add(node2);
node.childNodes = childNode;
#endregion
return node;
}
catch (Exception e)
{
Console.WriteLine(e.StackTrace);
return node;
}
}
/// <summary>
/// GINI值
/// </summary>
/// <param name="counts"></param>
/// <param name="countAll"></param>
/// <returns></returns>
public static double getGini(double[] counts, int countAll)
{
double Gini = ;
for (int i = ; i < counts.Length; i++)
{
Gini = Gini - Math.Pow(counts[i] / countAll, );
}
return Gini;
}
#region CCP剪枝
public static void getSeries(Node node)
{
Stack<Node> nodeStack = new Stack<Node>();
if (node != null)
{
nodeStack.Push(node);
}
if (node.feature_Type == "result")
return;
List<Node> childs = node.childNodes;
for (int i = ; i < childs.Count; i++)
{
getSeries(node);
}
}
/// <summary>
/// 遍历剪枝
/// </summary>
/// <param name="node"></param>
public static Node getNode1(Node node, Node nodeCut)
{ //List<Node> childNodes = node.getChild();
//double min = 100000;
////Node nodeCut = new Node();
//double temp = 0;
//for (int i = 0; i < childNodes.Count; i++)
//{
// if (childNodes[i].getType() != "result")
// {
// //if (!cutTree(childNodes[i]))
// temp = min;
// min = cutTree(childNodes[i], min);
// if (min < temp)
// nodeCut = childNodes[i];
// getNode1(childNodes[i], nodeCut);
// }
//}
//node.setChildNode(childNodes);
return null;
}
/// <summary>
/// 对每一个节点剪枝
/// </summary>
public static double cutTree(Node node, double minA)
{
int rowCount = node.rowCount;
double leaf = node.getErrorCount();
double[] values = getError1(node, , );
double treeWrong = values[];
double son = values[];
double rate = (leaf - treeWrong) / (son - );
if (minA > rate)
minA = rate;
//double var = Math.Sqrt(treeWrong * (1 - treeWrong / rowCount));
//double panbie = treeWrong + var - leaf;
//if (panbie > 0)
//{
// node.setFeatureType("result");
// node.setChildNode(null);
// int result = (node.getResult() + 1);
// node.setFeatures(new List<String>() { "" + result });
// //return true;
//}
return minA;
}
/// <summary>
/// 获得子树的错误个数
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
public static double[] getError1(Node node, double treeError, double son)
{
if (node.feature_Type == "result")
{ double error = node.getErrorCount();
son++;
return new double[] { treeError + error, son };
}
List<Node> childNode = node.childNodes;
for (int i = ; i < childNode.Count; i++)
{
double[] values = getError1(childNode[i], treeError, son);
treeError = values[];
son = values[];
}
return new double[] { treeError, son };
}
#endregion
CART核心代码
总结：
（1）CART是一棵二叉树，每一次分裂会产生两个子节点，对于连续性的数据，直接采用与C4.5相似的处理方法，对于离散型数据，选择最优的两种离散值组合方法。
（2）CART既能是分类数，又能是二叉树。如果是分类树，将选择能够最小化分裂后节点GINI值的分裂属性；如果是回归树，选择能够最小化两个节点样本方差的分裂属性。
（3）CART跟C4.5一样，需要进行剪枝，采用CCP（代价复杂度的剪枝方法）。
决策树系列（五）——CART的更多相关文章
- 大白话5分钟带你走进人工智能-第二十六节决策树系列之Cart回归树及其参数(5)
第二十六节决策树系列之Cart回归树及其参数(5) 上一节我们讲了不同的决策树对应的计算纯度的计算方法, ...
- CSS 魔法系列：纯 CSS 绘制各种图形《系列五》
我们的网页因为 CSS 而呈现千变万化的风格.这一看似简单的样式语言在使用中非常灵活,只要你发挥创意就能实现很多比人想象不到的效果.特别是随着 CSS3 的广泛使用,更多新奇的 CSS 作品涌现出来. ...
- Netty4.x中文教程系列(五)编解码器Codec
Netty4.x中文教程系列(五)编解码器Codec 上一篇文章详细解释了ChannelHandler的相关构架设计,版本和设计逻辑变更等等. 这篇文章主要在于讲述Handler里面的Codec,也就 ...
- WCF编程系列(五)元数据
WCF编程系列(五)元数据 示例一中我们使用了scvutil命令自动生成了服务的客户端代理类: svcutil http://localhost:8000/?wsdl /o:FirstServic ...
- JVM系列五:JVM监测&工具
JVM系列五:JVM监测&工具[整理中] http://www.cnblogs.com/redcreen/archive/2011/05/09/2040977.html 前几篇篇文章介绍了介 ...
- SQL Server 2008空间数据应用系列五：数据表中使用空间数据类型
原文:SQL Server 2008空间数据应用系列五:数据表中使用空间数据类型 友情提示,您阅读本篇博文的先决条件如下: 1.本文示例基于Microsoft SQL Server 2008 R2调测 ...
- VSTO之旅系列(五)：创建Outlook解决方案
原文:VSTO之旅系列(五):创建Outlook解决方案 本专题概要 引言 Outlook对象模型 自定义Outlook窗体 小结 一.引言 在上一个专题中,为大家简单介绍了下如何创建Word解决方案 ...
- 系列五AnkhSvn
原文:系列五AnkhSvn AnkhSvn介绍 AnkhSVN是一款在VS中管理Subversion的插件,您可以在VS中轻松的提交.更新.添加文件,而不用在命令行或资源管理器中提交.而且该插件属于开 ...
- java多线程系列(五)---synchronized ReentrantLock volatile Atomic 原理分析
java多线程系列(五)---synchronized ReentrantLock volatile Atomic 原理分析 前言:如有不正确的地方,还望指正. 目录 认识cpu.核心与线程 java ...
随机推荐
- BZOJ 3309: DZY Loves Math [莫比乌斯反演 线性筛]
题意:\(f(n)\)为n的质因子分解中的最大幂指数,求\(\sum_{i=1}^n \sum_{j=1}^m f(gcd(i,j))\) 套路推♂倒 \[ \sum_{D=1}^n \sum_{d| ...
- 升级gitlab
https://gitlab.com/gitlab-org/gitlab-ce/tree/master/doc/update https://about.gitlab.com/update/#cent ...
- Linux系统Go开发环境搭建
Go 语言是由谷歌的科学家开发的,并开源的新语言,被誉为"21世纪的C语言",它的主要目标是将静态语言的安全性和高效性与动态语言的易开发性进行有机结合,达到完美平衡,从而使编程变得 ...
- [记]Debian alias 设置, 不设置貌似有点不方便习惯
备忘录,记录下. 不知道 当前有那些 alias 的话 直接输入 alias ,回车就可以看到 alias 列表. 终端输入: vim ~/bash_aliases 然后输入: # some more ...
- PHP实现WebService的简单示例和实现步骤
首先我创建的文件有: api.php api的接口类文件 api.wsdl 我创建产生的最后要调用的接口文件 cometrue.php 注册service api类内容的所有内容的执行文件 creat ...
- 正本清源区块链——Caoz
正本清源区块链 说明:以下内容整理自Caoz的<正本清源区块链>,如有不妥,请联系我修改或删除. 简介 不讨论炒币!不讨论炒币!不讨论炒币! 本课程内容分为两部分: 第一部分,烧脑篇,介绍 ...
- 枚举enum学习小记
参考文献: [1]C++程序设计语言(特别版), 裘宗燕译, 机械工业出版社 [2]C++ Primer (3rd Ed.), S.B. Lippman and J. Lajoie, 人民邮电出版社 ...
- 有了Openvswitch和Docker，终于可以做《TCP/IP详解》的实验了！
所有做过网络编程的程序员,想必都会看<TCP/IP详解>卷一:协议 后来出了第二版,但是由于第一版才是Rechard Stevens的原版,本人还是多次看了第一版. 对这一版印象最深的就是 ...
- 《精通android网络开发》--HTTP数据通信
No1: 例如:http://www.*****.com/china/index.htm 1)http:// 代表超文本传送协议,通知*****.com服务器显示web页,通常不用输入 2)www 代 ...
- dfs练习
不给提示,练习. 题意: 蒜头的数学实在是太差了,于是老师把他关到小黑屋让他闭门修炼.老师跟他一张纸,上面一排写着1, 2, 3...N这N个数,中间用空白分隔.老师让他在空白处填上加号或者减号.他让 ...