【Bzoj 1835 基站选址】

基站选址的区间里隐藏着DP优化的机密……

分析：

      不论是做过乘积最大还是石子合并，或者是其他的入门级别的区间DP题目的人呐，大米并认为读题后就能够轻松得出一个简洁明了的Dp转移方程。

      由于这道题每个村庄i仅有两种状态：①自己有一个基站②自己不是基站，但是自己的范围S[i]里有基站。基于这样的关系，可以得出一个容易理解的Dp转移方程：

      [设f[k][i]表示1~i的村庄中选取k个村庄安放基站，并且第k个村庄就安放在村庄i，使得所有村庄合法的最小花费]

        f[k][i]=min(f[k-1][j]+Cost(j,i))+c[i] (j<i)

     这个状态转移表达的含义是，村庄i,j安放了基站。据此Cost(i,j)表示的则是在村庄i,j之间没能接收到基站信号的基站的额外费用w[i]之和(即表示由于不能用基站处理掉而付出的额外代价)。

      到此为止这个解法已经成功了一半。不成功的地方是时间复杂度在本提数据范围下是不能承受的——O(n²k)。

      因此我们考虑Dp的优化。让我们幻想一下，如果能够存下f[k-1][]+Cost们的最优值，那么就不需要对于每个i转移花n次来枚举来源了！随后可以发现，难点在于Cost(i,j)的快速计算。

      仔细分析Cost(i,j)的定义，我们需要找到一种方法，能够快速求出在两个基站i,j之间有哪些村庄无法被覆盖(调皮的是,这里覆盖范围是按各个村庄来定的)。由于f[k][i]表示合法方案，所以在状态转移的时候，我们要注意对于[1,j]之间的村庄已经处理好，我们只要考虑(j,i)中村庄是否覆盖的问题。那么如果一个村庄无法被j,i两个村庄覆盖，它的信号接收范围长啥样呢？

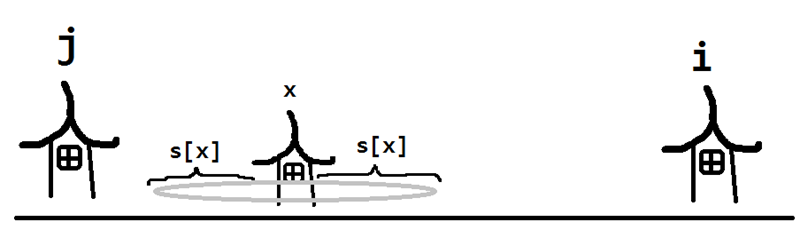
     就是这样：左手摸不着j,右手碰不到i。然后我们尝试利用范围这一特性，我们发现，如果(j,i)这一对组合,x覆盖不到，那么对于所有(j,I)（I大于i）都覆盖不到x。所以我们想到，一种(j,i)可以为后来的(j,I)提供一些小小信息。同理地，如果(j,i)这一对组合,x覆盖不到,那么对于所有(J,i)（J小于j）都覆盖不到x。总结来说啦，就是一种单调性：

     结论：如果状态转移中(j,i)情况下(表示在i,j放置基站),如果之间某个村庄x无法被覆盖，那么对于所有状态转移中(J,I)[J<j&&I>i]都无法覆盖x(毕竟越来越远了嘛)。

     为了方便，我们动用三个数组参与Dp的优化行动：

     ·int left_cur[i]：表示在村庄i的范围内[-s[i],+s[i]],最靠左边的那个村庄的位置(也就是下标最小的点，放置基站依旧可以覆盖i);

     ·int left_cur[i]：表示在村庄i的范围内[-s[i],+s[i]],最靠右边的那个村庄的位置(也就是下标最大的点，放置基站依旧可以覆盖i);

     ·vector<int> cur_right[i]：用于存储所有right_cur的值都为i村庄的点的下标(和前一个玩意儿互逆似的)。

     当前状态转移f[k][i]=min(f[k-1][j]+Cost(i,j))+c[i]完成后，我们将以i为 right_cur的值的点全部枚举一遍(使用数组cur_right)，对于每个枚举的点再依靠left_cur[i]找到最左边能够覆盖该点的村庄下标p。这样做是干啥呢？因为i即将循环至i+1那么下面的状态对于所有(P,I)[P<p,I>i]都不可能覆盖这些枚举的点了，那么这些点的w(额外费用)必然会贡献Cost所以我们先给这些点(即1~p-1的点)加上这个Cost，然后维护这些f[k-1][]+Cost的最小值用于下一次转移就可以了——用啥维护可以支持区间加和区间求最值？线段树！

      代码长出来了：

 #include<vector>
 #include<stdio.h>
 #include<algorithm>
 #define ll long long
 #define inf 1ll*100000000*100000000
 #define In(a,p) go(i,p,n)scanf("%d",a+i)
 #define go(i,a,b) for(int i=a;i<=b;i++)
 #define ro(i,a,b) for(int i=a;i>=b;i--)
 using namespace std;
 const int N=;int n,K;
 ll d[N],c[N],s[N],w[N],f[N],left_cur[N],ans=inf,W;
 vector<int>cur_right[N];
 struct Binary_Search
 {
     int l,r,M,res;
     int Left_Search(int i){l=,r=res=i;
         while(l<=r)d[i]-d[M=l+r>>]<=s[i]?res=M,r=M-:l=M+;return res;}
     int Right_Search(int i){l=res=i,r=n;
         while(l<=r)d[M=l+r>>]-d[i]<=s[i]?res=M,l=M+:r=M-;return res;}
 }dichotomy;
 struct Segment_Tree
 {
     int sz,lch[N*],rch[N*];ll lazy[N*],Min[N*];
     void Init(){sz=;int _;Build(_,,n);}
     void Push_Up(int u){Min[u]=min(Min[lch[u]],Min[rch[u]]);}
     void Push_Down(int u)
     {
         lazy[lch[u]]+=lazy[u];lazy[rch[u]]+=lazy[u];
         Min[lch[u]]+=lazy[u];Min[rch[u]]+=lazy[u];lazy[u]=;
     }
     void Build(int &u,int l,int r)
     {
         lazy[u=++sz]=;if(l==r){Min[u]=f[l];return;}
         int M=l+r>>;Build(lch[u],l,M);Build(rch[u],M+,r);Push_Up(u);
     }
     void Update(int u,int l,int r,int L,int R,ll d)
     {
         if(L>R)return;Push_Down(u);
         if(l==L&&r==R){Min[u]+=d;lazy[u]+=d;return;}
         int M=l+r>>;if(R<=M)Update(lch[u],l,M,L,R,d);
         else if(L>M)Update(rch[u],M+,r,L,R,d);
         else Update(lch[u],l,M,L,M,d),Update(rch[u],M+,r,M+,R,d);Push_Up(u);
     }
     ll Query(int u,int l,int r,int L,int R)
     {
         if(L>R)return ;Push_Down(u);
         if(l==L&&r==R){return Min[u];}
         int M=l+r>>;if(R<=M)return Query(lch[u],l,M,L,R);
         else if(L>M)return Query(rch[u],M+,r,L,R);
         else return min(Query(lch[u],l,M,L,M),Query(rch[u],M+,r,M+,R));Push_Up(u);
     }
 }maintain;
 int main()
 {
     scanf("%d%d",&n,&K);In(d,);In(c,);In(s,);In(w,);

     go(i,,n)
     {
         left_cur[i]=dichotomy.Left_Search(i);
         int right=dichotomy.Right_Search(i);
         cur_right[right].push_back(i);
     }
     n++;K++;w[n]=d[n]=inf;

     go(i,,n){f[i]=c[i];go(j,,i-)if(d[j]+s[j]<d[i])f[i]+=w[j];}ans=f[n];
     go(k,,K)
     {
         maintain.Init();go(i,,n)
         {
             f[i]=maintain.Query(,,n,,i-)+c[i];
             if(cur_right[i].size())go(j,,cur_right[i].size()-)
             {
                 int Pos=cur_right[i][j];
                 maintain.Update(,,n,,left_cur[Pos]-,w[Pos]);
             }
         }
         ans=min(ans,f[n]);
     }
     printf("%lld\n",ans);return ;
 }//Paul_Guderian

有人说大米饼喜欢压代码，这里有一份不压的————我也会写不压的！

 #include<vector>
 #include<stdio.h>
 #include<algorithm>
 #define ll long long
 #define inf 1ll*100000000*100000000
 #define In(a,p) go(i,p,n)scanf("%d",a+i)
 #define go(i,a,b) for(int i=a;i<=b;i++)
 #define ro(i,a,b) for(int i=a;i>=b;i--)
 using namespace std;
 const int N=;int n,K;
 ll d[N],c[N],s[N],w[N],f[N],left_cur[N],ans=inf,W;
 vector<int>cur_right[N];
 struct Binary_Search
 {
     int l,r,mid;
     int Left_Search(int i)
     {
         l=,r=i;int res=i;
         while(l<=r)
         {
             mid=l+r>>;
             if(d[i]-d[mid]<=s[i])res=mid,r=mid-;
             else l=mid+;
         }
         return res;
     }
     int Right_Search(int i)
     {
         l=i,r=n;int res=i;
         while(l<=r)
         {
             mid=l+r>>;
             if(d[mid]-d[i]<=s[i])res=mid,l=mid+;
             else r=mid-;
         }
         return res;
     }
 }dichotomy;
 struct Segment_Tree
 {
     int sz,lch[N*],rch[N*];ll lazy[N*],Min[N*];
     void Init(){sz=;int _;Build(_,,n);}
     void Push_Up(int u)
     {
         Min[u]=min(Min[lch[u]],Min[rch[u]]);
     }
     void Push_Down(int u)
     {
         lazy[lch[u]]+=lazy[u];
         lazy[rch[u]]+=lazy[u];
         Min[lch[u]]+=lazy[u];
         Min[rch[u]]+=lazy[u];
         lazy[u]=;
     }
     void Build(int &u,int l,int r)
     {
         lazy[u=++sz]=;
         if(l==r)
         {
             Min[u]=f[l];
             return;
         }
         int M=l+r>>;
         Build(lch[u],l,M);
         Build(rch[u],M+,r);
         Push_Up(u);
     }
     void Update(int u,int l,int r,int L,int R,ll d)
     {
         if(L>R)return;
         Push_Down(u);
         if(l==L&&r==R)
         {
             Min[u]+=d;
             lazy[u]+=d;
             return;
         }
         int M=l+r>>;
         if(R<=M)Update(lch[u],l,M,L,R,d);
         else if(L>M)Update(rch[u],M+,r,L,R,d);
         else Update(lch[u],l,M,L,M,d),Update(rch[u],M+,r,M+,R,d);
         Push_Up(u);
     }
     ll Query(int u,int l,int r,int L,int R)
     {
         if(L>R)return ;
         Push_Down(u);
         if(l==L&&r==R)
         {
             return Min[u];
         }
         int M=l+r>>;
         if(R<=M)return Query(lch[u],l,M,L,R);
         else if(L>M)return Query(rch[u],M+,r,L,R);
         else return min(Query(lch[u],l,M,L,M),Query(rch[u],M+,r,M+,R));
         Push_Up(u);
     }
 }maintain;
 void Input_Data()
 {
     scanf("%d%d",&n,&K);
     In(d,);In(c,);In(s,);In(w,);
 }
 void Add_Ans_Point()
 {
     n++;K++;
     w[n]=d[n]=inf;
 }
 void Pre_Handle_of_Dynamic_Programming()
 {
     go(i,,n)
     {
         left_cur[i]=dichotomy.Left_Search(i);
         int right=dichotomy.Right_Search(i);
         cur_right[right].push_back(i);
     }
     Add_Ans_Point();
 }
 void Init_First_Status()
 {
     go(i,,n)
     {
         f[i]=c[i];
         go(j,,i-)
         {
             if(d[j]+s[j]<d[i])
             {
                 f[i]+=w[j];
             }
         }
     }
 }
 void Optimized_Dynamic_Programming()
 {
     Init_First_Status();
     ans=f[n];
     go(k,,K)
     {
         maintain.Init();
         go(i,,n)
         {
             f[i]=maintain.Query(,,n,,i-)+c[i];
             if(cur_right[i].size())
             {
                 go(j,,cur_right[i].size()-)
                 {
                     int Pos=cur_right[i][j];
                     maintain.Update(,,n,,left_cur[Pos]-,w[Pos]);
                 }
             }
         }
         ans=min(ans,f[n]);
     }
     printf("%lld\n",ans);
 }
 int main()
 {
     freopen("in.in","r",stdin);

     Input_Data();

     Pre_Handle_of_Dynamic_Programming();

     Optimized_Dynamic_Programming();

     return ;
 }//Paul_Guderian

【条理清晰？】

     

我无法忘记那只廉价的吉他

和那件破旧的蓝色军装。————汪峰《雨天的回忆》