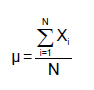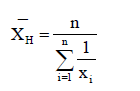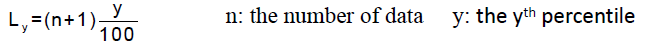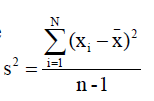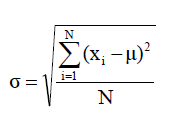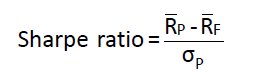QM3_Statistics Concepts and Market Returns

Basic Concepts

Terms

Descriptive Statistics

• Describes the important aspects of large data sets.
  • 统计
  • 概率
  • 分布

Inferential statistics

• Involves making forecasts, estimates, or judgments about a larger group from the smaller group.
  • 预测
  • 估计
  • 判断

Measurement scales

考点:

• 给描述, 判断是哪种尺度
• 给尺度, 判断孰强孰弱

Frequency distribution

Central Tendency (第一维度,中心趋势)

Mean

Calculation

• Arithmetic mean (算术平均)
  • Population Mean
    • 
  • Sample Mean
    • 
• Geometric mean (几何平均)
  • 

• Harmonic mean (调和平均, I级考试不考)
  • 

• Weighted mean (加权平均)
  • 
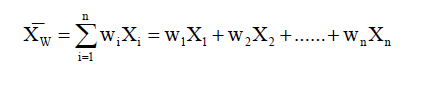
  • 样本均值中相当于权重都是1/n, 而weighted mean就是不等权重(w1,w2,...wn).

Properties (性质)

• Arithmetic mean : 单期收益率的表现
  • focus on average single-period performance
  • sensitive to extreme values

• Geometric mean: 多期收益率的表现
  • focus on multi-period performance
• Weighted mean: 多用于计算期望值 (算期望就是算加权平均)
  • userd to calculate the portfolio return/expected value based on probabilities
• Harmonic Mean <= Geometric Mean <= Arithmetic Mean

• Median 中位数 与 Mode 众数
  • 例: 一组数, 1,1,2,4,8.
  • median: 一共有五个数, 中间的数是2, 所以median是2. 若这个数组是1,2,4,8. 中位数则是(2+4)/2 = 3.
  • mode : 1出现了两次, 所以众数是1.

Quantile (分位点) **

Definition

• A value at or below which a stated fraction of the data lies.
  • Quantiles 四分位点
  • Quintiles 五分位点
  • Deciles 十分位点
  • Percentiles 百分位点
  • 

Calculation

• Step 1: formula for location of data in ascending order (必须先把所有数据从小到大排列)
• Step 2: 用公式计算
  • 

• 例: for data with 17 observations, find out the location of 3rd quintile.
  • 
  • 注:      1. value 中10和11的顺序写错了, 数值应该是要按顺序排列的.
    • 2. 如果要计算3rd quintile这个位置上的值的话, 应该是(20+23)/2.　　　　

考点

• 描述
  • 例: 第一个四分位点 --> 有25%的数小于第一个四分位点(因数据是ascending order排列的,所以是小于).
• 计算
  • Ly = (n+1)y/100 (算location)
  • 算value (算特定分位点的数值)

金融有风险, 风险有不确定性, 所以用离散程度来度量风险, 方差或者标准差就是用来度量离散程度的;

金融中的收益用均值 mean 来度量.

Risk <-- uncertainty <-- dispersion <-- variance, standard deviation

Dispersion (第二维度,离散程度,即偏离均值的程度)

Absolute dispersion (绝对离散程度)

Range (范围)

• Maximum Value - Minimum Value

Mean Absolute Deviation (MAD, 均值绝对偏差)

• MAD <= 西格玛
• 

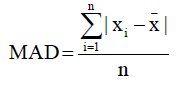
Variance (方差)

• MAD是绝对值, 不好计算,所以平方之后就引入了方差.
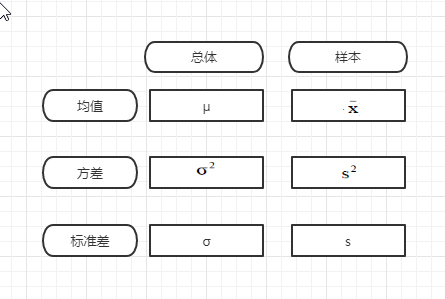
• Population 总体
  • 

• Sample 样本
  • 

Standard deviation (标准差, 把方差开根号)

• Population 总体
  • 

• Sample 样本
  • 
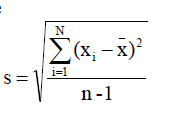
  • n-1 是为了满足无偏性或者自由度

Relative dispersion (相对离散程度) ***

Coefficient of variation (CV, 变异系数)

• 每赚一块钱所承担的风险
• Calculation
  • 
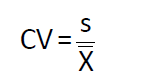
  • s: 样本标准差 (代表风险); x拔: 样本均值(代表收益)

• Characteristics
  • CV has no units of measurement
  • a measure of risk per unit of mean return
  • the lower the better

Sharpe ratio (夏普比率)

• 每承担单位风险所获得的超额收益率
• Calculation
  • 

• Characteristics
  • Sharpe ratio has no units of measurement
  • a measure of exccess return per unit of risk
  • the higher the better

考点

• 计算

  • CV
  • Sharpe ratio

• 描述

  • CV: 每赚一块钱所承担的风险
  • Sharpe ratio: 每承担单位风险所获得的超额收益
• 性质
  • 变异系数CV越小越好
  • Sharpe ratio越大越好

Chebyshev's inequality (切比雪夫不等式)

• 概念
  • For any distribution with finite variance, the minimum percentage of observations that lie within k standard deviation of the mean would be 1-1/k*k, given k>1.
  • 对任何一组观测值, 个休落在均值周围k个标准差之内的概率不小于1-1/k*k, 对任意k>1.
• 例题
  • 

考点

• 已知k, 需要计算概率1-1/k*k
• 已知概率, 需要反算出k, 再算出区间
• 已知区间, 需要计算k, 再算出概率

Skewness (第三维度,偏度) ***

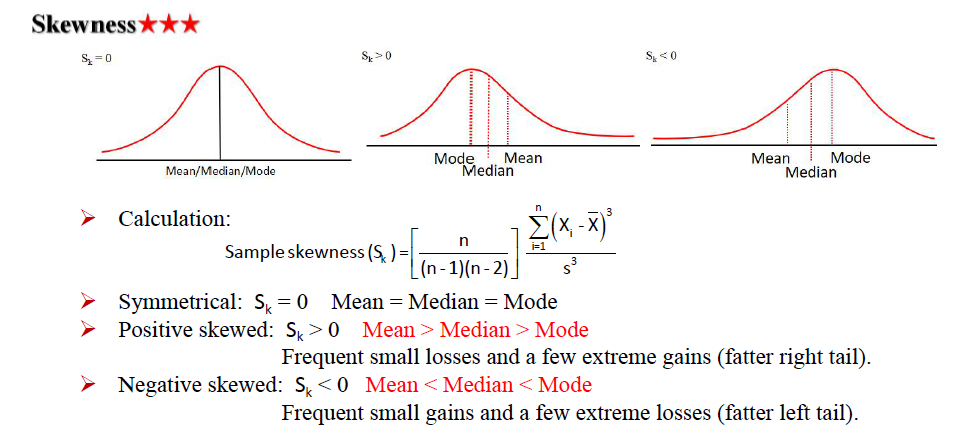
肥尾: 取到极端值的概率较大

Kurtosis (第四维度,峰度) **

正态分布的峰度定义为3.

T-分布有特殊, 是低峰肥尾. ? 哪一章提到?

Z-分布?