MCMC算法解析

MCMC算法的核心思想是我们已知一个概率密度函数，需要从这个概率分布中采样，来分析这个分布的一些统计特性，然而这个这个函数非常之复杂，怎么去采样？这时，就可以借助MCMC的思想。

它与变分自编码不同在于：VAE是已知一些样本点，这些样本肯定是来自于同一分布，但是我们不知道这个分布函数的具体表达式，然而我们需要从这个分布中去采取新的样本，怎么采样，这时，就需要借助VAE的思想。

个人的一点总结，不知道是否正确，如果有不同的理解，希望指正批评！

MCMC原理讲解

以下内容博客转自：https://www.cnblogs.com/xbinworld/p/4266146.html

背景

随机模拟也可以叫做蒙特卡罗模拟(Monte Carlo Simulation)。这个方法的发展始于20世纪40年代，和原子弹制造的曼哈顿计划密切相关，当时的几个大牛，包括乌拉姆、冯.诺依曼、费米、费曼、Nicholas Metropolis， 在美国洛斯阿拉莫斯国家实验室研究裂变物质的中子连锁反应的时候，开始使用统计模拟的方法,并在最早的计算机上进行编程实现。[3]

随机模拟中有一个重要的问题就是给定一个概率分布p(x)，我们如何在计算机中生成它的样本。一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的。 通过线性同余发生器可以生成伪随机数，我们用确定性算法生成[0,1]之间的伪随机数序列后，这些序列的各种统计指标和均匀分布 Uniform(0,1) 的理论计算结果非常接近。这样的伪随机序列就有比较好的统计性质，可以被当成真实的随机数使用。

下面总结这么几点：

1、蒙特卡洛数值积分

2、均匀分布，Box-Muller 变换

3、Monte Carlo principle

4、接受-拒绝抽样（Acceptance-Rejection sampling)

5、重要性抽样(Importance sampling)

6、马尔科夫链，马尔科夫稳态

7、MCMC——Metropolis-Hasting算法

8、MCMC——Gibbs Sampling算法

1、蒙特卡洛数值积分

如果我们要求f(x)的积分，如

而f(x)的形式比较复杂积分不好求，则可以通过数值解法来求近似的结果。常用的方法是蒙特卡洛积分：

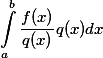
这样把q(x)看做是x在区间内的概率分布，而把前面的分数部门看做一个函数，然后在q(x)下抽取n个样本，当n足够大时，可以用采用均值来近似：

因此只要q（x）比较容易采到数据样本就行了。随机模拟方法的核心就是如何对一个概率分布得到样本，即抽样（sampling）。下面我们将介绍常用的抽样方法。

2、均匀分布，Box-Muller 变换

在计算机中生成[0,1]之间的伪随机数序列，就可以看成是一种均匀分布。而随机数生成方法有很多，最简单的如：

当然计算机产生的随机数都是伪随机数，不过一般也就够用了。

[Box-Muller 变换]  如果随机变量 U1,U2 独立且U1,U2∼Uniform[0,1]，

则 Z0,Z1 独立且服从标准正态分布。

3、Monte Carlo principle

Monte Carlo 抽样计算随即变量的期望值是接下来内容的重点：X 表示随即变量，服从概率分布 p(x), 那么要计算 f(x) 的期望，只需要我们不停从 p(x) 中抽样xi，然后对这些f（xi）取平均即可近似f(x)的期望。

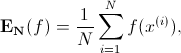
4、接受-拒绝抽样（Acceptance-Rejection sampling)[2]

很多实际问题中，p(x)是很难直接采样的的，因此，我们需要求助其他的手段来采样。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的，其中q(x)叫做 proposal distribution 。

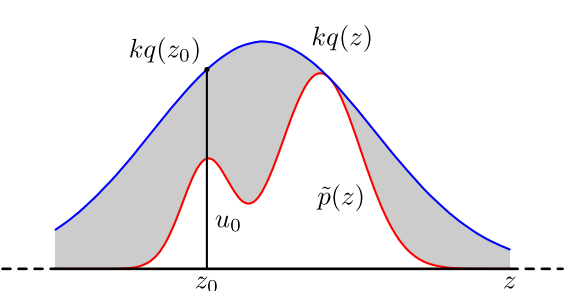
具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。（参考上图）

• x 轴方向：从 q(x) 分布抽样得到 a。(如果是高斯，就用之前说过的 tricky and faster 的算法更快）
• y 轴方向：从均匀分布（0, kq(a)) 中抽样得到 u。
• 如果刚好落到灰色区域： u > p(a), 拒绝， 否则接受这次抽样
• 重复以上过程

在高维的情况下，Rejection Sampling 会出现两个问题，第一是合适的 q 分布比较难以找到，第二是很难确定一个合理的 k 值。这两个问题会导致拒绝率很高，无用计算增加。

5、重要性抽样(Importance sampling)[2]

Importance Sampling 也是借助了容易抽样的分布 q (proposal distribution)来解决这个问题，直接从公式出发：

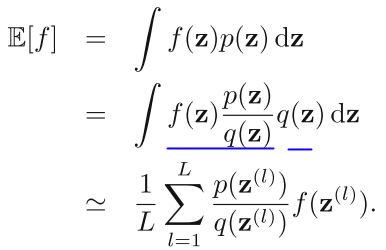
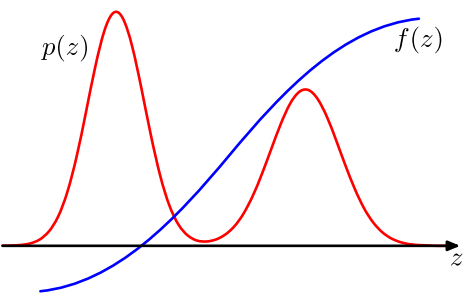
其中，p(z) / q(z) 可以看做 importance weight。我们来考察一下上面的式子，p 和 f 是确定的，我们要确定的是 q。要确定一个什么样的分布才会让采样的效果比较好呢？直观的感觉是，样本的方差越小期望收敛速率越快。比如一次采样是 0, 一次采样是 1000, 平均值是 500,这样采样效果很差，如果一次采样是 499, 一次采样是 501, 你说期望是 500,可信度还比较高。在上式中，我们目标是 p×f/q 方差越小越好，所以 |p×f| 大的地方，proposal distribution q(z) 也应该大。举个稍微极端的例子：

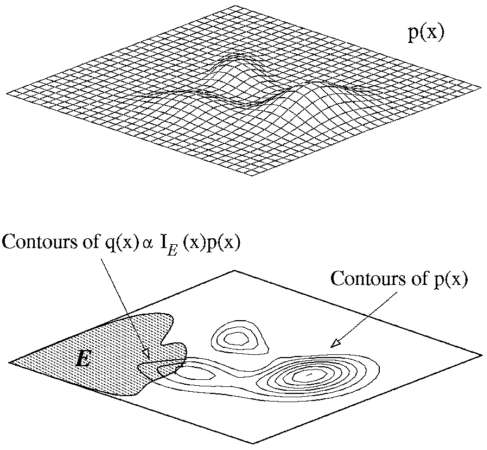
第一个图表示 p 分布， 第二个图的阴影区域 f = 1，非阴影区域 f = 0, 那么一个良好的 q 分布应该在左边箭头所指的区域有很高的分布概率，因为在其他区域的采样计算实际上都是无效的。这表明 Importance Sampling 有可能比用原来的 p 分布抽样更加有效。

但是可惜的是，在高维空间里找到一个这样合适的 q 非常难。即使有 Adaptive importance sampling 和 Sampling-Importance-Resampling(SIR) 的出现，要找到一个同时满足 easy to sample 并且 good approximations 的 proposal distribution, it is often impossible！

6、马尔科夫链，马尔科夫稳态

在讲蒙特卡洛方法之前，必须要先讲一下马尔科夫链；马氏链的数学定义：

也就是说前一个状态只与当前状态有关，而与其他状态无关，Markov Chain 体现的是状态空间的转换关系，下一个状态只决定与当前的状态(可以联想网页爬虫原理，根据当前页面的超链接访问下一个网页)。如下图：

举一个例子，如果当前状态为 u(x) = (0.5, 0.2, 0.3), 那么下一个矩阵的状态就是 u(x)T = (0.18, 0.64, 0.18), 依照这个转换矩阵一直转换下去，最后的系统就趋近于一个稳定状态 (0.22, 0.41, 0.37) (此处只保留了两位有效数字)。而事实证明无论你从那个点出发，经过很长的 Markov Chain 之后都会汇集到这一点。[2]

再举一个例子，社会学家经常把人按其经济状况分成3类：下层(lower-class)、中层(middle-class)、上层(upper-class)，我们用1,2,3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别，那么他的孩子属于下层收入的概率是 0.65, 属于中层收入的概率是 0.28, 属于上层收入的概率是 0.07。事实上，从父代到子代，收入阶层的变化的转移概率如下

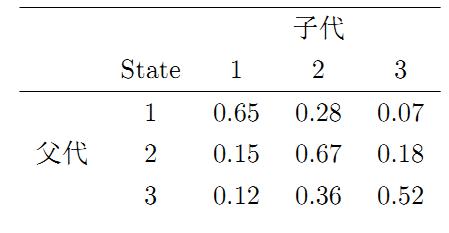
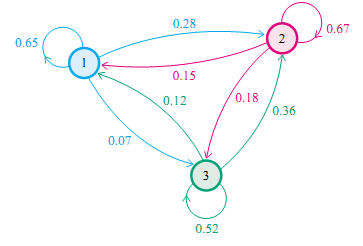
使用矩阵的表示方式，转移概率矩阵记为

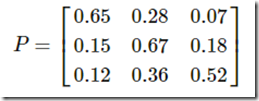
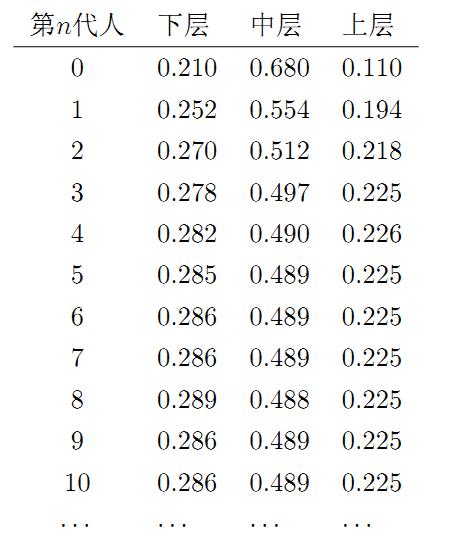
我们发现从第7代人开始，这个分布就稳定不变了，事实上，在这个问题中，从任意初始概率分布开始都会收敛到这个上面这个稳定的结果。

注：要求图是联通的（没有孤立点），同时不存在一个联通的子图是没有对外的出边的（就像黑洞一样）。

这个马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。

对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,， 如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1⋯。

这个绝妙的想法在1953年被 Metropolis想到了，为了研究粒子系统的平稳性质， Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法，即Metropolis算法，并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法，所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中， Metropolis算法也被遴选为二十世纪的十个最重要的算法之一。

我们接下来介绍的MCMC 算法是 Metropolis 算法的一个改进变种，即常用的 Metropolis-Hastings 算法。由上一节的例子和定理我们看到了，马氏链的收敛性质主要由转移矩阵P 决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵P,使得平稳分布恰好是我们要的分布p(x)。如何能做到这一点呢？我们主要使用如下的定理。

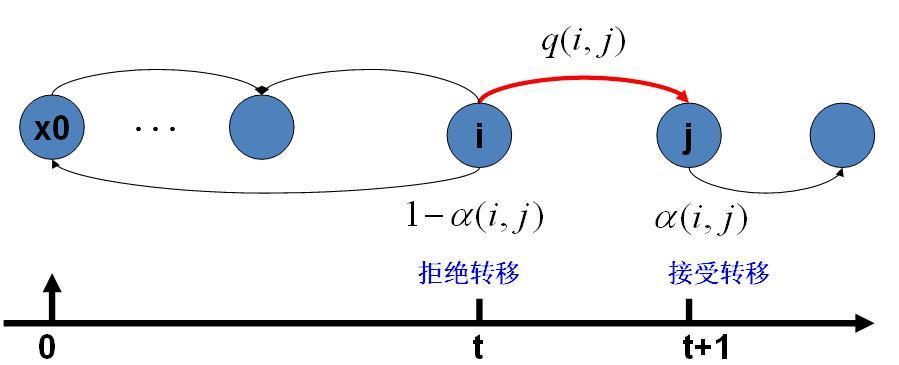
                                    马氏链转移和接受概率

假设我们已经有一个转移矩阵Q(对应元素为q(i,j)), 把以上的过程整理一下，我们就得到了如下的用于采样概率分布p(x)的算法。

8、MCMC——Gibbs Sampling算法

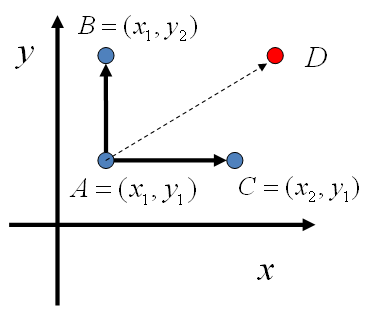
          平面上马氏链转移矩阵的构造

以上算法收敛后，得到的就是概率分布p(x1,x2,⋯,xn)的样本，当然这些样本并不独立，但是我们此处要求的是采样得到的样本符合给定的概率分布，并不要求独立。同样的，在以上算法中，坐标轴轮换采样不是必须的，可以在坐标轴轮换中引入随机性，这时候转移矩阵 Q 中任何两个点的转移概率中就会包含坐标轴选择的概率，而在通常的 Gibbs Sampling 算法中，坐标轴轮换是一个确定性的过程，也就是在给定时刻t，在一根固定的坐标轴上转移的概率是1。