机器学习入门-集成算法(bagging, boosting, stacking)

目的：为了让训练效果更好

bagging：是一种并行的算法，训练多个分类器，取最终结果的平均值 f(x) = 1/M∑fm(x)

boosting: 是一种串行的算法，根据前一次的结果，进行加权来提高训练效果

stacking; 是一种堆叠算法，第一步使用多个算法求出结果，再将结果作为特征输入到下一个算法中训练出最终的预测结果

1.Bagging：全程boostap aggregation(说白了是并行训练一堆分类器)

最典型的算法就是随机森林

随机森林的意思就是特征随机抽取，即每一棵数使用60%的随机特征，数据随机抽取，即每一棵树使用的数据是60%-80%，这样做的目的是为了保证每一棵树的结果在输出是都存在差异。最后对输出的结果求平均

随机森林的优势
               它能处理很高维度的数据，不需要进行特征选择

在训练后他能给出哪些特征的重要性，根据重要性我们也可以进行特征选择

特征重要性的计算方法：如果有特征是A,B,C,D 根据这4个特征求得当前的error，然后对B特征采用随机给定记为B*，对A,B*,C,D求error1，

如果error == error1 ，说明B特征不重要

如果error < error1 说明B特征的重要性很大

当随机森林树的个数超过一定数量后，就会上下浮动

2.Boosting: 是一种串行的算法，通过弱学习器开始加强，通过加权来训练

Fm(x) = Fm-1(x) + argmin(∑L(yi, Fm-1(x) + h(xi) ))   通过前一次的输出结果与目标的残差值，来训练下一颗树的结果（XGboost）

这里介绍一种Adaboost（双加权）

Adaboost 每一次使用一棵树，根据前一颗树的输出结果，来对数据进行加权，比如有5个数据，刚开始的权重都为0.2， 其中第3个数据被判错了，那么第3个数据的权重就为0.6，将经过加权后的数据输入到下一颗树中，再进行训练

根据每一棵树的准确率，再进行权重加权，获得最终的输出结果

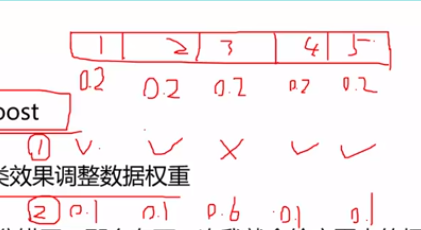
对于数据的权重加和

3.Stacking : 聚合多个分类或回归模型

堆叠，拿来一堆直接上

可以堆叠各种各样的分类器(KNN, SVM, RF)

分阶段进行，第一个阶段可以使用多个分类器获得分类结果，第二阶段将分类结果作为特征输入到一个分类器中，得到最终的结果，缺点就是耗时

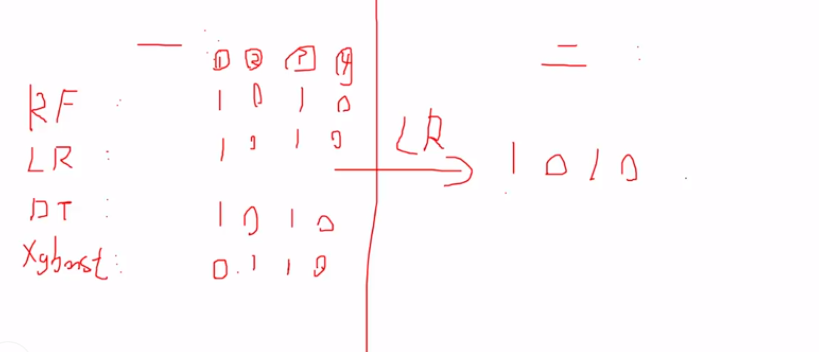
第一阶段                                  第二阶段

RF      ----- 0 1 0 1 --作为特征--输出结果

LR     ------ 1 0 1 0  -----LR-------1 0 1 0

DT     -------1 1 0 1     训练模型

xgboost---- 1 1 0 1