Linear Regression Using Least Squares Method 代码实现

1. 原理

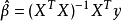
2. Octave

function theta = leastSquaresMethod(X, y)
    theta = pinv(X' * X) * X' * y;

3. Python

# -*- coding:utf8 -*-
import numpy as np

def lse(input_X, _y):
    """
    least squares method
    :param input_X: np.matrix input X
    :param _y: np.matrix y
    """
    return (input_X.T * input_X).I * input_X.T * _y

def test():
    """
    test
    :return: None
    """
    m = np.loadtxt('linear_regression_using_gradient_descent.csv', delimiter=',')
    input_X, y = np.asmatrix(m[:, :-1]), np.asmatrix(m[:, -1]).T
    final_theta = lse(input_X, y)

    t1, t2, t3 = np.array(final_theta).reshape(-1,).tolist()
    print('对测试数据 y = 2 - 4x + 2x^2 求得的参数为: %.3f, %.3f, %.3f\n' % (t1, t2, t3))

if __name__ == "__main__":
    test()

4. C++

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

MatrixXd les(MatrixXd &input_X, MatrixXd &y) {
    return (input_X.transpose() * input_X).inverse() * input_X.transpose() * y;
}

void generate_data(MatrixXd &input_X, MatrixXd &y) {
    ArrayXd v = ArrayXd::LinSpaced(, , );
    input_X.col() = VectorXd::Constant(, , );
    input_X.col() = v.matrix();
    input_X.col() = v.square().matrix();
    y.col() =  * input_X.col() -  * input_X.col() +  * input_X.col();
    y.col() += VectorXd::Random() / ;
  }

int main() {
    MatrixXd input_X(, ), y(, );
    generate_data(input_X, y);
    cout << "对测试数据 y = 2 - 4x + 2x^2 求得的参数为: " << les(input_X, y).transpose() << endl;
}