贪婪算法（Greedy Algorithm）

Greedy Algorithm

《数据结构与算法——C语言描述》

图论涉及的三个贪婪算法

1. Dijkstra 算法
2. Prim 算法
3. Kruskal 算法

Greedy 经典问题：coin change

在每一个阶段，可以认为所作决定是好的，而不考虑将来的后果。

如果不要求最对最佳答案，那么有时用简单的贪婪算法生成近似答案，而不是使用一般说来产生准确答案所需的复杂算法。

所有的调度问题，或者是NP-完全的，或者是贪婪算法可解的。

NP-完全性:

计算复杂性理论中的一个重要概念，它表征某些问题的固有复杂度。一旦确定一类问题具有NP完全性时，就可知道这类问题实际上是具有相当复杂程度的困难问题。

贪心算法是一类算法的统称

10.1.1 一个简单的调度问题

将最后完成时间最小化

这个问题是NP-完全的。因此，将++最后完成时间最小化++显然比++平均完成时间最小++化困难得多。

10.1.2 Huffman 编码

让字符代码的长度从字符到字符是变化不等，同时保证经常出现的字符其代码更短。

最优编码的树将具有的性质：所有结点或者是树叶，或者有两个儿子。

字符代码的长度是否不相同并不要紧，只要没有字符代码是别的字符代码的前缀即可。

基本的问题：

找到总价值（编码总长度）最小的满二叉树。

Huffman 算法

因为每一次合并都不进行全局的考虑，只是选择两棵最小的树，所以该算法是贪心算法。由此可见，贪心算法是一类算法的统称。

在文件压缩这样的应用中，实际上几乎所有的运行时间都花费在读入文件和写文件所需的磁盘 I/O 上。

伪代码

1. 生成 Huffman 树

while(minHeap.size() > 1){
    tree->left  = minHeap.get()
    tree->right = minHeap.get()

    tree->frequence = tree->left->frequence + tree->right->frequence

    minHeap.insert(tree);
}

huffmanTree = minHeap.get();

2. 从 Huffman 树到 Huffman 编码（递归调用）

字符集一般是常数的数量级，所以这里使用递归虽不是最优解，但足矣解此题。

void treeToCode(struct Node* root, Map& codePlan, string& path){
    if(isLeaf(root)){
        //left node
        codePlan[root->character].huffmanCode = path;
    }
    else {
        //internal node
        string leftPath = path + "0";
        treeToCode(root->left, codePlan, leftPath);

        string rightPath = path + "1";
        treeToCode(root->right, codePlan, rightPath);
    }
}

Huffman编码的完整代码实现：

#include <iostream>
#include <string>
#include <queue>
#include <vector>
#include <unordered_map>
#include <utility>

using namespace std;

struct node {
	char c;
	int freq;
	struct node *left;
	struct node *right;
	bool isLeaf;
};

struct Cmp {
	bool operator() (const struct node* lhs, const struct node* rhs){
		return lhs->freq > rhs->freq;
	}
};

struct node* make_node() {
	struct node *p = new node();
	p->left = nullptr;
	p->right = nullptr;
	return p;
}

void treeToCode(struct node* root, unordered_map<char, string>& codePlan, string& path) {
	if (root->left == nullptr && root->right == nullptr) {
		//left node
		codePlan[root->c] = path;
	}
	else {
		//internal node
		string leftPath = path + "0";
		treeToCode(root->left, codePlan, leftPath);

		string rightPath = path + "1";
		treeToCode(root->right, codePlan, rightPath);
	}
}

void huffman(const string &s) {
	unordered_map<char, int> hashmap;

	for (auto c : s) {
		hashmap[c] += 1;
	}

	priority_queue<struct node*, vector<struct node*>, Cmp> heap;

	for (auto e : hashmap) {
		struct node* p = make_node();
		p->c = e.first;
		p->freq = e.second;
		heap.push(p);
	}

	/*while (heap.size()) {
		cout << heap.top()->c << heap.top()->freq << endl;
		heap.pop();
	}*/

	while (heap.size() > 1) {
		struct node* p = make_node();

		p->left = heap.top();
		p->left->freq = heap.top() > 0 ? heap.top() > 0 : heap.top()->left->freq + heap.top()->right->freq;
		heap.pop();

		p->right = heap.top();
		p->right->freq = heap.top() > 0 ? heap.top() > 0 : heap.top()->left->freq + heap.top()->right->freq;
		heap.pop();

		p->freq = p->left->freq + p->right->freq;

		heap.push(p);
	}

	string path;
	unordered_map<char, string> codePlan;
	struct node* root = heap.top();
	treeToCode(root, codePlan, path);
	for (auto e : codePlan) {
		cout << e.first << e.second << endl;
	}
}

int main() {
	string s = "abbcccdddd";
	huffman(s);
	return 0;
}

必须注意的细节

1. 压缩文件的开头必须要传送编码信息，因为否则将不可能译码。
2. 该算法是一个两趟扫描算法。第一趟搜集频率数据，第二遍进行编码。显然这对于处理大型文件的程序来说是不高效的。

10.1.3 近似装箱问题

联机装箱问题：将每一件物品放入一个箱子之后才处理下一件物品。

while (cin >> e) {
    foo(e);
}

脱机装箱问题：做任何事情都需要等到所有的输入数据全部读入之后才进行。

while (cin >> e) {
    v.push_back(e);
}

foo(v);

联机算法

1. 下项适合算法

当处理任何一件物品时，我们检查看它是否能装进刚刚装进物品的同一个箱子中去。如果能就放入该箱子，否则放进新的箱子中。

struct Boxes {
	int rest;
	const int maxQuality;
	vector<int> v;
};

void nextFit(vector<Boxes> &boxes, int curr) {
	if (curr > boxes[0].maxQuality)
		cout << "error : exceed max quality" << endl;

	if (boxes[boxes.size() - 1].rest - curr >= 0){
		boxes[boxes.size() - 1].rest -= curr;
		boxes[boxes.size() - 1].v.push_back(curr);
	}
	else {
		boxes.push_back(Boxes());
		boxes[boxes.size() - 1].rest -= curr;
		boxes[boxes.size() - 1].v.push_back(curr);
	}
}

2.首次适合算法

依次扫描这些箱子，但把新的一项物品放入足够盛下它的第一个箱子中。

struct Boxes {
	int rest;
	const int maxQuality;
	vector<int> v;
};

void firstFit(vector<Boxes> &boxes, int curr) {
	if (curr > boxes[0].maxQuality)
		cout << "error : exceed max quality" << endl;

	for (auto &box : boxes) {
		if (box.rest - curr >= 0) {
			box.rest -= curr;
			box.v.push_back(curr);
			return;
		}
	}

	boxes.push_back(Boxes());
	boxes[boxes.size() - 1].rest -= curr;
	boxes[boxes.size() - 1].v.push_back(curr);
}

3. 最佳适合算法

把新物品放入所有的箱子当中，能够容纳它并且最满的箱子中。

struct Boxes {
	int rest;
	const int maxQuality;
	vector<int> v;
};

void bestFit(vector<Boxes> &boxes, int curr) {
	if (curr > boxes[0].maxQuality) {
		cout << "error : out of max quality" << endl;
		return;
	}

	size_t fitNo = -1;
	int fitRest = boxes[0].maxQuality;

	for (size_t i = 0; i < boxes.size(); i++) {
		int curRest = boxes[i].rest - curr;

		if (fitRest > curRest && curRest >= 0) {
			fitRest = curRest;
			fitNo = i;
		}
	}

	if (fitNo == -1 && fitRest == boxes[0].maxQuality) {
		boxes.push_back(Boxes());
		boxes[boxes.size() - 1].rest -= curr;
		boxes[boxes.size() - 1].v.push_back(curr);
	}
	else {
		boxes[fitNo].v.push_back(curr);
		boxes[fitNo].rest -= curr;
	}
}

脱机算法

围绕这个问题的自然方法是将各项物品排序，把最大的物品放在最先。此时应用首次适合算法或最佳适合算法，分别得到首次适合递减算法（first fit decreasing）和最佳适合递减算法（best fit decreasing）。

struct Boxes {
	int rest;
	const int maxQuality;
	vector<int> v;
};

void firstFit(vector<Boxes> &boxes, int curr) {
	if (curr > boxes[0].maxQuality)
		cout << "error : exceed max quality" << endl;

	for (auto &box : boxes) {
		if (box.rest - curr >= 0) {
			box.rest -= curr;
			box.v.push_back(curr);
			return;
		}
	}

	boxes.push_back(Boxes());
	boxes[boxes.size() - 1].rest -= curr;
	boxes[boxes.size() - 1].v.push_back(curr);
}

void firstFitNonIncreasing(vector<Boxes>& boxes, vector<int>& v) {
	sort(v.begin(), v.end(), greater<int>());
	for (auto e : v)
		firstFit(boxes, e);
}

int main() {
	firstFitNonIncreasing(boxes, input);
}

---

《算法之美》

7.4.1 哈夫曼编码

哈夫曼使用自底向上的方法构建二叉树。

在 JPEG 图像压缩方式中，就用到了哈夫曼编码。

哈夫曼编码是一种不等长德编码，其基本原理是频繁使用的数据用较短的代码代替。（离散性）

哈夫曼编码具有即时性和唯一可译性。

哈夫曼树就是带权路径最小的二叉树。树的带权路径长度（WPL，Weight Path Length）是树中所有叶子结点的带权路径长度之和。

通过将权值大的外结点调整到离根结点较近的位置来得到最小路径长度。

7.4.2 构造哈夫曼树

7.4.3 哈夫曼编码的实现

哈夫曼编码是无前缀编码。

产生哈夫曼编码需要对原始数据扫描两遍。第1遍扫描时为了要统计出原始数据中每个值出现的频率，第2遍是建立哈夫曼树并进行编码。

缺点与不足

1. 哈夫曼编码的码字长度参差不齐，硬件实现不方便
2. 码字在存储或传输过程中，如果出现误码时，可能引起误码的连续传播
3. 对数据进行解码时，必须参照哈夫曼编码表

---

《算法的乐趣》

算法设计的常用思想

算法是一次智力活动的结果，但并不是毫无章法的爆发，它应该是遵循一定规律的智力活动。

首先，它需要一些基础知识作为着力点。比如数据结构。

其次，对问题域做高度概括并抽象出问题的精确描述。建立数学模型。

最后，选择一些常用的模式和原则，有人称之为算法设计模式或算法设计思想。

3.1 贪婪法

寻找最优解的问题的常用办法。将求解过程分成若干步骤，并在每个步骤都应用贪心原则——选取当前状态下，最好或者最优的选择。

贪婪法、动态规划和分治法一样，都需要对问题进行分解，定义最优解的子结构。

因为不进行回溯处理，贪婪法只在很少的情况下可以得到真正的最优解，比如最短路径问题、图的最小生成树问题。

通常最为其他算法的辅助算法来使用。

3.1.1 贪婪法的基本思想

三个步骤

1. 建立数学模型
2. 分解为子问题
3. 用子问题的局部最优解迭代出全局最优解

关于“找零问题”，子问题的最优解结构就是在之前的步骤中，给已经选好的硬币加上当前选择的一枚硬币。

但是，同样是“找零问题”，贪婪法在很多情况下得到的只是近似最优解。

---

《数据结构、算法与应用（C++语言描述）》

17.1 最优化问题

限制条件、优化函数、可行解、最优解

每个最优化问题都包含一组限制条件和一个优化函数。

符合限制条件的问题求解方案称为可行解。

使优化函数可能取得最佳值的可行解称为最优解。

用数学语言来表达问题是精确的，它可以清楚地说明求解问题的程序。

17.2 贪婪算法思想

在贪婪算法中，我们要逐步构造一个最优解。

每一步我们都在一定的标准下，作出一个最优决策。

例17-4[找零钱]

struct Stratrgy{
	map<int, int, greater<int>> m;

	Stratrgy(initializer_list<int> l) {
		for (auto e : l) {
			m[e] = 0;
		}
	}
};

void change(int total, Stratrgy& s) {
	for (auto &e : s.m) {
		int n = 0;
		while ((total - (n+1) * e.first) >= 0){
			n++;
		}

		total -= n*e.first;
		e.second = n;
	}
}

void printStrategy(const Stratrgy& s) {
	for (auto e : s.m) {
		cout << e.first << " " << e.second << endl;
	}
}

int main() {
	Stratrgy s({25, 10, 5, 1});

	change(41, s);
	printStrategy(s);

	printStrategy(s2);

	return 0;
}

得到的是近似最优解

例17-5[机器调度]

按照任务起始时间的非递减顺序

采用一个复杂性为 O(N * logN)的排序算法（如堆排序），按 Si 的非递减次序排列排序，然后使用一个关于“旧”机器可用时刻的最小堆。

struct Task {
	Task(char id, int start, int finish) :id(id), s(start), f(finish) {}
	char id;
	int s;
	int f;
};

struct Machine {
	Machine(size_t id) : id(id), u(0), v() {}
	Machine() {}
	size_t id;
	int u;
	vector<char> v;
};

vector<Machine> schedule(vector<Task>& tasks) {
	sort(tasks.begin(), tasks.end(),
		[](const Task& lhs, const Task& rhs) {
		return lhs.s < rhs.s;
	});

	auto machineCmp = [](const Machine& lhs, const Machine& rhs) {return lhs.u > rhs.u; };

	priority_queue<Machine, vector<Machine>, decltype(machineCmp)> machines(machineCmp);

	for (auto e : tasks) {
		Machine m;

		if (!machines.empty() && e.s >= machines.top().u) {
			m = machines.top();
			machines.pop();
		}
		else {
			m.id = machines.size() + 1;
		}

		m.u = e.f;
		m.v.push_back(e.id);
		machines.push(m);
	}

	vector<Machine> v;
	while (!machines.empty()){
		v.push_back(machines.top());
		machines.pop();
	}

	return v;
}

int main() {
	vector<Task> v = {
		{ 'a', 0, 2},
		{ 'b', 3, 7 },
		{ 'c', 4, 7 },
		{ 'd', 9, 11 },
		{ 'e', 7, 10 },
		{ 'f', 1, 5 },
		{ 'g', 6, 8 }
	};

	vector<Machine> scheduling = schedule(v);

	for (auto machine : scheduling) {
		cout << machine.id << endl;
		for (auto e : machine.v) {
			cout << e << " ";
		}
		cout << endl;
	}

	return 0;
}

17-3-2 0/1背包问题

问题的公式描述

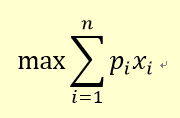
约束条件

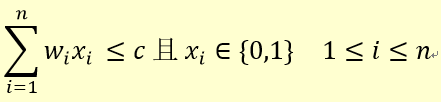
货物装箱与 0/1 背包的对比

货物装箱 Wi C

0/1 背包 Wi Pi C

总结

0/1 背包问题实际上是一个一般化的货箱装载问题，只是从每个货箱所获得的价值不同。

0/1 背包问题是一个 NP-复杂问题

---

《算法设计与分析基础》

穷举查找

对于背包问题，穷举查找算法对于任何输入都是非常低效率的。

旅行商问题和背包问题是NP困难问题中最著名的例子。

对于NP困难问题，目前没有已知的效率可以用多项式来表示的算法。

本书对于“背包问题”的分类与学习顺序

穷尽查找 -> DP -> 分支界定法 -> NP困难问题的近似解法