1110 Complete Binary Tree （25 分）

1110 Complete Binary Tree （25 分）

Given a tree, you are supposed to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤20) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a -will be put at the position. Any pair of children are separated by a space.

Output Specification:

For each case, print in one line YES and the index of the last node if the tree is a complete binary tree, or NO and the index of the root if not. There must be exactly one space separating the word and the number.

Sample Input 1:

9
7 8
- -
- -
- -
0 1
2 3
4 5
- -
- -

Sample Output 1:

YES 8

Sample Input 2:

8
- -
4 5
0 6
- -
2 3
- 7
- -
- -

Sample Output 2:

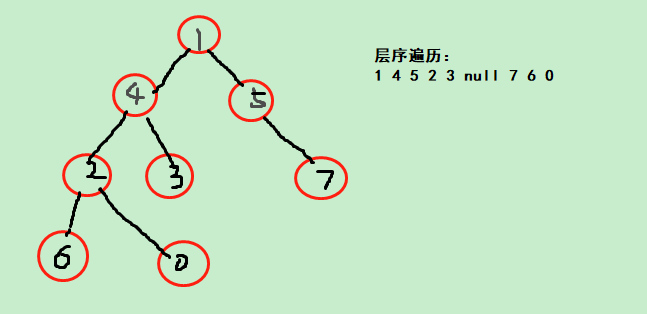
NO 1

分析：判断是否是完全二叉树。先求根节点，可以设置一个数组child，如果输入过程中如果该结点被当做孩子节点那它一定不是根节点，输入完毕后从头开始遍历child数组，第一个是false的child[i]跳出，i就是根节点。那么如何判断是完全二叉树呢？这里提供两种方法。

1、层序遍历，每次把空节点也Push进队列中，完全二叉树层序遍历过程中，如果遇到空节点了，说明一定已经遍历完非空节点；而对非完全二叉树，如果遇到空节点了，后面还必定有非空节点。于是遍历过程中用一个变量统计已入队过的节点数量。

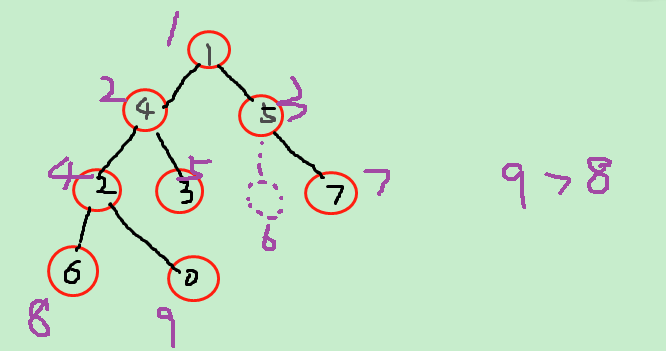
2、递归求最大下标值，完全二叉树中，最大下标值=最大结点数（起始为1）； 而非完全二叉树中，最大下标值>最大结点数

 代码分别如下：

 /**
 * Copyright(c)
 * All rights reserved.
 * Author : Mered1th
 * Date : 2019-02-26-21.04.42
 * Description : A1110
 */
 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<string>
 #include<unordered_set>
 #include<map>
 #include<vector>
 #include<set>
 #include<queue>
 using namespace std;
 struct Node{
     int l,r;
 }node[];
 ]={false};
 ,n;
 bool isCBT(int root){
     ;
     queue<int>q;
     q.push(root);
     while(!q.empty()){
         int top=q.front();
         q.pop();
         ){
             maxd=top;
             cnt++;
             q.push(node[top].l);
             q.push(node[top].r);
         }
         else{
             if(cnt==n) return true;
             else return false;
         }
     }
 }

 int main(){
 #ifdef ONLINE_JUDGE
 #else
     freopen("1.txt", "r", stdin);
 #endif
     cin>>n;
     string a,b;
     ;i<n;i++){
         cin>>a>>b;
         ]=='-'){
             node[i].l=-;
         }
         else{
             node[i].l=stoi(a);
             child[stoi(a)]=true;
         }
         ]=='-'){
             node[i].r=-;
         }
         else{
             node[i].r=stoi(b);
             child[stoi(b)]=true;
         }
     }
     int root;
     ;i<n;i++){
         if(child[i]==false){
             root=i;
             break;
         }
     }
     if(isCBT(root)) printf("YES %d",maxd);
     else printf("NO %d",root);
     ;
 }

这里利用了二叉树静态存储的性质，即父节点和叶子节点之间的关系。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<queue>
 using namespace std;
 struct node{
     int data;
     int l,r;
 }Node[];
 ,n;
 ]={false};
 /*void LayerOrder(int root){
     queue<int> Q;
     Q.push(root);
     while(!Q.empty()){
         int now=Q.front();
         Q.pop();
         if(Node[now].l!=-1){
             if(Node[now].r!=-1){
                 cnt++;
                 Q.push(Node[now].l);
             }
             else{
                 cnt++;
             }
         }
         if(Node[now].r!=-1){
             if(Node[now].l!=-1){
                 cnt++;
                 Q.push(Node[now].r);
             }
             else{
                 cnt++;
             }
         }
     }
 }
 */
 ,ans;
 void dfs(int root,int index){
     //求出最大下标值，如果下标值等于最大节点数-1则说明是完全二叉树，若大于最大结点数-1则非完全二叉树
     if(index>maxn){
         maxn=index;
         ans=root;
     }
     ) dfs(Node[root].l,index*);
     ) dfs(Node[root].r,index*+);
 }
 int main(){
 #ifdef ONLINE_JUDGE
 #else
     freopen("1.txt", "r", stdin);
 #endif
     cin>>n;
     string t1,t2;
     ;i<n;i++){
         cin>>t1>>t2;
         Node[i].data=i;
         if(t1=="-"){
             Node[i].l=-;
         }
         else{
             Node[i].l=stoi(t1);
             hashtable[stoi(t1)]=true;
         }
         if(t2=="-"){
             Node[i].r=-;
         }
         else{
             Node[i].r=stoi(t2);
             hashtable[stoi(t2)]=true;
         }
     }
     int i;
     ;i<n;i++){
         if(hashtable[i]==false) break;
     }
     dfs(i,);
     if(maxn==n){
         cout<<"YES "<<ans;
     }
     else{
         cout<<"NO "<<i;
     }
     ;
 }