一种新型聚类算法(Clustering by fast search and find of density peaksd)

最近在学习论文的时候发现了在science上发表的关于新型的基于密度的聚类算法

Kmean算法有很多不足的地方，比如k值的确定，初始结点选择，而且还不能检测费球面类别的数据分布，对于第二个问题，提出了Kmean++，而其他不足还没有解决，dbscan虽然可以对任意形状分布的进行聚类，但是必须指定一个密度阈值，从而去除低于此密度阈值的噪音点，这篇文章解决了这些不足。

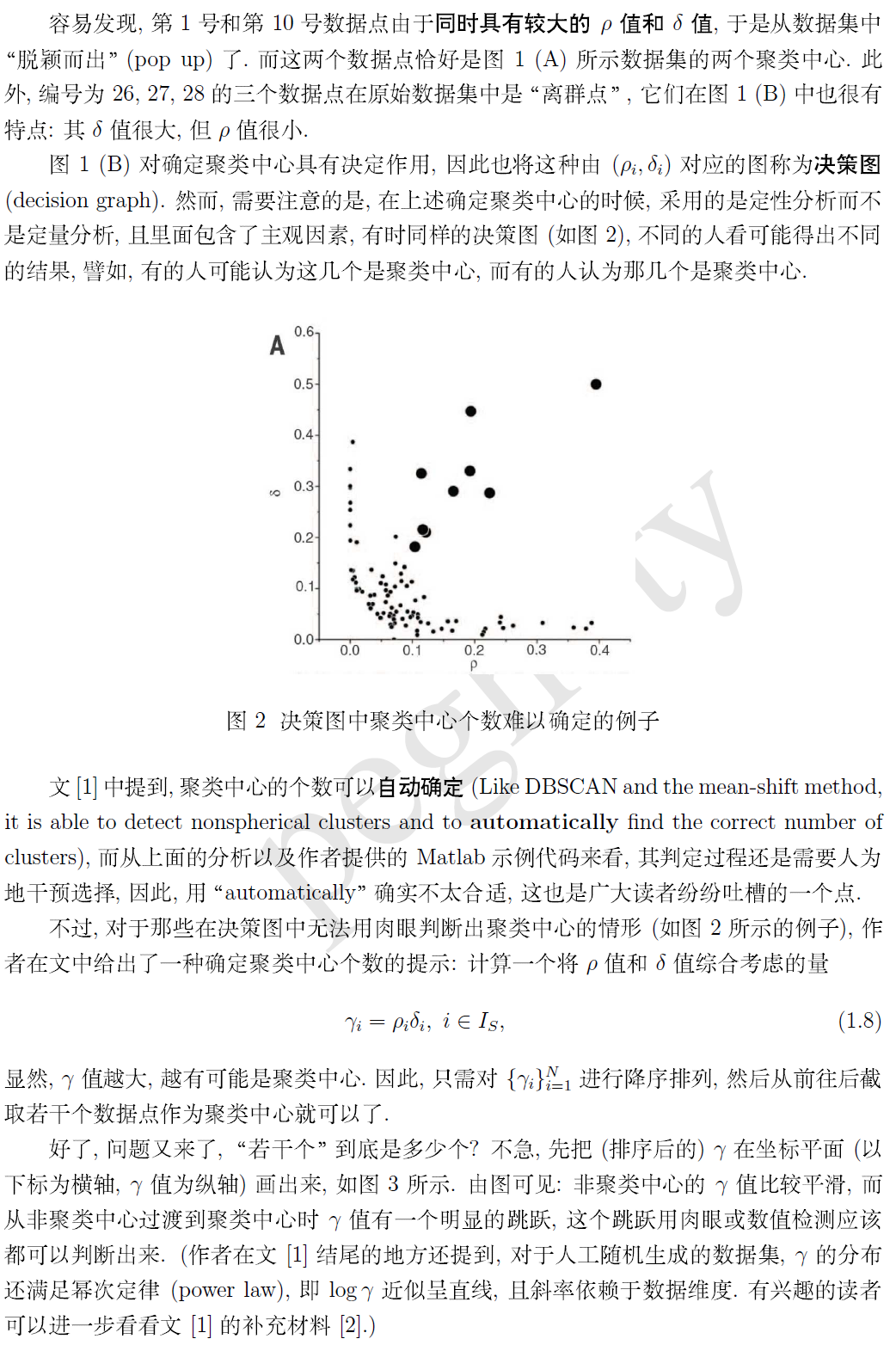
本文提出的聚类算法的核心思想在于，对聚类中心的刻画上，而且认为聚类中心同时具有以下两种特点：

• 本身的密度大，即它被密度均不超过它的邻居包围
• 与其他密度更大的数据点之间的“距离”相对更大

 

通俗的理解为：给一个节点求与其距离小于一个值的节点的个数，用这个个数表示节点的密度，此时求出来的就是节点的局部密度，

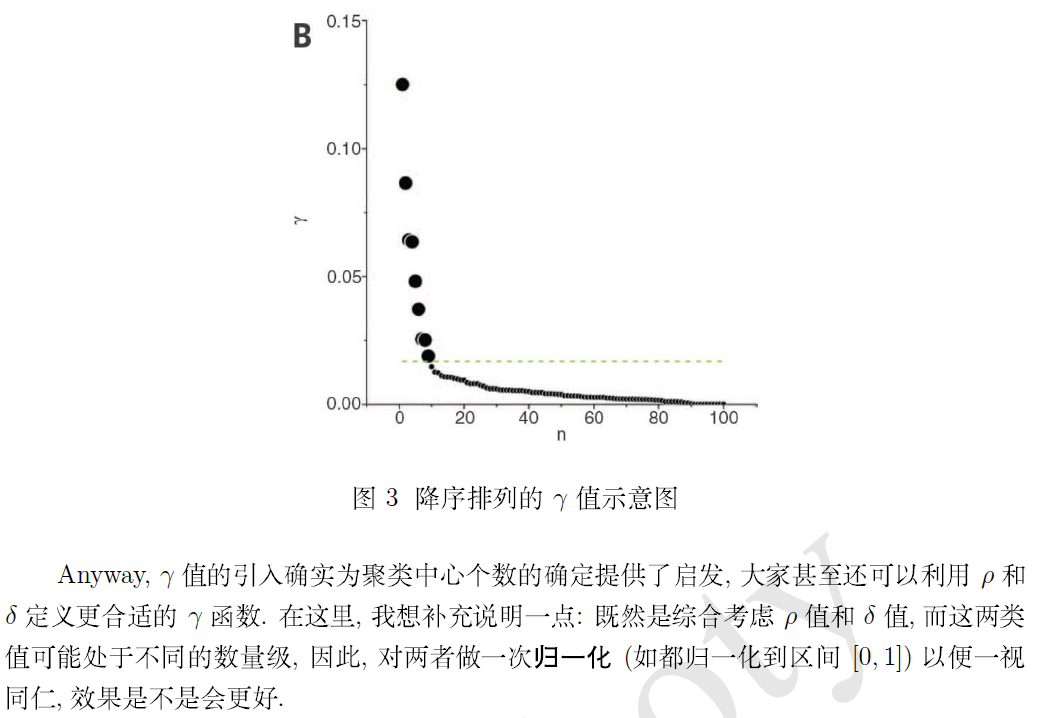
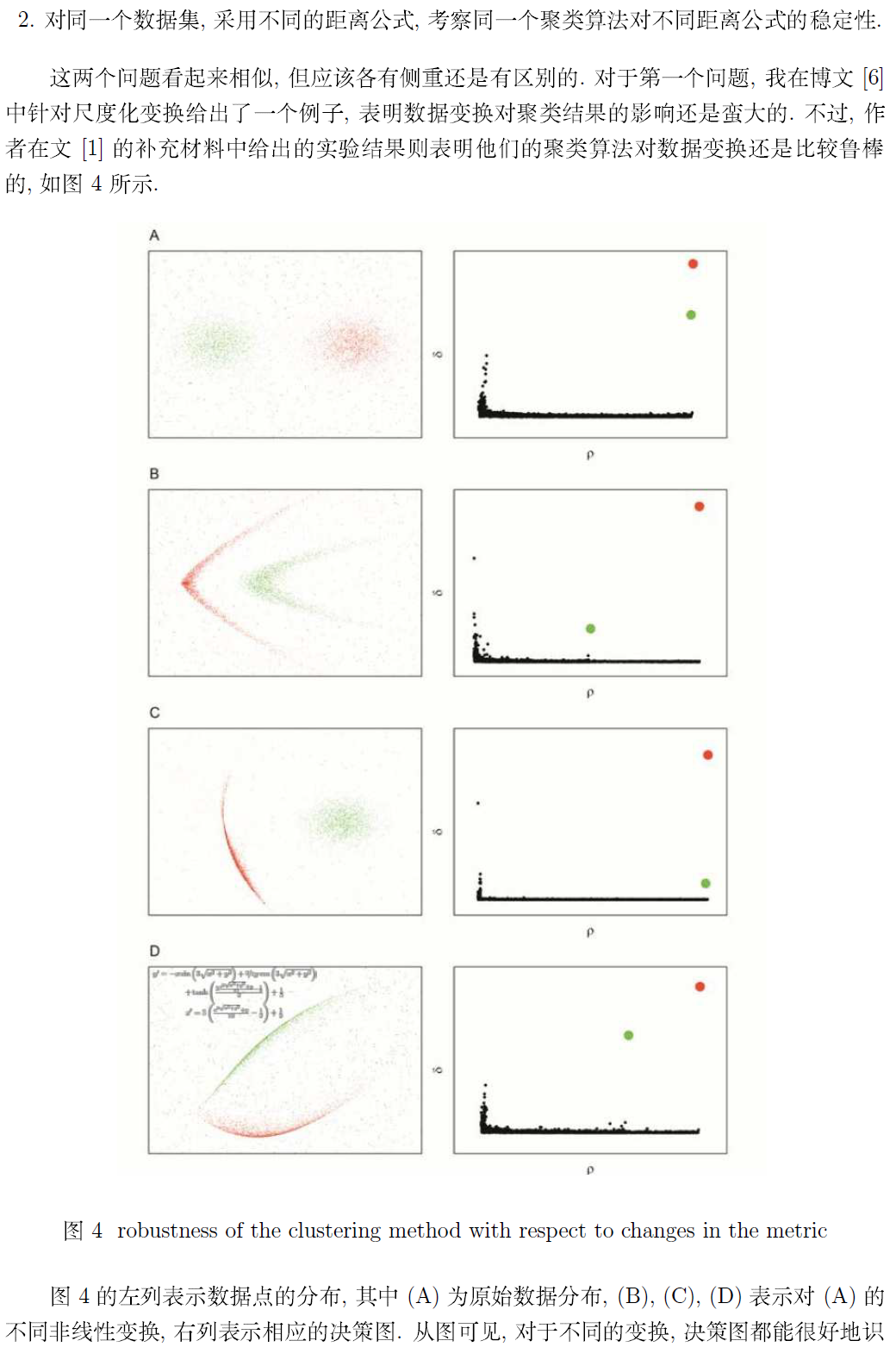
经过上边的过程，每个点都可以找到两个距离与之对应，然后建立一个二维坐标轴，在坐标轴上把图形画出来，如下图

最后，附上作者在补充材料里提供的 Matlab 示例程序 （加了适当的代码注释）

clear all
close all
disp('The only input needed is a distance matrix file')
disp('The format of this file should be: ')
disp('Column 1: id of element i')
disp('Column 2: id of element j')
disp('Column 3: dist(i,j)')  
 
%% 从文件中读取数据
mdist=input('name of the distance matrix file (with single quotes)?\n');
disp('Reading input distance matrix')
xx=load(mdist);
ND=max(xx(:,));
NL=max(xx(:,));
if (NL>ND)
  ND=NL;  %% 确保 DN 取为第一二列最大值中的较大者，并将其作为数据点总数
end  
 
N=size(xx,); %% xx 第一个维度的长度，相当于文件的行数（即距离的总个数）  
 
%% 初始化为零
for i=:ND
  for j=:ND
    dist(i,j)=;
  end
end  
 
%% 利用 xx 为 dist 数组赋值，注意输入只存了 0.5*DN(DN-) 个值，这里将其补成了满矩阵
%% 这里不考虑对角线元素
for i=:N
  ii=xx(i,);
  jj=xx(i,);
  dist(ii,jj)=xx(i,);
  dist(jj,ii)=xx(i,);
end  
 
%% 确定 dc  
 
percent=2.0;
fprintf('average percentage of neighbours (hard coded): %5.6f\n', percent);  
 
position=round(N*percent/); %% round 是一个四舍五入函数
sda=sort(xx(:,)); %% 对所有距离值作升序排列
dc=sda(position);  
 
%% 计算局部密度 rho (利用 Gaussian 核)  
 
fprintf('Computing Rho with gaussian kernel of radius: %12.6f\n', dc);  
 
%% 将每个数据点的 rho 值初始化为零
for i=:ND
  rho(i)=.;
end  
 
% Gaussian kernel
for i=:ND-
  for j=i+:ND
     rho(i)=rho(i)+exp(-(dist(i,j)/dc)*(dist(i,j)/dc));
     rho(j)=rho(j)+exp(-(dist(i,j)/dc)*(dist(i,j)/dc));
  end
end  
 
% "Cut off" kernel
%for i=:ND-
%  for j=i+:ND
%    if (dist(i,j)<dc)
%       rho(i)=rho(i)+.;
%       rho(j)=rho(j)+.;
%    end
%  end
%end  
 
%% 先求矩阵列最大值，再求最大值，最后得到所有距离值中的最大值
maxd=max(max(dist));   
 
%% 将 rho 按降序排列，ordrho 保持序
[rho_sorted,ordrho]=sort(rho,'descend');  
 
%% 处理 rho 值最大的数据点
delta(ordrho())=-.;
nneigh(ordrho())=;  
 
%% 生成 delta 和 nneigh 数组
for ii=:ND
   delta(ordrho(ii))=maxd;
   for jj=:ii-
     if(dist(ordrho(ii),ordrho(jj))<delta(ordrho(ii)))
        delta(ordrho(ii))=dist(ordrho(ii),ordrho(jj));
        nneigh(ordrho(ii))=ordrho(jj);
        %% 记录 rho 值更大的数据点中与 ordrho(ii) 距离最近的点的编号 ordrho(jj)
     end
   end
end  
 
%% 生成 rho 值最大数据点的 delta 值
delta(ordrho())=max(delta(:));  
 
%% 决策图  
 
disp('Generated file:DECISION GRAPH')
disp('column 1:Density')
disp('column 2:Delta')  
 
fid = fopen('DECISION_GRAPH', 'w');
for i=:ND
   fprintf(fid, '%6.2f %6.2f\n', rho(i),delta(i));
end  
 
%% 选择一个围住类中心的矩形
disp('Select a rectangle enclosing cluster centers')  
 
%% 每台计算机，句柄的根对象只有一个，就是屏幕，它的句柄总是
%% >> scrsz = get(,'ScreenSize')
%% scrsz =
%%
%%  和  就是你设置的计算机的分辨率，scrsz() 就是 ，scrsz() 就是
scrsz = get(,'ScreenSize');  
 
%% 人为指定一个位置，感觉就没有那么 auto 了 :-)
figure('Position',[  scrsz()/. scrsz()/1.3]);  
 
%% ind 和 gamma 在后面并没有用到
for i=:ND
  ind(i)=i;
  gamma(i)=rho(i)*delta(i);
end  
 
%% 利用 rho 和 delta 画出一个所谓的“决策图”  
 
subplot(,,)
tt=plot(rho(:),delta(:),'o','MarkerSize',,'MarkerFaceColor','k','MarkerEdgeColor','k');
title ('Decision Graph','FontSize',15.0)
xlabel ('\rho')
ylabel ('\delta')  
 
subplot(,,)
rect = getrect();
%% getrect 从图中用鼠标截取一个矩形区域， rect 中存放的是
%% 矩形左下角的坐标 (x,y) 以及所截矩形的宽度和高度
rhomin=rect();
deltamin=rect(); %% 作者承认这是个 error，已由  改为  了!  
 
%% 初始化 cluster 个数
NCLUST=;  
 
%% cl 为归属标志数组，cl(i)=j 表示第 i 号数据点归属于第 j 个 cluster
%% 先统一将 cl 初始化为 -
for i=:ND
  cl(i)=-;
end  
 
%% 在矩形区域内统计数据点（即聚类中心）的个数
for i=:ND
  if ( (rho(i)>rhomin) && (delta(i)>deltamin))
     NCLUST=NCLUST+;
     cl(i)=NCLUST; %% 第 i 号数据点属于第 NCLUST 个 cluster
     icl(NCLUST)=i;%% 逆映射,第 NCLUST 个 cluster 的中心为第 i 号数据点
  end
end  
 
fprintf('NUMBER OF CLUSTERS: %i \n', NCLUST);  
 
disp('Performing assignation')  
 
%% 将其他数据点归类 (assignation)
for i=:ND
  if (cl(ordrho(i))==-)
    cl(ordrho(i))=cl(nneigh(ordrho(i)));
  end
end
%% 由于是按照 rho 值从大到小的顺序遍历,循环结束后, cl 应该都变成正的值了.   
 
%% 处理光晕点，halo这段代码应该移到 if (NCLUST>) 内去比较好吧
for i=:ND
  halo(i)=cl(i);
end  
 
if (NCLUST>)  
 
  % 初始化数组 bord_rho 为 ,每个 cluster 定义一个 bord_rho 值
  for i=:NCLUST
    bord_rho(i)=.;
  end  
 
  % 获取每一个 cluster 中平均密度的一个界 bord_rho
  for i=:ND-
    for j=i+:ND
      %% 距离足够小但不属于同一个 cluster 的 i 和 j
      if ((cl(i)~=cl(j))&& (dist(i,j)<=dc))
        rho_aver=(rho(i)+rho(j))/.; %% 取 i,j 两点的平均局部密度
        if (rho_aver>bord_rho(cl(i)))
          bord_rho(cl(i))=rho_aver;
        end
        if (rho_aver>bord_rho(cl(j)))
          bord_rho(cl(j))=rho_aver;
        end
      end
    end
  end  
 
  %% halo 值为  表示为 outlier
  for i=:ND
    if (rho(i)<bord_rho(cl(i)))
      halo(i)=;
    end
  end  
 
end  
 
%% 逐一处理每个 cluster
for i=:NCLUST
  nc=; %% 用于累计当前 cluster 中数据点的个数
  nh=; %% 用于累计当前 cluster 中核心数据点的个数
  for j=:ND
    if (cl(j)==i)
      nc=nc+;
    end
    if (halo(j)==i)
      nh=nh+;
    end
  end  
 
  fprintf('CLUSTER: %i CENTER: %i ELEMENTS: %i CORE: %i HALO: %i \n', i,icl(i),nc,nh,nc-nh);  
 
end  
 
cmap=colormap;
for i=:NCLUST
   ic=int8((i*.)/(NCLUST*.));
   subplot(,,)
   hold on
   plot(rho(icl(i)),delta(icl(i)),'o','MarkerSize',,'MarkerFaceColor',cmap(ic,:),'MarkerEdgeColor',cmap(ic,:));
end
subplot(,,)
disp('Performing 2D nonclassical multidimensional scaling')
Y1 = mdscale(dist, , 'criterion','metricstress');
plot(Y1(:,),Y1(:,),'o','MarkerSize',,'MarkerFaceColor','k','MarkerEdgeColor','k');
title ('2D Nonclassical multidimensional scaling','FontSize',15.0)
xlabel ('X')
ylabel ('Y')
for i=:ND
 A(i,)=.;
 A(i,)=.;
end
for i=:NCLUST
  nn=;
  ic=int8((i*.)/(NCLUST*.));
  for j=:ND
    if (halo(j)==i)
      nn=nn+;
      A(nn,)=Y1(j,);
      A(nn,)=Y1(j,);
    end
  end
  hold on
  plot(A(:nn,),A(:nn,),'o','MarkerSize',,'MarkerFaceColor',cmap(ic,:),'MarkerEdgeColor',cmap(ic,:));
end  
 
%for i=:ND
%   if (halo(i)>)
%      ic=int8((halo(i)*.)/(NCLUST*.));
%      hold on
%      plot(Y1(i,),Y1(i,),'o','MarkerSize',,'MarkerFaceColor',cmap(ic,:),'MarkerEdgeColor',cmap(ic,:));
%   end
%end
faa = fopen('CLUSTER_ASSIGNATION', 'w');
disp('Generated file:CLUSTER_ASSIGNATION')
disp('column 1:element id')
disp('column 2:cluster assignation without halo control')
disp('column 3:cluster assignation with halo control')
for i=:ND
   fprintf(faa, '%i %i %i\n',i,cl(i),halo(i));
end  

参考：http://blog.csdn.net/aimatfuture/article/details/39405261

http://blog.csdn.net/zxdxyz/article/details/40655231