HDU 1542 - Atlantis - [线段树+扫描线]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1542

Time Limit: 2000/1000 MS (Java/Others)　　Memory Limit: 65536/32768 K (Java/Others)

Problem Description

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.

 

Input

The input file consists of several test cases. Each test case starts with a line containing a single integer n (1<=n<=100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0<=x1<x2<=100000;0<=y1<y2<=100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.

The input file is terminated by a line containing a single 0. Don’t process it.

 

Output

For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.

Output a blank line after each test case.

 

Sample Input

2

10 10 20 20

15 15 25 25.5

0

 

Sample Output

Test case #1

Total explored area: 180.00

题意：

给出n个矩形的左下角和右上角坐标，保证矩形面积大于零，要求n个矩形所覆盖的整个图形的面积。

题解：

属于线段树配合扫描线的模板题，

转载自https://blog.csdn.net/konghhhhh/article/details/78236036的线段树+扫描线基本原理：

---

假想有一条扫描线，从左往右（从右往左），或者从下往上（从上往下）扫描过整个多边形（或者说畸形……多个矩形叠加后的那个图形）。

如果是竖直方向上扫描，则是离散化横坐标，如果是水平方向上扫描，则是离散化纵坐标。下面的分析都是离散化横坐标的，并且从下往上扫描的。

扫描之前还需要做一个工作，就是保存好所有矩形的上下边，并且按照它们所处的高度进行排序，另外如果是上边我们给他一个值$-1$，下边给他一个值$1$，我们用一个结构体来保存所有的上下边：

struct Segment
{
    double l,r,h; //l和r表示这条上下边的左右坐标，h是这条边所处的高度
    int f; //所赋的值，1或-1
}

接着扫描线从下往上扫描，每遇到一条上下边就停下来，将这条线段投影到总区间上（总区间就是整个多边形横跨的长度），这个投影对应的其实是个插入和删除线段操作。

还记得给他们赋的值$1$或$-1$吗，下边是$1$，扫描到下边的话相当于往总区间插入一条线段，上边是$-1$，扫描到上边相当于在总区间删除一条线段（如果说插入删除比较抽象，那么就直白说，扫描到下边，投影到总区间，对应的那一段的值都要增$1$，扫描到上边对应的那一段的值都要减$1$，如果总区间某一段的值为$0$，说明其实没有线段覆盖到它，为正数则有，那会不会为负数呢？是不可能的，可以自己思考一下）。

每扫描到一条上下边后并投影到总区间后，就判断总区间现在被覆盖的总长度，然后用下一条边的高度减去当前这条边的高度，乘上总区间被覆盖的长度，就能得到一块面积，并依此做下去，就能得到最后的面积。

---

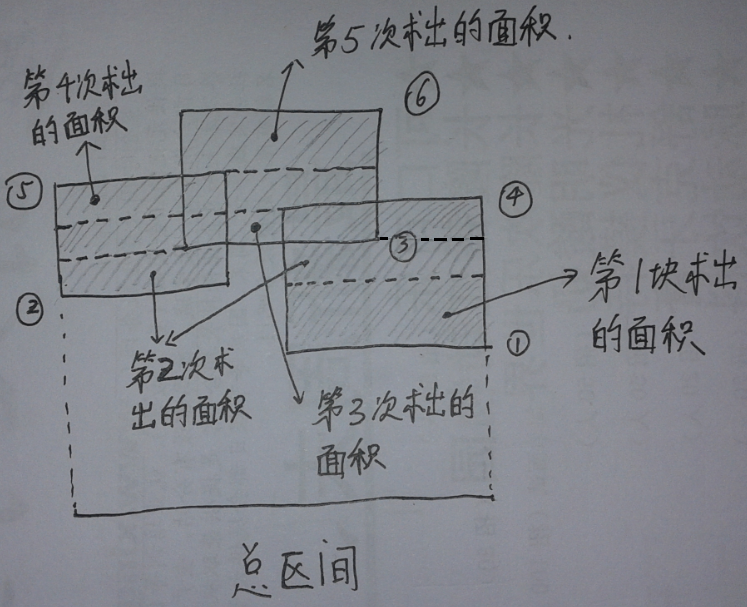
当然了，我们知道，线段树维护的是点，而这里我们要维护的是连续的区间，

因此我们给每个点赋予新的意义：对于第 i 个点，其代表区间 [ i , i+1 )，

然后，本题对横轴坐标进行去重离散化，假设最后剩下size个横坐标，存储在数组 x[1~size]中，那么我们线段树就从 点0 到 点size-1 建树，这样就能维护整个总区间，

同时我们也需要对线段树进行一定的修改，体现在代码中。

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;

const int maxn=;

int n;

vector<double> x;
inline int getID(double val){return lower_bound(x.begin(),x.end(),val)-x.begin();}

struct Segment
{
    double l,r;
    double h;
    int flag;
}segment[maxn];
bool cmp(Segment a,Segment b){return a.h<b.h;}

/********************************* Segment Tree - st *********************************/
struct Node{
    int l,r;
    int s;
    double len;
}node[*maxn];
void pushup(int rt)
{
    if(node[rt].s) node[rt].len=x[(node[rt].r+)]-x[(node[rt].l)];
    else if(node[rt].l==node[rt].r) node[rt].len=;
    else node[rt].len=node[rt*].len+node[rt*+].len;
}
void build(int rt,int l,int r)
{
    if(l>r) return;
    node[rt].l=l; node[rt].r=r;
    node[rt].s=; node[rt].len=;
    if(l==r) return;
    else
    {
        int mid=l+(r-l)/;
        build(rt*,l,mid);
        build(rt*+,mid+,r);
        pushup(rt);
    }
}
void update(int root,int st,int ed,int val)
{
    if(st>node[root].r || ed<node[root].l) return;
    if(st<=node[root].l && node[root].r<=ed)
    {
        node[root].s+=val;
        pushup(root);
    }
    else
    {
        update(root*,st,ed,val);
        update(root*+,st,ed,val);
        pushup(root);
    }
}
/********************************* Segment Tree - st *********************************/

int main()
{
    int kase=;
    while(scanf("%d",&n) && n!=)
    {
        x.clear();
        for(int i=;i<=n;i++)
        {
            double x1,x2,y1,y2;
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);

            Segment &s1=segment[*i-];
            Segment &s2=segment[*i];
            s1.l=s2.l=x1;
            s1.r=s2.r=x2;
            s1.h=y1;
            s2.h=y2;
            s1.flag=;
            s2.flag=-;

            x.push_back(x1);
            x.push_back(x2);
        }

        sort(segment+,segment+*n+,cmp);

        //横坐标去重离散化
        sort(x.begin(),x.end());
        x.erase(unique(x.begin(),x.end()),x.end());

        build(,,x.size());
        double ans=;
        for(int i=;i<=*n;i++)
        {
            int l=getID(segment[i].l);
            int r=getID(segment[i].r);
            update(,l,r-,segment[i].flag);
            ans+=node[].len*(segment[i+].h-segment[i].h);
        }
        printf("Test case #%d\n",++kase);
        printf("Total explored area: %.2f\n\n",ans);
    }
}