python数据结构之树（二分查找树）

本篇学习笔记记录二叉查找树的定义以及用python实现数据结构增、删、查的操作。

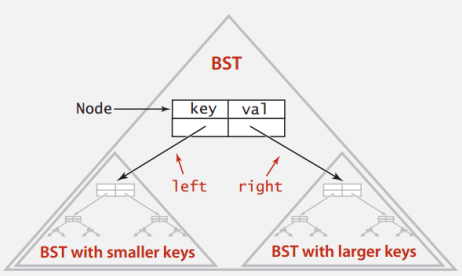
二叉查找树（Binary Search Tree）

简称BST，又叫二叉排序树（Binary Sort Tree），是对称顺序的二叉树，支持多种动态集合操作。

二叉树也是：

• 空
• 两个不相交的二叉树（左和右）

对称顺序

• 每个节点都有一个密钥，每个节点的密钥都是
• 大于其左侧子树中的所有密钥
• 小于其右侧子树中的所有密钥

BST 用Python表示

BST是对根节点的引用

节点由四个字段组成

• 一个 Key 和 一个 Value
• 对左子树(较小的密钥)和右子树(较大的密钥)的引用

class Node(object):
    __slots__ = '_item' , '_lchild' , '_rchild'

    def __init__ (self, item, lchild=None, rchild=None):
        self._item = item
        self._lchild = lchild
        self._rchild = rchild

BST操作方法

• BST 搜索
• BST 插入
• BST获取最小值与最大值
• BST 删除

BST 搜索

• 获取：返回给定键对应的值;如果没有这样的键，则返回null
• 成本：比较的数量等于1 +节点的深度

# Get树元素的方法
    def get(self, key):
        return self.__get(self._root, key);

    def __get(self, node, key): # helper
        if (node is None):
            return None
        if (key == node._item):
            return node._item
        if (key < node._item):
            return self.__get(node._lchild, key)
        else:
            return self.__get(node._rchild, key)

BST 插入

添加：将关联值与关键字关联

搜索密钥，然后搜索两个案例

• 键入树⇒重置值
• 密钥不在树中⇒添加新节点

成本：比较的数量等于1 +节点的深度

# add元素的方法
    def add(self, value):
        self._root = self.__add(self._root, value)

    def __add(self, node, value): # return node ,helper
        if (node is None):
            return Node(value)
        if (value == node._item):
            pass
        else:
            if (value < node._item):
                node._lchild = self.__add(node._lchild, value)
            else:
                node._rchild = self.__add(node._rchild, value)
        return node 

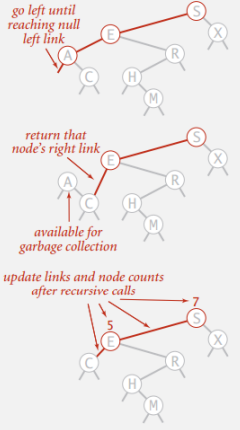
BST 删除

最复杂的二叉搜索树操作

我们必须确保当我们移除一个元素时,我们维护二叉 搜索树属性

删除最小密钥

• 向左移动直到找到带有空左链接的节点
• 用正确的链接替换该节点
• 更新子树计数

# remove树元素的方法
    def remove(self, key):
        self._root = self.__remove(self._root, key)

    def __remove(self, node, key):  # helper
        if node is None:
            return None
        if (key < node._item):
            node._lchild = self.__remove(node._lchild, key)
        elif (key > node._item):
            node._rchild = self.__remove(node._rchild, key)
        else:
            if (node._lchild is None):
                node = node._rchild
            # if rchild is None,  node = None; case 1: no child
            # if rchild is not None, node = node._rchild; case 2: one child
            elif (node._rchild is None):
                node = node._lchild
            else:
                node._item = self.__get_max(node._lchild)
                node._lchild = self.__remove(node._lchild, node._item)

        return node

BST获取最小值与最大值

# get max 元素的方法
    def get_max(self):
        return self.__get_max(self._root)

    def __get_max(self, node): # helper
        if (node is None):
            return None
        while (node._rchild is not None):
            node = node._rchild
        return node._item