DS 红黑树详解

　　　通过上篇博客知道,二叉搜索树的局限在于不能完成自平衡,从而导致不能一直保持高性能。

　　　AVL树则定义了平衡因子绝对值不能大于1,使二叉搜索树达到了严格的高度平衡。

　　　

　　　还有一种能自我调整的二叉搜索树,

　　　红黑树 : 通过标记节点的颜色(红/黑),使其拥有自平衡的二叉搜索树。

　　　　

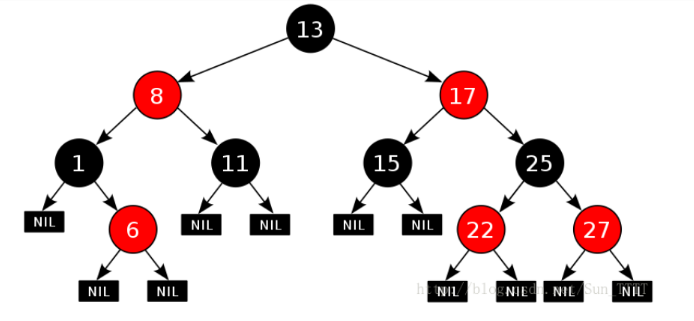
　　　红黑树性质 :

• 性质1：每个节点要么是黑色，要么是红色。
• 性质2：根节点是黑色。
• 性质3：每个叶子节点（NIL）是黑色。
• 性质4：每个红色结点的两个子结点一定都是黑色。
• 性质5：所有路径都包含数量相同的黑结点

　　　　这些约束强制了红黑树的关键性质: 红黑树没有一条路径会比其他路径的两倍长(同一起点)。所以这个树大致上是平衡的,不会像二叉搜索树出现极端情况。

　　　　是性质4和5导致路径上确保了这个结果。最短的路径只有黑色节点，最长路径有交替的红色和黑色节点。因为所有的路径黑色节点数量相同，所以没有路径能多于任何其他路径的两倍长。

　　　　

　　  红黑树节点定义:

enum Colour
 {
   RED,
   BLACK,
 };

 template<class K,class V>
 class RBtreeNode
 {
     RBtree<K,V>* _left;
     RBtree<K,V>* _right;
     RBtree<K,V>* _parent;

     pair<K,V> _kv;
     Colour   _col;
 };

 template<class K,class V>
 class RBTree
 {
     typedef RBtreeNode<K,V> Node;
     public:
         bool Insert(const pair<K,V>& kv);
     private:
         Node* _root = nullptr;
 }

　　　红黑树的插入:

　　　　　　在结点插入后,需要遵循红黑树性质

　　　　　　新结点默认是红色,所以需要判断红黑树的性质是否遭到破坏(插入节点与父亲节点都为红色,违反性质4)

　　　　　　有以下三种情况:

　　　　　　1.u为红   --->   p,u-->黑  g-->红    cur=g,向上调整

　　　　　　

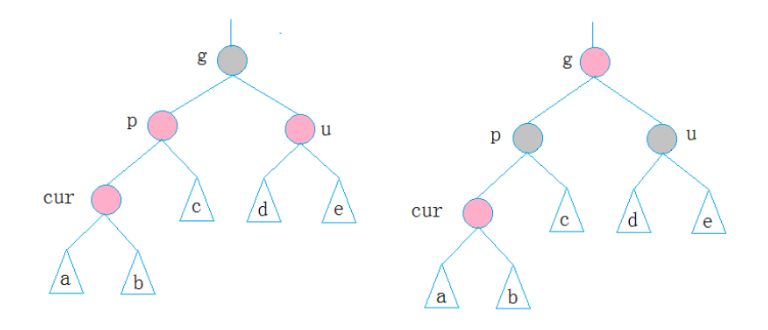
　　　　　　2.cur和p在g的同一边,u不存在/为黑 --- cur,p在g左---  左左 : g右旋, g--->红, p-->黑   

                                                                                     cur,p在g右 --- 右右 : g左旋, g--->红,p--->黑

                             

　　　　3.cur和p不在g的同一边,u不存在/为黑  --- p在g左,cur在p右--- 左右: p左旋

              　　　　　　　　　　　　　　　　　　  p在g右,cur在p左--- 右左: p右旋

　　　　　　　　　　　　　　　　　　             --->变成情况2处理

　　　　      

　　　　　　插入结点代码:

bool Insert(const pair<K,V> _kv)
{
     //插入结点
    if(root == nullptr)
    {
        root=new Node(kv);
        root->_col = BLACK;
        return true;
    }
    Node* parent = nullptr;
    Node* cur = root;
    while(cur)
    {
        if(cur->kv.first < kv.first)

        else if(cur->kv.first > kv.first)

        else
            return false;
    }
    cur = new Node(kv);
    cur->_col = RED;

    //父节点连接插入的结点
    if(parent->kv.first < kv.first)
    {
        parent->_right = cur;
        cur->_parent = parent;
    }
    else
    {
        ...
    }

    //颜色调整
    //红黑树遭到破坏: 红红相连
    while(parent && parent->_col==RED)
    {
        Node* g = parent->_parent;
        //叔叔在右边
        if(parent == g->_left)
        {
            Node* u = g->_right;
            //叔叔为红,变色调整
            if(u && u->_col==RED)
            {
                parent->_col = BLACK;
                u->_col = BLACK;
                g->_col = RED;

                cur = g;
                parent = cur->_parent;
            }
            //叔叔非红,旋转调整
            else
            {
                 //父亲和孩子没有对齐,左旋变齐
                 if(cur == parent->_right)
                  {
                    RotateL(parent);
                    swap(parent,cur);
                  }
                  //对齐,右旋并调色,完成调整
                  RotateR(g);
                  parent->_col = BLACK;
                  g->_col = RED;

                  break;
            }//end of  叔非红处理
        }
        //叔叔在左边
        else
        {
            //....
        }

    }//end of 红红相连

        //按规定将其根置为黑 : 防止根为cur情况
        _root->_col = BLACK;
        return true;
}

　　　　

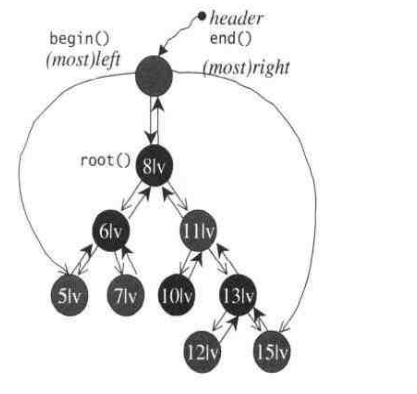
　　　  STL标准的红黑树是这样的, 根的父亲不是nullptr而是header,使红黑树构成了闭环.

　　　　header->_left = rbtree.begin(), header->_right = rbtree.end(), header->_parent = root.

　　　　利用性质验证红黑树代码:

//判断是否为红黑树
bool isRBTree()
{
    pNode root = _header->_parent;

    if(root == nullptr) return true;
    //1.根是否黑色
    if(root->_color == RED)
    {
        cout<<"根节点必须是黑色!"<<endl;
        return false;
    }
    //2.每条路径黑色个数相同?
    //可以任意遍历一条(最右)路径获取黑色节点数量
    pNode cur = root;
    int black_count = 0;
    while(cur)
    {
        if(cur->_color == BLACK)
            ++black_count;
        cur = cur->_right;
    }
    int k = 0;
    return _isRBTree(root,k,black_count); 

}

//看每一条路径是否和基准值相同
bool _isRBTree(pNode root,int curCount,int count)
{
    //终止条件: 一条路径走完
    if(root==nullptr){
        if(curCount != count)
        {
            cout<<"每个路径黑色节点个数不同"<<endl;
            return false;
        }
        return true;
    }

    if(root->_color == BLACK)
        ++curCount;

    //3.没有红色连续的?
    pNode parent = root->_parent;
    if(parent && parent->_color == RED && root->_color == RED)
    {
        cout<<"有红色连续的节点"<<endl;
        return fasle;
    }

    return _isRBTree(root->_left,curCount,count)
    && _isRBTree(root->_right,curCount,count);
}