[BJOI2019]勘破神机（第一类斯特林数，斐波那契数列）

真的是好题，只不过强行多合一有点过分了……

题目大意：

$T$ 组数据。每个测试点中 $m$ 相同。

对于每组数据，给定 $l,r,k$，请求出 $\dfrac{1}{r-l+1}\sum\limits_{n=l}^r\dbinom{f(n,m)}{k}\bmod 998244353$。

其中 $f(n,m)$ 表示用 $1\times 2$ 的骨牌（可以变成 $2\times 1$）填满 $n\times m$ 的网格的方案数。

$1\le T\le 5,1\le l\le r\le 10^{18},1\le k\le 501,2\le m\le 3$。保证 $r-l+1$ 不是 $998244353$ 的倍数。

---

$2\le m\le 3$，明显二合一了。（其实后面会发现不止二合一）

先看 $m=2$。众所周知 $f(n,2)=fib_{n+1}$。然后就变成这题了。注意 $\sqrt{5}$ 在模 $998244353$ 下也没有意义，还是要扩系。

接下来看 $m=3$。

首先肯定 $n$ 是偶数的时候 $f(n,3)$ 才不为 $0$，那么设 $g_n=f(2n,3)$，然后要求就是 $\sum\limits_{n=\lceil\frac{l}{2}\rceil}^{\lfloor\frac{r}{2}\rfloor}g_n$。（为方便下文假设求 $l$ 到 $r$ 的和）

（从题解偷张图，%%%vixbob）

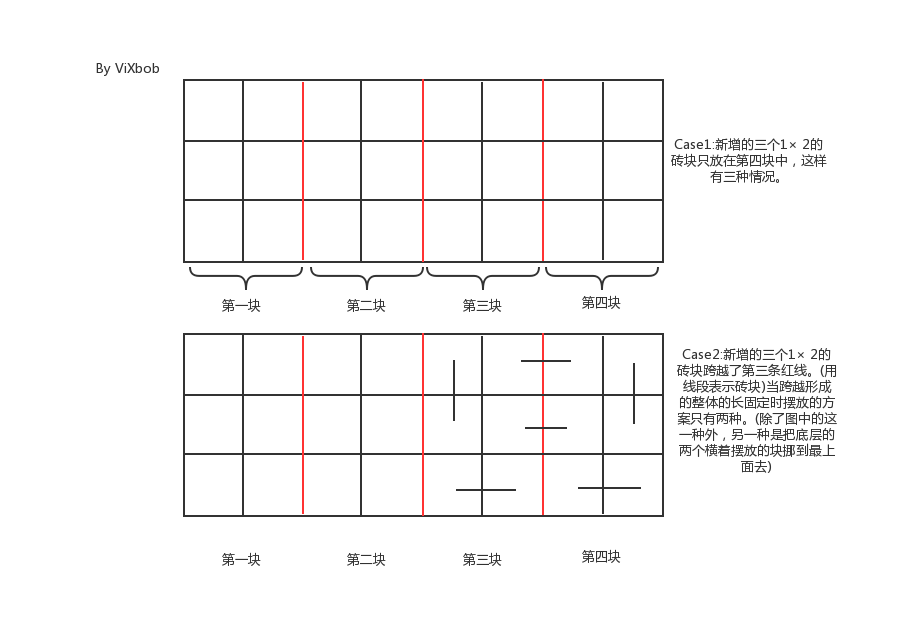
说得应该很清楚了。那么 $g_n=3g_{n-1}+2\sum\limits_{i=0}^{n-2}g_i$。

那么 $g_{n+1}-g_n=3g_n-g_{n-1}$，得递推公式 $g_n=4g_{n-1}-g_{n-2}$。初始 $g_0=1,g_1=3$。

用特征方程解出通项公式：

$$g_n=\dfrac{3+\sqrt{3}}{6}(2+\sqrt{3})^n+\dfrac{3-\sqrt{3}}{6}(2-\sqrt{3})^n$$

然后就一样了。

时间复杂度 $O(Tk^2\log r)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=,mod=,inv2=,inv5=,inv6=;
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline ll read(){
    char ch=getchar();ll x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int t,m,k,fac[maxn],invfac[maxn],S[maxn][maxn],C[maxn][maxn];
ll l,r;
inline int add(int x,int y){return x+y<mod?x+y:x+y-mod;}
inline int sub(int x,int y){return x<y?x-y+mod:x-y;}
inline int mul(int x,int y){return 1ll*x*y%mod;}
inline int qpow(int a,ll b){
    int ans=;
    for(;b;b>>=,a=mul(a,a)) if(b&) ans=mul(ans,a);
    return ans;
}
template<int T>
struct comp{
    int x,y;
    comp(const int xx=,const int yy=):x(xx),y(yy){}
    inline comp operator+(const comp &c)const{return comp(add(x,c.x),add(y,c.y));}
    inline comp operator-(const comp &c)const{return comp(sub(x,c.x),sub(y,c.y));}
    inline comp operator*(const comp &c)const{return comp(add(mul(x,c.x),mul(T,mul(y,c.y))),add(mul(x,c.y),mul(y,c.x)));}
    inline comp inv()const{
        comp ans(x,y?mod-y:);
        int dn=qpow(sub(mul(x,x),mul(T,mul(y,y))),mod-);
        return ans*dn;
    }
    inline comp operator/(const comp &c)const{return *this*c.inv();}
    inline bool operator==(const comp &c)const{return x==c.x && y==c.y;}
};
comp<> a2(,inv5),b2(,mod-inv5),x2(inv2,inv2),y2(inv2,mod-inv2);
comp<> a3(inv2,inv6),b3(inv2,mod-inv6),x3(,),y3(,mod-);
template<int T>
inline comp<T> cqpow(comp<T> a,ll b){
    comp<T> ans(,);
    for(;b;b>>=,a=a*a) if(b&) ans=ans*a;
    return ans;
}
template<int T>
comp<T> calc(comp<T> x,ll l,ll r){
    if(x==) return (r-l+)%mod;
    return (cqpow(x,r+)-cqpow(x,l))/(x-);
}
int main(){
    FOR(i,,) C[i][]=C[i][i]=;
    FOR(i,,) FOR(j,,i-) C[i][j]=add(C[i-][j],C[i-][j-]);
    S[][]=;
    FOR(i,,) FOR(j,,i) S[i][j]=add(mul(i-,S[i-][j]),S[i-][j-]);
    fac[]=;
    FOR(i,,) fac[i]=mul(fac[i-],i);
    invfac[]=qpow(fac[],mod-);
    ROF(i,,) invfac[i]=mul(invfac[i+],i+);
    t=read();m=read();
    while(t--){
        l=read();r=read();k=read();
        if(m==){
            int ans=;
            FOR(i,,k){
                int s=;
                FOR(j,,i){
                    comp<> tmp1=cqpow(a2,j)*cqpow(b2,i-j),tmp2=cqpow(x2,j)*cqpow(y2,i-j);
                    s=add(s,mul(C[i][j],(tmp1*calc(tmp2,l+,r+)).x));
                }
                s=mul(s,S[k][i]);
                if((k-i)&) ans=sub(ans,s);
                else ans=add(ans,s);
            }
            printf("%d\n",mul(mul(ans,invfac[k]),qpow((r-l+)%mod,mod-)));
        }
        else{
            ll lll=(l+)>>,rrr=r>>;
            if(lll>rrr){puts("");continue;}
            int ans=;
            FOR(i,,k){
                int s=;
                FOR(j,,i){
                    comp<> tmp1=cqpow(a3,j)*cqpow(b3,i-j),tmp2=cqpow(x3,j)*cqpow(y3,i-j);
                    s=add(s,mul(C[i][j],(tmp1*calc(tmp2,lll,rrr)).x));
                }
                s=mul(s,S[k][i]);
                if((k-i)&) ans=sub(ans,s);
                else ans=add(ans,s);
            }
            printf("%d\n",mul(mul(ans,invfac[k]),qpow((r-l+)%mod,mod-)));
        }
    }
}