11.04Test

11.04Test

查看请点个赞

转载请注明出处(_不然)

题目	描述	做法
\(BSOJ5143\)	要求给\(M\)个通道染色，使得同色通道不能相交	转为矛盾模型，\(2-sat\)or二分图染色解决
\(BSOJ5145\)	多次加边，维护两点所在点双联通分量大小	\begin{cases}在线:LCT+并查集\离线:直接用并查集来"缩点"\end{cases}
\(BSOJ4932\)	用\(m\)色染\(n\)格子:求染出结果方案数	以匹配数为状态设计\(dp\)再改设状态中点为色块

\(\text{Day1}\)

\(T1\)

n个天使排成一条直线，某些天使之间需要互相联系，他们之间的通讯可以通过黑白两种通道中的一种；所有通道必须在直线同侧（另一侧是地面）；为了保证通讯效率，同种颜色的所有通道之间不能相交。请计算能否建立这种通讯方案。

转问题为矛盾模型:相交的两个区间颜色必须不同

因此用\(2-sat\)和二分图染色均可

注意图可以不连通

\(T2\)

在遥远的S星系中一共有N个星球，编号为1…N。其中的一些星球决定组成联盟，以方便相互间的交流。

　　但是，组成联盟的首要条件就是交通条件。初始时，在这N个星球间有M条太空隧道。每条太空隧道连接两个星球，使得它们能够相互到达。若两个星球属于同一个联盟，则必须存在一条环形线路经过这两个星球，即两个星球间存在两条没有公共隧道的路径。

　　为了壮大联盟的队伍，这些星球将建设P条新的太空隧道。这P条新隧道将按顺序依次建成。一条新轨道建成后，可能会使一些星球属于同一个联盟。你的任务是计算出，在一条新隧道建设完毕后，判断这条新轨道连接的两个星球是否属于同一个联盟，如果属于同一个联盟就计算出这个联盟中有多少个星球。

这里着重讲离线

首先什么时候输出\(No\)

是在询问中一条边合并两个不连通集合时

因此我们考虑一次把所有边加进去，当他可以合并两个集合时才真加

那么最后被加进去的询问边就是这样的合并两个不连通集合的边

因为在它之前没有边做到这一点

然后一条边联通现在点双联通分量形成的树上路径

然后把这条路径上的点缩成一个点双联通分量

这个可以用并查集实现

inline void Merge(re int x,re int y){
	x=getf(x);y=getf(y);
	while(x!=y){
		if(dep[x]<dep[y])swap(x,y);
		size[getf(rt[x])]+=size[x];x=fa[x]=fa[rt[x]];//向上合并
	}
}

\(T3\)(JZOJ6303)

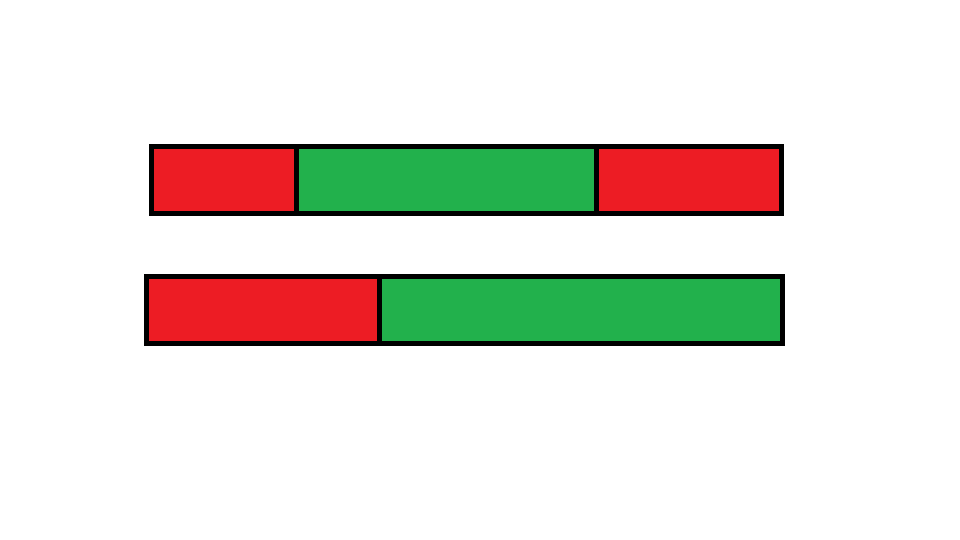
考虑颜色按顺序覆盖是什么意思

那就是一种颜色可以连着出现一段，中间包住一些颜色，然后后面出现一段

但注意，如果\(A\)颜色第一次出现的位置比\(B\)颜色的早，那么\(A\)颜色最后一次出现的位置比\(B\)颜色的晚(类似一个颜色栈)

因此我们在\(dp\)设计中加入一维\(k\)表示栈中还剩\(k\)中颜色或者还剩\(k\)中元素可以延续（注意一点:只要有颜色这个值就$\ge$1）

设\(\displaystyle{dp_{i,j,k}}\)表示有\(i\)个点,\(j\)种颜色曾进过栈,栈中还剩\(k\)中颜色

则\(dp_{i,j,k}\)可以由以下这些状态转移来

\[\begin{cases}dp_{i-1,j,k}&表示扩展一格最后的那种颜色(不结束)\\dp_{i-1,j,k+1}&表示用一个栈内元素(不一定相邻)来结尾这个颜色(出栈)\\dp_{i-1,j-1,k-1}&表示新开一个颜色,并且入栈(以后继续扩展)\\dp_{i-1,j-1,k}&表示新开一个颜色，不入栈(只用这一次)\end{cases}
\]

结合上元素选取的方案

自己推式子!!!

\(dp_{i,j,k}=dp_{i-1,j,k}+dp_{i-1,j,k+1}+(m-j+1)\times(dp_{i-1,j-1,k-1}+dp_{i-1,j-1,k})\)

考虑瓶颈在于第一句话\(dp_{i,j,k}=dp_{i-1,j,k}\)继承连续一段的信息，而其他均为新开或结束一段

复杂度为\(O(nm^2)\)

因此段和点实际上是等价

因此不如改状态为设\(\displaystyle{dp_{i,j,k}}\)表示有\(i\)个段(连续颜色),\(j\)种颜色曾进过栈,栈中还剩\(k\)中颜色

那么因为段数\(\le 2m\)

复杂度为\(O(m^3)\)

\(dp_{i,j,k}=dp_{i-1,j,k+1}+(m-j+1)\times(dp_{i-1,j-1,k-1}+dp_{i-1,j-1,k})\)

不放代码了，因为初始条件总该自己推把