决策树（ID3、C4.5、CART算法numpy实现）
什么是决策树？
决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。
其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。
使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。
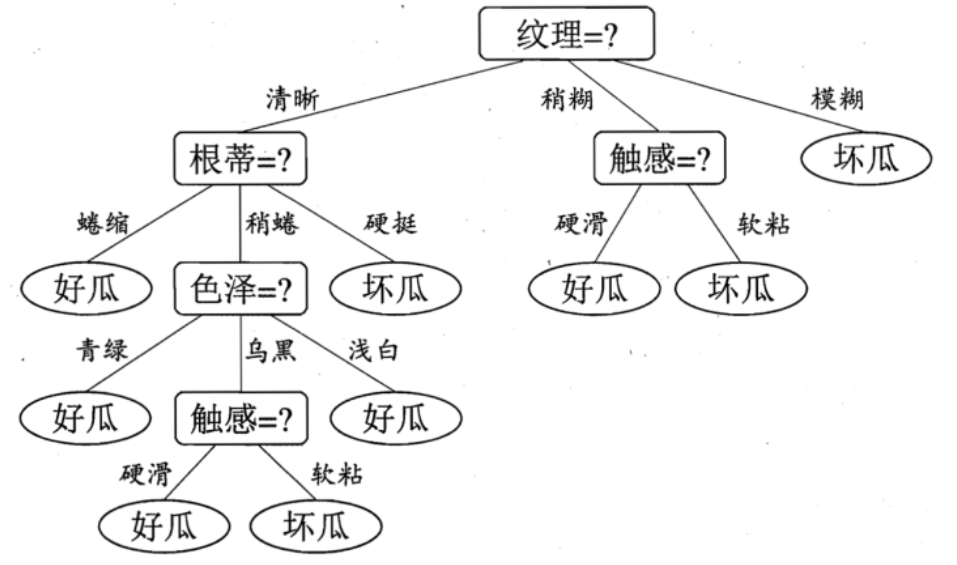
（图片来源）
如何建树？
建树的关键在于特征选择，我们应当选择怎么样的特征作为我们的判断条件。
大致有三种算法：
1、ID3算法：基于信息增益准则选择特征
2、C4.5算法：基于信息增益比来选择特征
3、CART算法：基于基尼指数来选择特征
1、ID3算法：
如何计算信息增益：
K是分类值y的种类，| |表示样本数量，n表示特征A所有可能的取值（这句话的意思是枚举所有在训练集出现过的值，即使在某层中该取值的样本数为0）。
例如：（图片来源）
ID3算法流程如下：
代码实现：
使用信息增益进行特征选择的缺点：偏向于选择取值较多的特征，可以理解为倾向划分更多的子树。
import numpy as np
from math import log2 as log
class TreeNode(object):
def __init__(self,X,Y,S):
self.label = None
self.divide_dim = None
self.X = X
self.Y = Y
self.children = {}
self.is_leaf = True
self.source =S #为了display函数
self.id = None #节点ID,确保唯一
self.child_ids =[] class DecisionTree(object):
def __init__(self,X,Y,function='ID3'):
self.X = X
self.Y = Y
self.F = function
self.num_features = len(X[0]) #特征数
self.feature_map = {} #特征映射为int值
self.maps = {} #每个特征中对应的值的映射，例如第二个特征，有一个叫‘是’，那么maps[1]['是']=0/1
self.label_map = {} #y 标签映射为数值
self.root = None
self.epsilon = 0
self.inv_maps={}
self.ID = 1 def train(self):
# train函数主要是处理数据，把所有特征转化为数值型，方便使用numpy处理
X = self.X
Y = self.Y
# X row = Y row +1
# 默认X的第一行为特征描述
features = X[0]
xx = np.zeros([len(X),self.num_features],dtype=int)
yy = np.zeros(len(Y),dtype=int)
for feature,j in zip(features,range(self.num_features)):
self.feature_map[feature] = j
self.maps[j] ={}
self.inv_maps[j]={}
for i in range(1,len(X)):
k = X[i][j]
if k in self.maps[j].keys():
xx[i][j] = self.maps[j][k]
else:
self.maps[j][k] = len(self.maps[j])
xx[i][j] =self.maps[j][k]
self.inv_maps[j][xx[i][j]]=k for i in range(len(Y)):
k= Y[i]
if k in self.label_map.keys():
yy[i] = self.label_map[k]
else:
self.label_map[k] = len(self.label_map)
yy[i] = self.label_map[k]
xx = xx[1:]
X = X[1:]
# xx , yy all int
self.root = TreeNode(xx,yy,xx)
self.root.id = self.ID
self.ID = self.ID+1
print(self.root.X)
print(self.root.Y)
self.build_tree(self.root) def get_information_gain(self,X,Y,dim,idx):
# dim 表示特征索引
nums = X.shape[0]
cnt_class = len(self.label_map)
cnt_x = len(self.maps[dim])
xx = X[:,dim]
yy = Y
hd =0
for v in range(cnt_class):
nums_v = np.where(yy==v,1,0).sum()
if nums_v >0 :
hd = hd - nums_v*log(nums_v/nums)/nums
hda = 0
for i in range(cnt_x):
di = np.where(xx==i,1,0).sum()
if di>0:
tmpy=yy[np.where(xx==i,True,False)]
for k in range(cnt_class):
dik = np.where(tmpy== k,1,0).sum()
if dik >0:
hda = hda - (di/nums)*(dik/di)*log(dik/di)
# 显示当前节点计算的指定维度的信息增益
inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
print('当前节点序号: ', idx, ' 特征: ', inv_feature_map[dim])
print('information gain', hd - hda)
return hd-hda def build_tree(self,root):
if self.check_all_y(root.Y): #所有实例属于同一类
root.is_leaf=True
root.label = root.Y[0]
elif self.check_X_null(root.X): #特征为空，无法进一步选择划分,标记为-1的列即表示已经使用过
root.is_leaf=True
root.label = self.get_max_y(root.Y)
else:
epsilon = self.epsilon #epsilon
mx_dim = -1 #选取信息增益最大的作为特征维度
for dim in self.maps.keys():
if root.X[0,dim] != -1:
gda = self.get_information_gain(root.X,root.Y,dim,root.id)
if gda > epsilon:
epsilon =gda
mx_dim=dim
if mx_dim == -1:
root.is_leaf = True
root.label = self.get_max_y(root.Y)
else:
root.divide_dim = mx_dim
root.is_leaf = False
root.label = self.get_max_y(root.Y)
xx = root.X
yy = root.Y
for i in range(len(self.maps[mx_dim])):
tmpx = xx[np.where(xx[:,mx_dim]==i,True,False)]
tmps = root.source[np.where(xx[:, mx_dim] == i, True, False)]
tmpx[:,mx_dim] =-1 #将使用过的特征标记为-1
tmpy = yy[np.where(xx[:,mx_dim]==i,True,False)]
child = TreeNode(tmpx,tmpy,tmps)
child.id = self.ID
self.ID = self.ID + 1
root.child_ids.append(child.id)
root.children[i] = child
if tmpx.shape[0] == 0: #如果为空集，子节点的类别和当前节点保持一致
child.is_leaf=True
child.label = root.label
else:
child.is_leaf=False
child.X = tmpx
child.Y = tmpy
self.build_tree(child)
pass def check_all_y(self,Y):
yy = Y - Y[0]
if np.where(yy==0,0,1).sum()==0:
return True
else:
return False
def check_X_null(self,X):
if np.where(X==-1,0,1).sum()==0:
return True
else:
return False
def get_max_y(self,Y): #选取最大类别
mx = 0
for k in range(len(self.label_map)):
dk = np.where(Y == k, 1, 0).sum()
if mx < dk:
label = k
mx = dk
return label def display(self):
mp = dict(zip(self.label_map.values(),self.label_map.keys()))
inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
q= []
q.append(self.root)
while len(q)>0:
root = q[0]
c= q.pop(0)
if root.is_leaf:
print(root.id, mp[root.label],' is leaf')
ss = []
for idx in range(root.source.shape[0]):
s = root.source[idx]
sen = []
for i in range(s.shape[0]):
sen.append(self.inv_maps[i][s[i]])
ss.append(sen)
print(ss)
else :
print(root.id, 'divide dim ', inv_feature_map[root.divide_dim], '*' * 20)
print(root.child_ids)
ss = []
for idx in range(root.source.shape[0]):
s = root.source[idx]
sen = []
for i in range(s.shape[0]):
sen.append(self.inv_maps[i][s[i]])
ss.append(sen)
print(ss)
for i in range(len(self.maps[root.divide_dim])):
q.append(root.children[i])
pass def _predict(self,root,x): dim = root.divide_dim
if root.is_leaf:
return root.label if x[dim] not in self.maps[dim].keys():
return self.root.label return self._predict(root.children[self.maps[dim][x[dim]]], x) def predict(self,x):
pred_label = self._predict(self.root,x)
for k,v in self.label_map.items():
if v==pred_label:
return k # X = [[1,2,3,4,5,6],['青年','否','一般'],['青年','否','好'],['青年','是','好'],['青年','是','一般'],
# ['青年','否','一般'],['中年','否','一般'],['中年','否','一般'],
# ['中年','是','好'],['中年','否','一般']]
# y = ['否','否','是','是','否','否','否','是','是'] X = [['色泽','根蒂','敲声','纹理','脐部','触感'],
['青绿','蜷缩','沉闷','清晰','凹陷','硬滑'],
['浅白','蜷缩','浊响','清晰','凹陷','硬滑'],
['乌黑','稍蜷','浊响','清晰','稍凹','硬滑'],
['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑'],
['浅白','硬挺','清脆','模糊','平坦','硬滑'],
['浅白','蜷缩','浊响','模糊','平坦','软粘'],
['青绿','稍蜷','浊响','稍糊','凹陷','硬滑']]
y = ['是','是','是','否','否','否','否']
dt = DecisionTree(X,y)
dt.train()
dt.display()
# 新增加了决策树的预测函数
print(dt.predict(['青绿','稍蜷','浊响','稍糊','非常平坦','硬滑']))
最新版代码,增加了决策树的预测函数
1 import numpy as np
2 from math import log2 as log
3 class TreeNode(object):
4 def __init__(self,X,Y,S):
5 self.label = None
6 self.divide_dim = None
7 self.X = X
8 self.Y = Y
9 self.children = {}
10 self.is_leaf = True
11 self.source =S #为了display函数
12 self.id = None #节点ID,确保唯一
13 self.child_ids =[]
14
15 class DecisionTree(object):
16 def __init__(self,X,Y,function='ID3'):
17 self.X = X
18 self.Y = Y
19 self.F = function
20 self.num_features = len(X[0]) #特征数
21 self.feature_map = {} #特征映射为int值
22 self.maps = {} #每个特征中对应的值的映射，例如第二个特征，有一个叫‘是’，那么maps[1]['是']=0/1
23 self.label_map = {} #y 标签映射为数值
24 self.root = None
25 self.epsilon = 0
26 self.inv_maps={}
27 self.ID = 1
28
29 def train(self):
30 # train函数主要是处理数据，把所有特征转化为数值型，方便使用numpy处理
31 X = self.X
32 Y = self.Y
33 # X row = Y row +1
34 # 默认X的第一行为特征描述
35 features = X[0]
36 xx = np.zeros([len(X),self.num_features],dtype=int)
37 yy = np.zeros(len(Y),dtype=int)
38 for feature,j in zip(features,range(self.num_features)):
39 self.feature_map[feature] = j
40 self.maps[j] ={}
41 self.inv_maps[j]={}
42 for i in range(1,len(X)):
43 k = X[i][j]
44 if k in self.maps[j].keys():
45 xx[i][j] = self.maps[j][k]
46 else:
47 self.maps[j][k] = len(self.maps[j])
48 xx[i][j] =self.maps[j][k]
49 self.inv_maps[j][xx[i][j]]=k
50
51 for i in range(len(Y)):
52 k= Y[i]
53 if k in self.label_map.keys():
54 yy[i] = self.label_map[k]
55 else:
56 self.label_map[k] = len(self.label_map)
57 yy[i] = self.label_map[k]
58 xx = xx[1:]
59 X = X[1:]
60 # xx , yy all int
61 self.root = TreeNode(xx,yy,xx)
62 self.root.id = self.ID
63 self.ID = self.ID+1
64 print(self.root.X)
65 print(self.root.Y)
66 self.build_tree(self.root)
67
68 def get_information_gain(self,X,Y,dim,idx):
69 # dim 表示特征索引
70 nums = X.shape[0]
71 cnt_class = len(self.label_map)
72 cnt_x = len(self.maps[dim])
73 xx = X[:,dim]
74 yy = Y
75 hd =0
76 for v in range(cnt_class):
77 nums_v = np.where(yy==v,1,0).sum()
78 if nums_v >0 :
79 hd = hd - nums_v*log(nums_v/nums)/nums
80 hda = 0
81 for i in range(cnt_x):
82 di = np.where(xx==i,1,0).sum()
83 if di>0:
84 tmpy=yy[np.where(xx==i,True,False)]
85 for k in range(cnt_class):
86 dik = np.where(tmpy== k,1,0).sum()
87 if dik >0:
88 hda = hda - (di/nums)*(dik/di)*log(dik/di)
89 # 显示当前节点计算的指定维度的信息增益
90 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
91 print('当前节点序号: ', idx, ' 特征: ', inv_feature_map[dim])
92 print('information gain', hd - hda)
93 return hd-hda
94
95 def build_tree(self,root):
96 if self.check_all_y(root.Y): #所有实例属于同一类
97 root.is_leaf=True
98 root.label = root.Y[0]
99 elif self.check_X_null(root.X): #特征为空，无法进一步选择划分,标记为-1的列即表示已经使用过
100 root.is_leaf=True
101 root.label = self.get_max_y(root.Y)
102 else:
103 epsilon = self.epsilon #epsilon
104 mx_dim = -1 #选取信息增益最大的作为特征维度
105 for dim in self.maps.keys():
106 if root.X[0,dim] != -1:
107 gda = self.get_information_gain(root.X,root.Y,dim,root.id)
108 if gda > epsilon:
109 epsilon =gda
110 mx_dim=dim
111 if mx_dim == -1:
112 root.is_leaf = True
113 root.label = self.get_max_y(root.Y)
114 else:
115 root.divide_dim = mx_dim
116 root.is_leaf = False
117 root.label = self.get_max_y(root.Y)
118 xx = root.X
119 yy = root.Y
120 for i in range(len(self.maps[mx_dim])):
121 tmpx = xx[np.where(xx[:,mx_dim]==i,True,False)]
122 tmps = root.source[np.where(xx[:, mx_dim] == i, True, False)]
123 tmpx[:,mx_dim] =-1 #将使用过的特征标记为-1
124 tmpy = yy[np.where(xx[:,mx_dim]==i,True,False)]
125 child = TreeNode(tmpx,tmpy,tmps)
126 child.id = self.ID
127 self.ID = self.ID + 1
128 root.child_ids.append(child.id)
129 root.children[i] = child
130 if tmpx.shape[0] == 0: #如果为空集，子节点的类别和当前节点保持一致
131 child.is_leaf=True
132 child.label = root.label
133 else:
134 child.is_leaf=False
135 child.X = tmpx
136 child.Y = tmpy
137 self.build_tree(child)
138 pass
139 def check_all_y(self,Y):
140 yy = Y - Y[0]
141 if np.where(yy==0,0,1).sum()==0:
142 return True
143 else:
144 return False
145 def check_X_null(self,X):
146 if np.where(X==-1,0,1).sum()==0:
147 return True
148 else:
149 return False
150 def get_max_y(self,Y): #选取最大类别
151 mx = 0
152 for k in range(len(self.label_map)):
153 dk = np.where(Y == k, 1, 0).sum()
154 if mx < dk:
155 label = k
156 mx = dk
157 return label
158
159 def display(self):
160 mp = dict(zip(self.label_map.values(),self.label_map.keys()))
161 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
162 q= []
163 q.append(self.root)
164 while len(q)>0:
165 root = q[0]
166 c= q.pop(0)
167 if root.is_leaf:
168 print(root.id, mp[root.label],' is leaf')
169 ss = []
170 for idx in range(root.source.shape[0]):
171 s = root.source[idx]
172 sen = []
173 for i in range(s.shape[0]):
174 sen.append(self.inv_maps[i][s[i]])
175 ss.append(sen)
176 print(ss)
177 else :
178 print(root.id, 'divide dim ', inv_feature_map[root.divide_dim], '*' * 20)
179 print(root.child_ids)
180 ss = []
181 for idx in range(root.source.shape[0]):
182 s = root.source[idx]
183 sen = []
184 for i in range(s.shape[0]):
185 sen.append(self.inv_maps[i][s[i]])
186 ss.append(sen)
187 print(ss)
188 for i in range(len(self.maps[root.divide_dim])):
189 q.append(root.children[i])
190 pass
191
192
193
194 X = [['色泽','根蒂','敲声','纹理','脐部','触感'],
195 ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑'],
196 ['浅白','蜷缩','浊响','清晰','凹陷','硬滑'],
197 ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑'],
198 ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑'],
199 ['浅白','硬挺','清脆','模糊','平坦','硬滑'],
200 ['浅白','蜷缩','浊响','模糊','平坦','软粘'],
201 ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑']]
202 y = ['是','是','是','否','否','否','否']
203 dt = DecisionTree(X,y)
204 dt.train()
205 dt.display()
2、C4.5算法：
按信息增益比来选择特征：
缺点：偏向于选择取值数目较少的特征，因为HA(D)其实可以认为把特征A的取值看做一个随机变量。要让信息增益比尽可能大，会倾向选择特征取值的不确定度尽可能低的特征。比如特征A只有两个取值，特征B有三种取值，假设取值是均匀分布，那么经过计算HA(D) < HB(D)，说明模型倾向选择不确定度小的特征，假设是取值是均匀分布，那么极有可能是选择取值数目较少的特征。
算法流程：
C4.5 [Quinlan, 1993]使用了一个启发式方法：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取信息增益比最高的。
本人代码实现并没有用启发式的方法。C4.5的代码和ID3差不多。
1 import numpy as np
2 from math import log2 as log
3 class TreeNode(object):
4 def __init__(self,X,Y,S):
5 self.label = None
6 self.divide_dim = None
7 self.X = X
8 self.Y = Y
9 self.children = {}
10 self.is_leaf = True
11 self.source =S #为了display函数
12 self.id = None #节点ID,确保唯一
13 self.child_ids =[]
14
15 class DecisionTree(object):
16 def __init__(self,X,Y,function='C4.5'):
17 self.X = X
18 self.Y = Y
19 self.F = function
20 self.num_features = len(X[0]) #特征数
21 self.feature_map = {} #特征映射为int值
22 self.maps = {} #每个特征中对应的值的映射，例如第二个特征，有一个叫‘是’，那么maps[1]['是']=0/1
23 self.label_map = {} #y 标签映射为数值
24 self.root = None
25 self.epsilon = 0
26 self.inv_maps={}
27 self.ID = 1
28
29 def train(self):
30 # train函数主要是处理数据，把所有特征转化为数值型，方便使用numpy处理
31 X = self.X
32 Y = self.Y
33 # X row = Y row +1
34 # 默认X的第一行为特征描述
35 features = X[0]
36 xx = np.zeros([len(X),self.num_features],dtype=int)
37 yy = np.zeros(len(Y),dtype=int)
38 for feature,j in zip(features,range(self.num_features)):
39 self.feature_map[feature] = j
40 self.maps[j] ={}
41 self.inv_maps[j]={}
42 for i in range(1,len(X)):
43 k = X[i][j]
44 if k in self.maps[j].keys():
45 xx[i][j] = self.maps[j][k]
46 else:
47 self.maps[j][k] = len(self.maps[j])
48 xx[i][j] =self.maps[j][k]
49 self.inv_maps[j][xx[i][j]]=k
50
51 for i in range(len(Y)):
52 k= Y[i]
53 if k in self.label_map.keys():
54 yy[i] = self.label_map[k]
55 else:
56 self.label_map[k] = len(self.label_map)
57 yy[i] = self.label_map[k]
58 xx = xx[1:]
59 X = X[1:]
60 # xx , yy all int
61 self.root = TreeNode(xx,yy,xx)
62 self.root.id = self.ID
63 self.ID = self.ID+1
64 print(self.root.X)
65 print(self.root.Y)
66 self.build_tree(self.root)
67
68 def get_information_gain_rate(self,X,Y,dim,idx):
69 # dim 表示特征索引
70 nums = X.shape[0]
71 cnt_class = len(self.label_map)
72 cnt_x = len(self.maps[dim])
73 xx = X[:,dim]
74 yy = Y
75 hd =0
76 for v in range(cnt_class):
77 nums_v = np.where(yy==v,1,0).sum()
78 if nums_v >0 :
79 hd = hd - nums_v*log(nums_v/nums)/nums
80 hda = 0
81 had = 0
82 for i in range(cnt_x):
83 di = np.where(xx==i,1,0).sum()
84 if di>0:
85 had = had - (di/nums)*log(di/nums)
86 tmpy=yy[np.where(xx==i,True,False)]
87 for k in range(cnt_class):
88 dik = np.where(tmpy== k,1,0).sum()
89 if dik >0:
90 hda = hda - (di/nums)*(dik/di)*log(dik/di)
91 ## 显示计算的指定维度的信息增益和信息增益比
92 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
93 print('当前节点序号: ',idx,' 特征: ',inv_feature_map[dim])
94 print('information gain',hd-hda)
95 if had == 0:
96 print('igr: ',(hd-hda)/1e-9)
97 return (hd-hda)/1e-9
98 else :
99 print('igr: ', (hd - hda) / had)
100 return (hd-hda)/had
101
102 def build_tree(self,root):
103 if self.check_all_y(root.Y): #所有实例属于同一类
104 root.is_leaf=True
105 root.label = root.Y[0]
106 elif self.check_X_null(root.X): #特征为空，无法进一步选择划分,标记为-1的列即表示已经使用过
107 root.is_leaf=True
108 root.label = self.get_max_y(root.Y)
109 else:
110 epsilon = self.epsilon #epsilon
111 mx_dim = -1 #选取信息增益比最大的作为特征维度
112 for dim in self.maps.keys():
113 if root.X[0,dim] != -1:
114 gda = self.get_information_gain_rate(root.X,root.Y,dim,root.id)
115 if gda > epsilon:
116 epsilon =gda
117 mx_dim=dim
118 if mx_dim == -1:
119 root.is_leaf = True
120 root.label = self.get_max_y(root.Y)
121 else:
122 root.divide_dim = mx_dim
123 root.is_leaf = False
124 root.label = self.get_max_y(root.Y)
125 xx = root.X
126 yy = root.Y
127 for i in range(len(self.maps[mx_dim])):
128 tmpx = xx[np.where(xx[:,mx_dim]==i,True,False)]
129 tmps = root.source[np.where(xx[:, mx_dim] == i, True, False)]
130 tmpx[:,mx_dim] =-1 #将使用过的特征标记为-1
131 tmpy = yy[np.where(xx[:,mx_dim]==i,True,False)]
132 child = TreeNode(tmpx,tmpy,tmps)
133 child.id = self.ID
134 self.ID = self.ID + 1
135 root.child_ids.append(child.id)
136 root.children[i] = child
137 if tmpx.shape[0] == 0: #如果为空集，子节点的类别和当前节点保持一致
138 child.is_leaf=True
139 child.label = root.label
140 else:
141 child.is_leaf=False
142 child.X = tmpx
143 child.Y = tmpy
144 self.build_tree(child)
145 pass
146 def check_all_y(self,Y):
147 yy = Y - Y[0]
148 if np.where(yy==0,0,1).sum()==0:
149 return True
150 else:
151 return False
152 def check_X_null(self,X):
153 if np.where(X==-1,0,1).sum()==0:
154 return True
155 else:
156 return False
157 def get_max_y(self,Y): #选取最大类别
158 mx = 0
159 for k in range(len(self.label_map)):
160 dk = np.where(Y == k, 1, 0).sum()
161 if mx < dk:
162 label = k
163 mx = dk
164 return label
165
166 def display(self):
167 mp = dict(zip(self.label_map.values(),self.label_map.keys()))
168 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
169 q= []
170 q.append(self.root)
171 while len(q)>0:
172 root = q[0]
173 c= q.pop(0)
174 if root.is_leaf:
175 print(root.id, mp[root.label],' is leaf')
176 ss = []
177 for idx in range(root.source.shape[0]):
178 s = root.source[idx]
179 sen = []
180 for i in range(s.shape[0]):
181 sen.append(self.inv_maps[i][s[i]])
182 ss.append(sen)
183 print(ss)
184 else :
185 print(root.id,'divide dim ',inv_feature_map[root.divide_dim],'*'*20)
186 print(root.child_ids)
187 ss = []
188 for idx in range(root.source.shape[0]):
189 s = root.source[idx]
190 sen = []
191 for i in range(s.shape[0]):
192 sen.append(self.inv_maps[i][s[i]])
193 ss.append(sen)
194 print(ss)
195 for i in range(len(self.maps[root.divide_dim])):
196 q.append(root.children[i])
197 pass
198
199
200 X = [['色泽','根蒂','敲声','纹理','脐部','触感'],
201 ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑'],
202 ['浅白','蜷缩','浊响','清晰','凹陷','硬滑'],
203 ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑'],
204 ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑'],
205 ['浅白','硬挺','清脆','模糊','平坦','硬滑'],
206 ['浅白','蜷缩','浊响','模糊','平坦','软粘'],
207 ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑']]
208 y = ['是','是','是','否','否','否','否']
209 dt = DecisionTree(X,y)
210 dt.train()
211 dt.display()
3、CART(Classification And Regression Tree)算法：
本文仅做了分类树的实现。
CART算法得到的决策树是一棵二叉树。
特征选择使用的是基尼指数（Gini index）最小化原则。
CART分类树的算法流程：
算法的终止条件是结点中的样本数少于某个阈值，或者样本集的基尼指数小于预定值(样本基本属于同一类)，或者没有更多特征。
本文没有考虑第一个终止特征，使用了和ID3、C4.5一样的终止条件。
关于决策树的剪枝，笔者时间不充裕，有空再补一篇。
代码如下：
1 import numpy as np
2 from math import log2 as log
3 class TreeNode(object):
4 def __init__(self,X,Y,S):
5 self.label = None
6 self.divide_dim = None
7 self.X = X
8 self.Y = Y
9 self.children = {}
10 self.is_leaf = True
11 self.source =S #为了display函数，显示X设为-1的值
12 self.id = None #节点ID,确保唯一
13 self.child_ids =[]
14
15 class DecisionTree(object):
16 def __init__(self,X,Y,function='CART'):
17 self.X = X
18 self.Y = Y
19 self.F = function
20 self.num_features = len(X[0]) #特征数
21 self.feature_map = {} #特征映射为int值
22 self.maps = {} #每个特征中对应的值的映射，例如第二个特征，有一个叫‘是’，那么maps[1]['是']=0/1
23 self.label_map = {} #y 标签映射为数值
24 self.root = None
25 self.inv_maps={}
26 self.ID = 1
27
28 def train(self):
29 # train函数主要是处理数据，把所有特征转化为数值型，方便使用numpy处理
30 X = self.X
31 Y = self.Y
32 # X row = Y row +1
33 # 默认X的第一行为特征描述
34 features = X[0]
35 xx = np.zeros([len(X),self.num_features],dtype=int)
36 yy = np.zeros(len(Y),dtype=int)
37 for feature,j in zip(features,range(self.num_features)):
38 self.feature_map[feature] = j
39 self.maps[j] ={}
40 self.inv_maps[j]={}
41 for i in range(1,len(X)):
42 k = X[i][j]
43 if k in self.maps[j].keys():
44 xx[i][j] = self.maps[j][k]
45 else:
46 self.maps[j][k] = len(self.maps[j])
47 xx[i][j] =self.maps[j][k]
48 self.inv_maps[j][xx[i][j]]=k
49
50 for i in range(len(Y)):
51 k= Y[i]
52 if k in self.label_map.keys():
53 yy[i] = self.label_map[k]
54 else:
55 self.label_map[k] = len(self.label_map)
56 yy[i] = self.label_map[k]
57 xx = xx[1:]
58 # xx , yy all int
59 self.root = TreeNode(xx,yy,xx)
60 self.root.id = self.ID
61 self.ID = self.ID+1
62 print(self.root.X)
63 print(self.root.Y)
64 self.build_tree(self.root)
65
66 def get_mini_Gini_split(self,X,Y,dim,idx):
67 # 获取当前维度最小基尼值的划分值
68 # dim 表示特征索引
69 nums = X.shape[0]
70 cnt_class = len(self.label_map)
71 cnt_x = len(self.maps[dim])
72 xx = X[:,dim]
73 yy = Y
74 split_value = -1
75 mini_gini = 1.1 #需要比最大值大一点
76 for i in range(cnt_x):
77 num_equal= np.where(xx==i,1,0).sum()
78 num_diff = nums - num_equal
79 if num_diff==0 or num_equal ==0:
80 continue
81 equal_y = yy[np.where(xx==i,True,False)]
82 diff_y = yy[np.where(xx==i,False,True)]
83 equal_gini = 1
84 diff_gini = 1
85 for k in range(cnt_class):
86 equal_gini = equal_gini -((np.where(equal_y== k,1,0).sum())/num_equal)**2
87 diff_gini = diff_gini - ((np.where(diff_y==k,1,0).sum())/num_diff)**2
88 gini = num_equal*equal_gini/nums + num_diff*diff_gini/nums
89 if gini < mini_gini:
90 mini_gini=gini
91 split_value = i
92 #########
93 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
94 print('当前节点序号: ', idx, ' 特征: ', inv_feature_map[dim])
95 if split_value==-1: #说明无法找到一个分割点将样本分为两份
96 print('当前特征无法切分')
97 return split_value,mini_gini
98 print(mini_gini,split_value)
99 print('基尼值: ',mini_gini,' 分割值: ',self.inv_maps[dim][split_value])
100
101 return split_value,mini_gini
102
103 def build_tree(self,root):
104 if self.check_all_y(root.Y): #所有实例属于同一类
105 root.is_leaf=True
106 root.label = root.Y[0]
107 elif self.check_X_null(root.X): #特征为空，无法进一步选择划分,标记为-1的列即表示已经使用过
108 root.is_leaf=True
109 root.label = self.get_max_y(root.Y)
110 else:
111 gini = 1.1 #需要比最大值大一点
112 mx_dim = -1
113 split_value = -1
114 for dim in self.maps.keys():
115 if root.X[0,dim] != -1:
116 split, mini_gini = self.get_mini_Gini_split(root.X,root.Y,dim,root.id)
117 #print(mx_dim,split_value,mini_gini)
118 if mini_gini < gini:
119 gini = mini_gini
120 mx_dim = dim
121 split_value = split
122 if mx_dim == -1:
123 root.is_leaf = True
124 root.label = self.get_max_y(root.Y)
125 else:
126 root.divide_dim = mx_dim
127 root.is_leaf = False
128 root.label = self.get_max_y(root.Y)
129 xx = root.X
130 yy = root.Y
131 flag = True #用来选择样本
132 for i in range(2):
133 tmpx = xx[np.where(xx[:,mx_dim]==split_value,flag,not flag)]
134 tmps = root.source[np.where(xx[:, mx_dim] == split_value, flag,not flag)]
135 tmpx[:,mx_dim] =-1 #将使用过的特征标记为-1
136 tmpy = yy[np.where(xx[:,mx_dim]==split_value,flag,not flag)]
137 flag=False #转换一下
138 child = TreeNode(tmpx,tmpy,tmps)
139 child.id = self.ID
140 self.ID = self.ID + 1
141 root.child_ids.append(child.id)
142 root.children[i] = child
143 if tmpx.shape[0] == 0: #如果为空集，子节点的类别和当前节点保持一致
144 child.is_leaf=True
145 child.label = root.label
146 else:
147 child.is_leaf=False
148 child.X = tmpx
149 child.Y = tmpy
150 self.build_tree(child)
151 pass
152 def check_all_y(self,Y):
153 yy = Y - Y[0]
154 if np.where(yy==0,0,1).sum()==0:
155 return True
156 else:
157 return False
158 def check_X_null(self,X):
159 if np.where(X==-1,0,1).sum()==0:
160 return True
161 else:
162 return False
163 def get_max_y(self,Y): #选取最大类别
164 mx = 0
165 for k in range(len(self.label_map)):
166 dk = np.where(Y == k, 1, 0).sum()
167 if mx < dk:
168 label = k
169 mx = dk
170 return label
171
172 def display(self):
173 mp = dict(zip(self.label_map.values(),self.label_map.keys()))
174 inv_feature_map = dict(zip(self.feature_map.values(), self.feature_map.keys()))
175 q= []
176 q.append(self.root)
177 while len(q)>0:
178 root = q[0]
179 c= q.pop(0)
180 if root.is_leaf:
181 print(root.id, mp[root.label],' is leaf')
182 ss = []
183 for idx in range(root.source.shape[0]):
184 s = root.source[idx]
185 sen = []
186 for i in range(s.shape[0]):
187 sen.append(self.inv_maps[i][s[i]])
188 ss.append(sen)
189 print(ss)
190 else :
191 print(root.id,'divide dim ',inv_feature_map[root.divide_dim],'*'*20)
192 print(root.child_ids)
193 ss = []
194 for idx in range(root.source.shape[0]):
195 s = root.source[idx]
196 sen = []
197 for i in range(s.shape[0]):
198 sen.append(self.inv_maps[i][s[i]])
199 ss.append(sen)
200 print(ss)
201 for i in range(len(root.children)):
202 q.append(root.children[i])
203 pass
204
205
206 X = [['色泽','根蒂','敲声','纹理','脐部','触感'],
207 ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑'],
208 ['浅白','蜷缩','浊响','清晰','凹陷','硬滑'],
209 ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑'],
210 ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑'],
211 ['浅白','硬挺','清脆','模糊','平坦','硬滑'],
212 ['浅白','蜷缩','浊响','模糊','平坦','软粘'],
213 ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑']]
214 y = ['是','是','是','否','否','否','否']
215 dt = DecisionTree(X,y)
216 dt.train()
217 dt.display()
参考文献：
1、周志华——《机器学习》
2、李航——《统计学习方法》(第二版)
决策树（ID3、C4.5、CART算法numpy实现）的更多相关文章
- 决策树模型 ID3/C4.5/CART算法比较
决策树模型在监督学习中非常常见,可用于分类(二分类.多分类)和回归.虽然将多棵弱决策树的Bagging.Random Forest.Boosting等tree ensembel 模型更为常见,但是“完 ...
- 决策树(ID3,C4.5,CART)原理以及实现
决策树 决策树是一种基本的分类和回归方法.决策树顾名思义,模型可以表示为树型结构,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布. [图片上传失败...(image ...
- 决策树 ID3 C4.5 CART（未完）
1.决策树 :监督学习 决策树是一种依托决策而建立起来的一种树. 在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某 ...
- 21.决策树(ID3/C4.5/CART)
总览 算法 功能 树结构 特征选择 连续值处理 缺失值处理 剪枝 ID3 分类 多叉树 信息增益 不支持 不支持 不支持 C4.5 分类 多叉树 信息增益比 支持 ...
- ID3\C4.5\CART
目录 树模型原理 ID3 C4.5 CART 分类树 回归树 树创建 ID3.C4.5 多叉树 CART分类树(二叉) CART回归树 ID3 C4.5 CART 特征选择 信息增益 信息增益比 基尼 ...
- 机器学习算法总结(二)——决策树（ID3, C4.5, CART）
决策树是既可以作为分类算法,又可以作为回归算法,而且在经常被用作为集成算法中的基学习器.决策树是一种很古老的算法,也是很好理解的一种算法,构建决策树的过程本质上是一个递归的过程,采用if-then的规 ...
- 机器学习相关知识整理系列之一：决策树算法原理及剪枝（ID3,C4.5,CART）
决策树是一种基本的分类与回归方法.分类决策树是一种描述对实例进行分类的树形结构,决策树由结点和有向边组成.结点由两种类型,内部结点表示一个特征或属性,叶结点表示一个类. 1. 基础知识 熵 在信息学和 ...
- 统计学习五：3.决策树的学习之CART算法
全文引用自<统计学习方法>(李航) 分类与回归树(classification and regression tree, CART)模型是由Breiman等人于1984年提出的另一类决策树 ...
- 决策树与随机森林Adaboost算法
一. 决策树 决策树(Decision Tree)及其变种是另一类将输入空间分成不同的区域,每个区域有独立参数的算法.决策树分类算法是一种基于实例的归纳学习方法,它能从给定的无序的训练样本中,提炼出树 ...
- 机器学习之决策树二-C4.5原理与代码实现
决策树之系列二—C4.5原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9435712.html I ...
随机推荐
- Vue【原创】基于elementui的【分组多选下拉框group-select】
效果图: 如图分为多选模式和单选模式. group-select: 1 <template> 2 <div> 3 <el-select 4 v-model="i ...
- 如何正确实现一个自定义 Exception
最近在公司的项目中,编写了几个自定义的 Exception 类.提交 PR 的时候,sonarqube 提示这几个自定义异常不符合 ISerializable patten. 花了点时间稍微研究了一下 ...
- WPF学习 - 自定义Panel
WPF中的Panel(面板),是继承自FrameworkElement的抽象类,表示一个可以用来排列子元素的面板. 在WPF中,一种预设了几种常用的面板,如Grid.StackPanel.WrapPa ...
- Strimzi Kafka Bridge(桥接)实战之一：简介和部署
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 关于<Strimzi Kafka Bridge( ...
- FX3U-3A-ADP模拟量和数字量之间转换
简单的例子: 0-10V对应0-8,4-20mA对应0-30 以下是对上面例子的详解: 电压: 电压(0-10V) 0-10V对应着数字量0-4000 数字量与变频器HZ量之间的关系是(4000-0) ...
- docker入门加实战——docker安装并配置阿里云加速
docker入门加实战--docker安装并配置阿里云加速 为什么要学习docker 在开发和部署项目的过程中,经常会遇到如下问题: 软件安装包名字复杂,不知道去哪里找 安装软件和部署项目步骤复杂,容 ...
- C++算法之旅、09 力扣篇 | 常见面试笔试题（上）算法小白专用
刷题的目的是为了更好的理解数据结构与算法,更好的理解一些封装起来的库函数是怎么实现的,而不是简简单单的为了刷题而刷题. 时间.空间复杂度 事后统计法 提前写好算法代码和编好测试数据,在计算机上跑,通过 ...
- Jmeter-变量的嵌套使用
场景: 有存在获取到多个登录账号,循环获取单个变量的情况. 常用方法: ${__BeanShell(vars.get("变量字段_${变量字段}"))} 取值示例: 思维扩展: 一 ...
- 浅析Redis大Key
一.背景 在京东到家购物车系统中,用户基于门店能够对商品进行加车操作.用户与门店商品使用Redis的Hash类型存储,如下代码块所示.不知细心的你有没有发现,如果单门店加车商品过多,或者门店过多时,此 ...
- BFF层提升业务性能实际解决方案，以及nodeJs和KOA框架介绍
本文干货满满,介绍了用BFF层(Back-end For Front-end)中间层提升性能的整体解决方案和思路,涉及前期技术调研,聚合业务分析,聚合方法,验收,最后向同学们普及node.koa基础知 ...