反悔贪心&模拟费用流

贪心是一种常用的算法，它能够获得局部最优解，但我们往往需要的是全局最优解，所以我们在贪心的时候加入和反悔的机制，让他能够得到全局最优解。

由于网络流中的退流操作本质上也是反悔贪心，所以在实现反悔贪心时类似费用流的，也会被成为模拟费用流。

一般的实现时在贪心之后加入一个和贪心值相反的值或重构问题使得变成原问题等方式实现。

CF865D Buy Low Sell High

题意：每天可以选择消耗 \(a_i\) 买入一份股票或者获得 \(a_j\) 卖出一份股票（要有股票），或者什么都不做，最大化收益。

这个问题也叫老鼠进洞问题。

我们考虑到达第 \(i\) 天的时候，我们找到前面几天中最小的买入价格 \(a_j\) ，它会对答案做出 \(a_i-a_j\) 的贡献。

但由于一天只能买入一张或者卖出一张，在类似 1 2 100 的结构中贪心就时错误的。

不难发现，如果 \(i\) 会选定 \(j\) 和它做贡献，则在全局最优解中， \(a_j\) 也一定会做贡献。

令 \(a_j\) 与 \(a_k\) 做出 \(a_k-a_j\) 的贡献（ \(j<i<k\) ） 。由于 \(a_k-a_j=a_k-a_i+a_i-a_j\) 。

右式的后两项就是我们贪心的结果，这也就意味着，如果我们再在后面贪心的取一次 \(a_k-a_i\) 即可。

题目有每个数只能买入或卖出一次的限制，所以我们只要在贪心取数的时候额外加入一个 \(a_i\) 即可。

使用小根堆维护最优解，最终复杂度为 \(O(n\log n)\) 。

Luogu P1484 种树

题意：给定一个长为 \(n\) 的序列，从中选 \(k\) 个数不能选相邻的数，最大化加和。

因为不能选择相邻的数，所以在取了最大值 \(a_i\) 的时候， \(a_{i+1}\) 和 \(a_{i-1}\) 就不能选了，但可能全局最优解应该是 \(a_{i+1}+a_{i-1}\) 的。

例如在 \(n=5,k=2\) 时，数据 1 99 100 99 1 可以卡掉纯贪心。

考虑 \(a_{i+1}+a_{i-1}=a_{i}+(a_{i+1}+a_{i-1}-a_{i})\) ，比我们的贪心值多了一个 \(a_{i+1}+a_{i-1}-a_{i}\) 。

但它同时也去多取了一个数，所以考虑 \(a_{i-1},a_i,a_{i+1}\) 三个数在取了 \(a_i\) 后替换成 \(a_{i+1}+a_{i-1}-a_{i}\) 这一个数。

发现这样不影响限制，维护双线链表和大根堆即可。

集训队互测 Round1 Astral Birth

题意：给定一个长为 \(n\) 的 \(01\) 串，询问 \(i=1,2\dots n\) ，将原串分为 \(i\) 的子串后按任意顺序拼接，最长不降子序列的长度的最大值。

不难证明最优答案必然把答案划分成若干个连续的 \(00\dots0\) 或 \(11\dots1\) 。

在分割段数减少的时候，我们需要删去一些连续段来使得损失最小。

我们会发现三个性质：

1. 删去边上的串可以减少一次分割，删去中间的串可以减少一次分割。
2. 删去相邻的两端一定不优。
3. 可以保留一个形如 \(0\dots 01\dots 1\) 的结构。

所以我们需要求的就是看有多少个不相邻的连续段在最终答案中不做贡献，先枚举两端的段取不取，在考虑中间的。

这就变成了类似上一题的做法，负责都为 \(O(n\log n)\) 。

在段数小于 \(3\) 的时候不一定有 \(0\dots 01\dots 1\) 结构，所以需要特判，可以在 \(O(n)\) 的复杂度完成。

CF730I Olympiad in Programming and Sports

题意：每个人有一个数值 \(a_i\) 与 \(b_i\) ，选取 \(p\) 个 \(a_i\) 和 \(s\) 个 \(b_i\) ，两两不等，最大化加和。

用费用流的思想考虑这道题，会发现每个人会有四种状态：

1. 没有被选，准备去编程
2. 没有被选，准备去运动
3. 被选去编程，但想去运动
4. 被选去运动，但想去编程

对于每一种选择，维护一个大根堆，在选择状态 3 或 4 时，需要在 1 或 2 中找一个补齐空缺保证复杂度。

每一次操作后 \(p\) 和 \(s\) 中有一个减少了 \(1\) ，所以最终复杂度为 \(O(n\log n)\) 。

CF280D k-Maximum Subsequence Sum

题意：维护一个序列，支持单点修改和区间内至多k段不相交子段和。

比较经典的 GSS 问题，每次找到区间最大的子段，其对答案做出贡献，然后将区间内的所有值取反。

用线段树维护区间和\最大前缀\最大后缀\最大子区间，复杂度为 \(O(n\log n+m\log n)\) 。

[NEERC2016]Mole Tunnels

题意：给定一个大小为 \(n\) 的树， \(1\) 为根， \(i\) 节点的父亲为 \(\left\lfloor\dfrac{i}{2}\right\rfloor\) 节点，每个点都有 \(c_i\) 的容量，有 \(m\) 次询问，每次额外加入一个鼹鼠，问所有的鼹鼠需要走过总计多少次边才能使每个节点的鼹鼠数量都小于容量。

考虑只有一种鼹鼠时，贪心策略是让鼹鼠走到距离最近的还有值的点，但这时就会出现问题，加入我们取出其中的一条链来看。



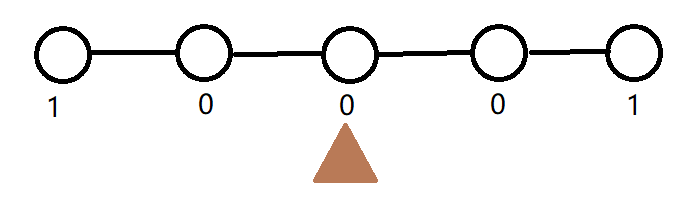
现在在最中间有一个鼹鼠，用贪心的策略，我们假设它选择了往右走两步（如果往左反转之后等效），答案为 \(2\) 。





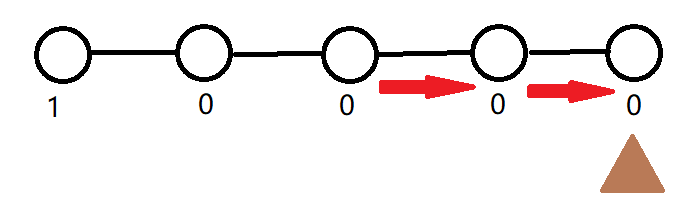
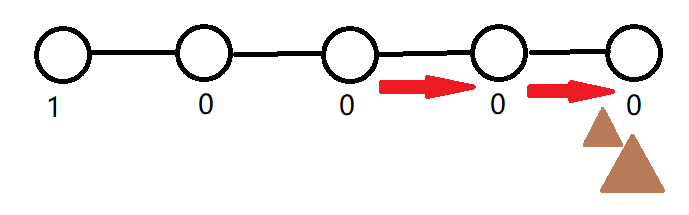
这是又来了一只鼹鼠，刚好在最右边的点，则用贪心的策略它会走向最左边的节点，答案为 \(2+4=6\) 。



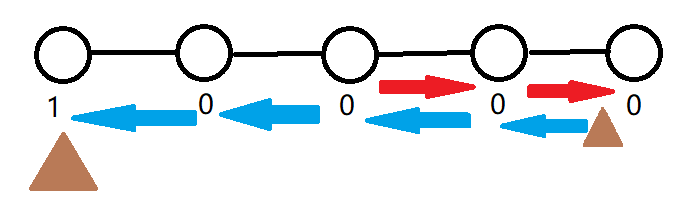
但是我们发现，答案应该而 \(2\) ，而多出来的 \(4\) 就是在于红蓝箭头都走了的两条边。

假如一条边的两端都有一只鼹鼠，交换他们为位置与不交换是等效的，但是浪费了 \(2\) 的步数。

所以我们考虑加入类似网络流中的增广机制，如果一条边 \((u,v)\) 在 \(u\rightarrow v\) 的时候做了 \(1\) 的贡献，则在下次 \(v\rightarrow u\) 的时候，它做 \(-1\) 的贡献抵消掉原来的贡献。

所以我们用一个数组存储每条边目前累计走过的次数和方向即可。

由于树结构为完全二叉树，所以复杂度是 \(O(n\log n)\) 。

[NOI2019] 序列

题意：给定两个序列 \(\{a_n\}\) 与 \(\{b_n\}\) ，分别从两个序列中选出 \(K\) 个元素，要求至少有 \(L\) 个下标 \(a_i\) 和 \(b_i\) 同时被选，最大换选出的元素和。

这样的限制条件很想费用流的模型。

首先考虑转化条件，不好处理至少有 \(L\) 对相同下标，更改为至多有 \(K-L\) 对不相同的。

费用流模型有5种情况：

1. 选取一组下标相同的数。
2. 选取一组下标不同的数，消耗 \(1\) 的不同流量（这个是所有决策中局部最优的）。
3. 选取一组 \(a_i\) 与 \(b_j\) ，且 \(b_i\) 与 \(a_j\) 已经被选，回复 \(1\) 的不同流量。
4. 选取一组 \(a_i\) 与 \(b_j\) ，且 \(b_i\) 已经被选。
5. 选取一组 \(a_i\) 与 \(b_j\) ，且 \(b_i\) 已经被选。

由于不同决策的优先度不同，在满足要求的情况下贪心顺序应为： \(1\rightarrow 3\rightarrow (4,5)\rightarrow 2\) 。

CF335F Buy One, Get One Free

题意：给定一个长为 \(n\) 的序列，你可以一次取出至多两个不相等的数，代价是两个数中的较大值（一个付钱，一个白嫖），最小化代价和。

考虑费用流模型：我们先贪心地从大到小选择和白嫖，如果到后面有更优的决策时，我们会放弃白嫖之前的某一个，而换成给他付钱，然后白嫖另外两个。

由于价格相同的不能同时取，所以考虑将所有价格相同的一起处理。

设白嫖的馅饼价格为 \(k\)，（可能是虚空馅饼）。

如果 \(k<a\)，我们付出 \(k\) 的代价，并白嫖两个 \(a\) 价格馅饼，如果只有一个，我们便空出了一个白嫖的位置。

如果 \(k\geqslant a\)，我们如果不白嫖，我们会有 \(2a\) 的代价，同时获得两个空位；如果我们不白嫖，我们将会有 \(k\) 的代价，同时没有空位。

发现，上面一种情况相当于是有一个代价为 \(2a-k\) 的虚空馅饼抵消了我们选择 \(k\) 的操作。所以此时我们的方案就是，如果 \(2a-k\geqslant 0\) ，我们便消耗 \(k\) 的代价，白嫖了 \(2a-k\) 与 \(k\) 两个馅饼，由于 \(2a-k\leqslant k\) 所以一定会优先消耗馅饼 \(2a-k\) ，不会出现问题。

AT AGC018C Coins

题意：给定 \(n\) 个三元组 \((a_i,b_i,c_i)\)，你需要选择 \(x\) 个 \(a\),\(y\) 个 \(b\)，\(z\) 个 \(c\)（满足 \(x+y+z=n\)），每个三元组中只能选一个，最大化选择的数的和。

考虑每个数先直接选择 \(a_i\) ，然后将 \(b_i,c_i\) 改成 \(b_i-a_i,c_i-a_i\)，题意变为在 \(n\) 个数中选择 \(y\) 个 \(b\)，\(z\) 个 \(c\)，一个下标只能选一次，最大化加和。

考虑费用流模型：

1. 在 \(y\neq 0\) 时，选择 \(b_i\)，\(y\gets y-1\)。
2. 在 \(z\neq 0\) 时，选择 \(c_i\)，\(z\gets z-1\)。
3. 在 \(y\neq 0\) 时，选择 \(c_i\)，同时将已选择的 \(c_j\) 改为 \(b_j\)，\(y\gets y-1\)。
4. 在 \(z\neq 0\) 时，选择 \(b_i\)，同时将已选择的 \(b_j\) 改为 \(c_j\)，\(z\gets z-1\)。

使用四个堆维护即可，复杂度 \(O(n\log n)\)。