Comet OJ - Contest #4 B题 奇偶性

题目链接：https://www.cometoj.com/contest/39/problem/B?problem_id=1577

---

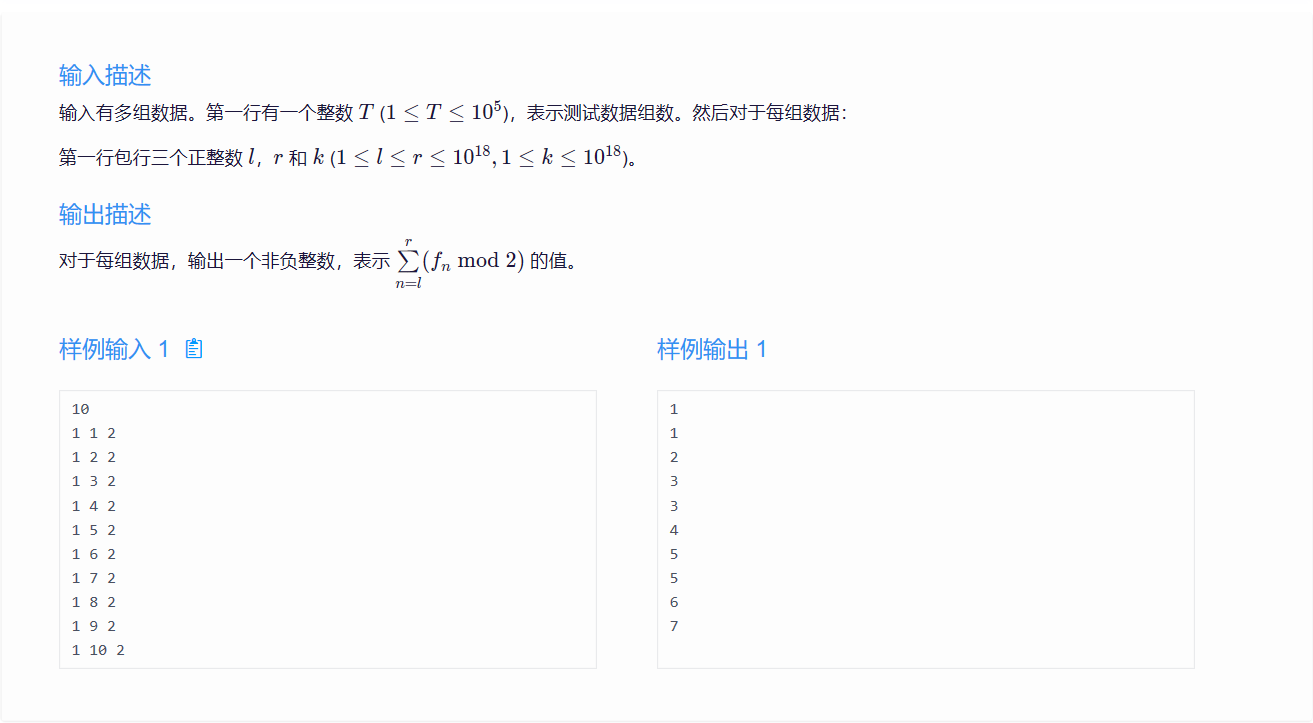
题意：给你一个数列，求L 到 R 区间内 所有数列 （ƒ_n mod 2）的和。

思路：这题是个找规律的题目，首先数列都要对2取模运算，如果这个数是偶数 那么mod 2就是0，奇数就是1，所以这题等价于求 L 到 R 区间内奇数的个数。

　　　1.当 k 为奇数的时候，我们发现数列的值对2取模后全为1，所以 ans = R - L + 1。

　　　2.当 k 为偶数的时候，假设 k = 4，那么：

ƒ0

ƒ1

ƒ2

ƒ3

ƒ4

ƒ5

ƒ6

ƒ7

ƒ8

ƒ9

ƒ10

ƒ11

ƒ12

ƒ13

ƒ14

　　　我们知道偶数个奇数相加和等于偶数，奇数个等于奇数，为了方便我们用 1 表示奇数 用 0 表示偶数。

　　　如图 可以发现循环的规律，我们用除法取模的方法可以算出 1 - n 区间内 0 的节点有 ((n - k) / (k + 1) + 1) 个，所以对 k 所在区间进行分类讨论就好了。

AC代码：

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 int main()
 {
     int n;
     long long l,r,k;
     cin >> n;
     while(n--)
     {
         scanf("%lld%lld%lld",&l,&r,&k);
         long long ans = ;
         if(k %  == )
         {
16
             if(k >= r)
             {
                 if(r == k)
                     ans = r - l;
                 else
                 ans = r - l + ;
             }
             else if(k < l)
             {
                 long long ll,rr;
                 ll = l - ((l - k) / (k + ) + );
                 rr = r - ((r - k) / (k + ) + );
                 ans = rr - ll + ;
             }
             else
             {
                 ans = r - ((r - k) / (k + ) + ) - l + ;
                 if(l == k) ans += ;
             }
         }
         else
         {
             ans = r - l + ;
         }
         printf("%lld\n",ans);
     }
     return ;
 }