ST表——————一失足成千古恨系列2

在此先祝自己这个系列写的越少越好qwq（保证不超过4篇（flag已立））

考试原题：（绝壁是看完复联出的）

第一反应：线段树？？不对，是st表。嗯，没错。哎，st表咋写来着？？完了凉了。

结果：写暴搜的都有60分，结果我爆了0 qwq

80-->0，与键盘无缘嘤嘤嘤

好了开始说正事

ST表用来干什么的？

给定一个区间，求最值。上面那道题是典型的模板题（虽然有毒瘤数据会卡掉st表，但我们这里不讨论）

复杂度：预处理：O(nlogn),询问：O(1)

先说预处理。

st表示一个二维数组，其中st[i][j]表示区间[i,i+2^j-1]中的最值，这里我们就拿最大值举例。显然st[i][0]=a[i],因为[i,i+1-1]中只有i一个点。那么我们怎么推其他的st[i][j]呢？

我们先来看一张图

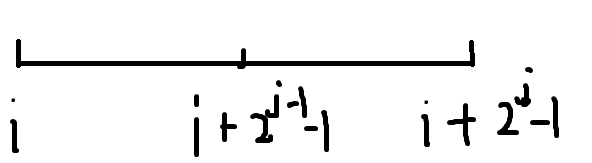
这样我们就可以推出来：st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]。为什么呢？因为i+2^(j-1)+2^(j-1)-1=i+2*(2^(j-1))-1=i+2^j-1

这样，我们就可以预处理出来所有的st[i][j]了

int st[maxn][]//一般第二维不会超过20，这里是应对毒瘤数据范围
void init()
{
    for(int i=;i<=n;i++)
        st[i][]=a[i];
    for(int  i=;(<<i)<=n;i++)//这里实际上枚举上面说的j
    {for(int j=;j+(<<i)-<n;j++)
       {st[j][i]=max(st[j][i-],st[j+(<<(i-))][i-]);//这里为什么j是第一维呢？这里我们max()里面变的只有第一维，所以我们要先处理第一维，才能保证后面正常进行（就是个顺序问题）
        }
    }
}

查询给的区间可不是卡好2^k的，所以我们应该怎么查询呢？我们第二维表示的是i+2^j-1,我们看到这里有个次方，我们可以玄学的考虑一下log。（以2为底）

这里区间的长度显然是2^j,我们已经考虑到log，那不妨对区间长度len=2^j来个log.（向下取整），设t=log(len)/log(2)向下取整，那么2^t一定<len/2。我们发现，l+2^t一定是在[l,r]的中间往右，而r-2^t一定在中间往左。[l,l+2^t-1]与[r-2^t+1,r]这两个区间是可以完全覆盖[l,r]，而且还不会有超出[l,r]的部分，所以我们就可以从st[l][t]和st[r-2^t+1][t]中选一个最大值。

Update

---

由于窝之前的代码是手糊的，所以出了锅。误导了您真的十分十分抱歉（我发4再也不手糊代码了qwq）

真·能AC板子的代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
#define pa pair<int,int>
#include<ctime>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=;
inline ll read()
{
    char ch=getchar();
    ll x=;
    bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-') f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
int n,m,a[],st[][];
int lg[];
int qry(int l,int r)
{
    int qwq=log((double)(r-l+))/log(2.0);
    return max(st[l][qwq],st[r-(<<qwq)+][qwq]);
}
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        a[i]=read();
        st[i][]=a[i];
    }
    for(int i=;(<<i)<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            st[j][i]=max(st[j][i-],st[j+(<<(i-))][i-]);
        }
    }
    while(m--)
    {
        int l=read(),r=read();
        printf("%d\n",qry(l,r));
    }
}