[CF804F]Fake bullions

Solution:

​ 这题可以分为两个部分，

​ 一个部分为处理出每个点最大的金条数与最小的金条数，记为 \([Min_i, Max_i]\)

​ 第二部分为对于 \(n\) 个变量 \(x_i\in[Min_i, Max_i]\cup \mathbb {Z}\)，计算选出 \(B\) 个前 \(A\) 大变量的方案数。

​ 对于两个点 u->v ，如果有 u 的人 i (有金条) 与 v 的人 j 满足 \(i\equiv j(\text{mod }\gcd(S_u, S_v))\) ，那么 i 就可以给 j 假金条。

​ 同理，对于一条路径 u->...->v 设 g 为其 \(\gcd\) ，那么只要满足 \(i \equiv j(\text{mod }g)\) ，那么 i 就可以给 j 假金条。

​ 所以对于一个强连通分量中，有金条的人就会满足 \(i\equiv j(\text{mod } g)\) ，j 为每个点有金条的人，g为整个强连通分量的 \(\gcd\) 。

​ 枚举一个点有金条的人，这样就可以 \(O(\text{金条数目})\) 求出每一个强连通分量的金条拥有状态。

​ 由竞赛图的性质，缩点后的竞赛图还是竞赛图，而且会长这个样子：

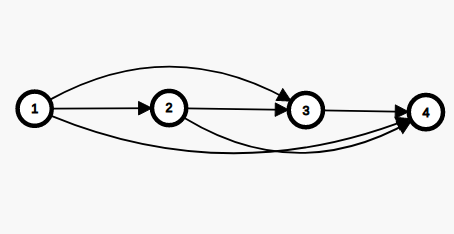
​ 即每个点都向它后面连边，显然我们为了让金条数量最大化就是按照拓扑序依次算点的贡献，这样算出来每个强连通分量的金条数假设为 Mx 那么每个点u拥有的金条数就是\(\frac{S_uMx}{g}\)。

​ 接下来就考虑怎么计数，为了不算重，枚举 u 为B中最小的点，然后统计出 \(Max_u<Min_i\) 的数量 \(cnt_1\)，以及 \(Max_i\geq Max_u\geq Min_i\) 的数量 \(cnt_2\)，那么再枚举在 \(cnt_2\)个中选j个，给答案加上 \({~cnt_2~\choose j}{~cnt_1~\choose B - 1 - j}\)。

#include <iostream>
#include <cstdio>
#include <set>
#include <algorithm>
#include <vector>
#define LL long long
using namespace std;
const int maxn = 5003;
const int MOD = 1e9 + 7;
vector<int> g[maxn];
vector<bool> city[maxn];
int A, B, n;
int s[maxn], fac[maxn], ifac[maxn];
void input() {
    char str[(int)(2e6) + 2];
    scanf("%d %d %d", &n, &A, &B);
    for (int i = 1; i <= n; ++i) {
        scanf("%s", str + 1);
        for (int j = 1; j <= n; ++j)
            if (str[j] == '1')
                g[i].push_back(j);
    }
    for (int i = 1; i <= n; ++i) {
        scanf("%d %s", &s[i], str);
        city[i].resize(s[i]);
        for (int j = 0; j < s[i]; ++j)
            city[i][j] = str[j] - '0';
    }
}
LL qpow(LL a, LL b) {
    LL res(1);
    while (b) {
        if (b & 1) {
            res = res * a % MOD;
        }
        a = a * a % MOD;
        b >>= 1;
    }
    return res;
}
void init() {
    fac[0] = 1;
    int N = maxn - 3;
    for (int i = 1; i <= N; ++i)
        fac[i] = 1ll * fac[i - 1] * i % MOD;
    ifac[N] = qpow(fac[N], MOD - 2);
    for (int i = N - 1; i >= 0; --i)
        ifac[i] = 1ll * ifac[i + 1] * (i + 1) % MOD;
}
vector<bool> colbull[maxn];
int Gcdcol[maxn], cntbull[maxn], maxbull[maxn], minbull[maxn];
int low[maxn], dfn[maxn], dfst, col[maxn], colcnt, stk[maxn], top;
void tarjan(int u) {
    dfn[u] = low[u] = ++dfst;
    stk[++top] = u;
    for (int i = 0; i < (int)g[u].size(); ++i) {
        int v= g[u][i];
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (!col[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u]) {
        ++colcnt;
        int v;
        do {
            v = stk[top--];
            col[v] = colcnt;
        } while (u != v);
        Gcdcol[colcnt] = s[u];
    }
}
void solve1() {
    for (int i = 1; i <= n; ++i)
        if (!dfn[i])
            tarjan(i);
    for (int i = 1; i <= n; ++i)
        Gcdcol[col[i]] = __gcd(Gcdcol[col[i]], s[i]);
    for (int i = 1; i <= n; ++i)  {
        colbull[col[i]].resize(Gcdcol[col[i]]);
        for (int j = 0; j < s[i]; ++j)
            if (city[i][j] == 1) {
                colbull[col[i]][j % Gcdcol[col[i]]] = 1;
            }
    }
    vector<bool> tmp;
    for (int i = colcnt; i >= 2; --i) {
        int g = __gcd(Gcdcol[i], Gcdcol[i - 1]);
        tmp.clear();
        tmp.resize(g);
        for (int j = 0; j < Gcdcol[i]; ++j)
            tmp[j % g] = tmp[j % g] | colbull[i][j];
        for (int j = 0; j < Gcdcol[i - 1]; ++j)
            colbull[i - 1][j] = colbull[i - 1][j] | tmp[j % g];
    }
    for (int i = 1; i <= colcnt; ++i)
        for (int j = 0; j < Gcdcol[i]; ++j)
            cntbull[i] += colbull[i][j];
    for (int i = 1; i <= n; ++i)
        maxbull[i] = s[i] / Gcdcol[col[i]] * cntbull[col[i]];
    for (int i = 1; i <= n; ++i)
        for (int j = 0; j < s[i]; ++j)
            minbull[i] += city[i][j];
}
LL ans;
LL combine(int n, int m) {
    if (m < 0 || n < 0 || m > n) return 0;
    return 1ll * fac[n] * ifac[m] % MOD * ifac[n - m] % MOD;
}
void solve2() {
    for (int i = 1; i <= n; ++i) {
        int cnt1 = 0, cnt2 = 0;
        for (int j = 1; j <= n; ++j) {
            if (i == j) continue;
            if (minbull[j] > maxbull[i]) ++cnt1;
            else if (maxbull[j] > maxbull[i] || (maxbull[j] == maxbull[i] and j < i)) ++cnt2;
        }
        if (cnt1 >= A) continue;
        for (int j = min(B - 1, min(cnt2, A - 1 - cnt1)); j >= B - cnt1 - 1 && j >= 0; j--) {
            ans = (1ll * ans + 1ll * combine(cnt1, B - j - 1) * combine(cnt2, j) % MOD) % MOD;
        }
    }
    cout << ans << endl;
}
int main() {
   // freopen("fake.in", "r", stdin);
   // freopen("fake.out", "w", stdout);
    input();
    init();
    solve1();
    solve2();
    return 0;
}