001-spring boot概述与课程概要

一、Spring Boot介绍

　　Spring Boot的目的在于创建和启动新的基于spring框架的项目。Spring boot会选择最适合的Spring 子项目和第三方开源库进行整合。大部分Spring boot应用只需要非常少的配置就可以快速运行起来。
　　Spring Boot 是伴随着Spring4.0诞生的。
　　Spring Boot提供了一种快速使用Spring的方式

　　

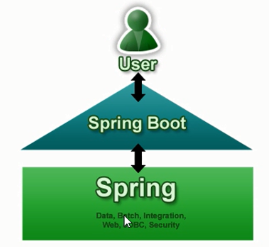
　　在开始的Spring 开发中，需要引入大量的xml，在spring 2.5引入包扫描，消除显式的配置Bean，spring 3.0又引入了基于javabean的配置，这种方式可以取代xml文件【@Component】，尽管如此，在实际的开发中还是需要配置xml，如spring mvc的配置，事务管理器。过滤器、切面等。包依赖管理等问题

　　springboot致力于解决以上问题。

二、Spring Boot特点

1、为基于Spring的开发提供更快的入门体验

2、创建可以独立运行的Spring应用

3、直接嵌入Tomcat或Jetty服务器，不需要打包成war

4、提供推荐的基础POM文件（starter）来简化Apache maven配置

5、尽可能的更具项目依赖来自动配置Spring框架

6、提供可以直接在生产环境中使用的功能，如性能指标、应用信息和应用健康检查

7、开箱即用、没有代码生成，也无需XML配置。同时也可以修改默认值来满足特定的需求

8、其他大量项目都是基于Spring boot之上的，如SPring Cloud【一系列的分布式功能，微服务，等】

备注：是、使编码、配置、部署、监控变得简单。

自动配置，起步依赖，Actuator对运行状态监控

三、Spring Boot缺点

1、依赖太多，随便的一个Spring boot应用都好大

2、缺少服务的注册和发现等解决方案

3、缺少监控继承方案、安全管理方案

4、缺少中文文档

四、Spring Boot应用场景

1、Spring能够应用的场景

2、java web应用

3、微服务

五、目录

1、Spring4 快速入门

2、Spring4扩展分析

3、Spring Boot快速入门

4、Spring Boot配置分析

5、Spring Boot自动配置

6、Spring Boot @Enable*注解的工作原理

7、Spring Boot @EnableAutoConfiguration深入分析

8、Spring Boot 事件监听

9、Spring Boot 扩展分析

10、Spring Boot 运行流程分析

11、Spring Boot web

12、Spring Boot 定制和优化内嵌的Tomcat

13、Spring Boot jdbc

14、Spring Boot aop

15、Spring Boot Starter

16、Spring Boot 日志

17、Spring Boot 监控和度量

18、Spring Boot 测试

19、Spring Boot 构建微服务实战

20、Spring Boot 服务的注册和发现

21、Spring Boot 应用的打包和部署

六、使用的软件

Eclipse 【https://www.eclipse.org/downloads/eclipse-packages/】

Apache maven【http://maven.apache.org/download.cgi】

JDK 1.8

　　配置JAVA_HOME 变量：E:\ProgramFiles\Java\jdk1.8.0_25

　　配置path变量：;%JAVA_HOME%\bin

　　[1.5后不是必须]配置classpath变量 需要配置tools.jar，dt.jar：.;%JAVA_HOME%\lib\tools.jar;%JAVA_HOME%\lib\dt.jar

Spring Boot 1.5.9 Release

Spring 4.3.13

spring4可以兼容jdk1.6，但是spring boot官方公布的一些功能使用1.8性能会高很多，这里使用1.8