[CSP-S模拟测试]:赤壁情（DP）

前赤壁赋

　　壬戌之秋，七月既望，苏子与客泛舟游于赤壁之下。清风徐来，水波不兴。举酒属客，诵明月之诗，歌窈窕之章。少焉，月出于东山之上，徘徊于斗牛之间。白露横江，水光接天。纵一苇之所如，凌万顷之茫然。浩浩乎如冯虚御风，而不知其所止；飘飘乎如遗世独立，羽化而登仙。
于是饮酒乐甚，扣舷而歌之。歌曰：“桂棹兮兰桨，击空明兮溯流光。渺渺兮予怀，望美人兮天一方。”客有吹洞箫者，倚歌而和之。其声呜呜然，如怨如慕，如泣如诉；余音袅袅，不绝如缕。舞幽壑之潜蛟，泣孤舟之嫠妇。
　　苏子愀然，正襟危坐，而问客曰：“何为其然也？”客曰：“‘月明星稀，乌鹊南飞。’此非曹孟德之诗乎？西望夏口，东望武昌，山川相缪，郁乎苍苍，此非孟德之困于周郎者乎？方其破荆州，下江陵，顺流而东也，舳舻千里，旌旗蔽空，酾酒临江，横槊赋诗，固一世之雄也，而今安在哉？况吾与子渔樵于江渚之上，侣鱼虾而友麋鹿，驾一叶之扁舟，举匏樽以相属。寄蜉蝣于天地，渺沧海之一粟。哀吾生之须臾，羡长江之无穷。挟飞仙以遨游，抱明月而长终。知不可乎骤得，托遗响于悲风。”
　　苏子曰：“客亦知夫水与月乎？逝者如斯，而未尝往也；盈虚者如彼，而卒莫消长也。盖将自其变者而观之，则天地曾不能以一瞬；自其不变者而观之，则物与我皆无尽也，而又何羡乎!且夫天地之间，物各有主，苟非吾之所有，虽一毫而莫取。惟江上之清风，与山间之明月，耳得之而为声，目遇之而成色，取之无禁，用之不竭。是造物者之无尽藏也，而吾与子之所共适。”
　　客喜而笑，洗盏更酌。肴核既尽，杯盘狼籍。相与枕藉乎舟中，不知东方之既白。

---

题目传送门（内部题30）

---

输入格式

第一行包含三个非负整数$N,M$和$K,N$，$M$意义如上，$K$为小数点后保留位数。

---

输出格式

包含一个小数点后$K$位的实数，注意四舍五入。

---

样例

样例输入：

3 3 3

样例输出：

0.667

---

数据范围与提示

样例解释：

$N=3$的排列有$6$个：$123,132,213,231,312,321$；他们的波动强度分别为$2,3,3,3,3,2$。
所以，赤壁之意不小于$3$的概率是$\frac{4}{6}$，即$0.667$。
你也可以通过下面的代码来验证这个概率：

int a[3]={0,1,2}, s=0, n=3;
for (int i=0; i<1000000; i++){
random_shuffle(a,a+n);
int t=0;
for (int j=0; j<n-1; j++) t += abs(a[j+1]-a[j]);
if (t>=3) s++;
}
printf("%.3f\n",s/1000000.0);

数据范围：

---

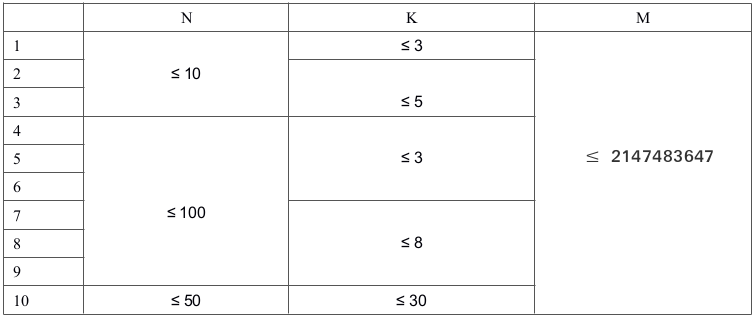
题解

这也许是我见过最恶心的题了……

你看着数据范围，保留$30$位小数，__float128，自闭了。

言归正转，开始说题解。

我们从大到小依次插入这些数。

还是考虑$DP$，设$dp[i][j][k][l]$表示插到了第$i$个数，当前对答案的贡献为$j$，加入数字形成了$k$段数，边界上已经有了$l$个数的方案数。

什么玩意儿这是？

我来解释一下，$i,j$就不做过多解释了，都懂。

先来解释$k$，如下图中，蓝色区域为整个序列，橙色区域为已经填了数的区域，那么下面就有$4$段数，$k$为$4$：

在来解释一下$l$，分为以下四种情况：

边界处没有数，$l=0$：

左边界有数，$l=1$：

右边界有数，$l=1$，但是在统计方案数的时候可以与上面的情况归在一起，毕竟序列可以从左往右，也可以从右往左：

两边都有数，$l=2$：

现在解释完了$DP$的意义，那么先不要考虑转移，先来考虑在插入$i$的时候的贡献。

为简化问题，也为了你能更好的理解下面式子的意义，我们在插入一个数的时候，可以先将它的贡献加上，然后再在它旁边插入一个数的时候减去。

那么，分为一下三种情况：

　　$\alpha.$若数字$i$加入时新加入一个段，那数字$i$的贡献是$-2\times i$，因为如果新开了一段，这个数字两边的数肯定要比这个数字大。
　　$\beta.$若数字$i$加入时段数没有改变，则$i$对波动程度没有影响，因为一边数字已加，另一边数字没有加，$i$的贡献$=-i+i$。
　　$\gamma.$若数字$i$加入时将两段数合并，那数字$i$个贡献数$2\times i$，因为$i$两边的数已加，且比$i$小。

现在可以考虑转移了，列出$13$个状态转移方程……

$dp[i][j-i\times 2][k+1][0]+=dp[i-1][j][k][0]\times (k+1)$

　　在中间插入一段新的，且没有段在边界：　　

$dp[i][j][k][0]+=dp[i-1][j][k][0]\times k\times 2$

　　挨着插，且没有段在边界：　　

$dp[i][j+i\times 2][k-1][0]+=dp[i-1][j][k][0]\times (k-1)$

　　合并两段，且没有段在边界：

$dp[i][j-i][k+1][1]+=dp[i-1][j][k][0]\times 2$

　　在边界上增加一段，且另一个边界没有：

$dp[i][j+i][k][1]+=dp[i-1][j][k][0]\times 2$

　　连接一段和边界：

$dp[i][j-i\times 2][k+1][1]+=dp[i-1][j][k][1]\times k$

　　有一段在边界，再添加一个不在边界上的新段：

$dp[i][j][k][1]+=dp[i-1][j][k][1]\times (k\times 2-1)$

　　有一段在边界，挨着一段添加一个：

$dp[i][j+i\times 2][k-1][1]+=dp[i-1][j][k][1]\times (k-1)$

　　有一段在边界，添加的时候合并了两段：

$dp[i][j-i][k+1][2]+=dp[i-1][j][k][1]$

　　有一段在边界上，再添加一段新的在另一个边界上：

$dp[i][j+i][k][2]+=dp[i-1][j][k][1]$

　　有一个在边界上，添加一个让一段与另一个边界相连：

$dp[i][j-i\times 2][k+1][2]+=dp[i-1][j][k][2]\times (k-1)$

　　有两个在边界上，添加一个新段：

$dp[i][j][k][2]+=dp[i-1][j][k][2]\times (k\times 2-2)$

　　有两个在边界上，挨着一段添加一个：

$dp[i][j+i\times 2][k-1][2]+=dp[i-1][j][k][2]\times (k-1)$

　　有两个在边界上，添加一个合并两段：

状态转移以及解释就这么多了

注意需要打数据点分治，最后一个点再用__float128，否则会超时。

至于$m$非常大，其实并没有什么关系。因为$n$最大是$100$，那么$m$太大了也没有用。自己定义一个最大值就好。不用写高精度。

时间复杂度：$\Theta(24000\times n^2)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m,K;
int maxn[101];
bool pos;
double dp13[2][17000][101][3],ans13;
__float128 dp02[2][17000][101][3],ans02;
int sta[31];
int floor(__float128 x){for(int i=9;i>=0;--i)if(x>=i)return i;}
void print__float128(__float128 x,int ws)
{
	for(int i=1;i<=ws;++i)x*=10,sta[i]=floor(x),x-=floor(x);
	x*=10;if(floor(x)>=5)sta[ws]++;
	for(int i=ws;i;--i)if(sta[i]==10)sta[i]=0,sta[i-1]++;
	if(!ws){printf("%d",sta[0]);return;}
	printf("%d.",sta[0]);
	for(int i=1;i<=ws;++i)printf("%d",sta[i]);
}
int main()
{
	scanf("%d%d%d",&n,&m,&K);
	if(K<=8)
	{
		dp13[0][7998][1][0]=1;
		dp13[0][7999][1][1]=2;
		dp13[0][8000][1][2]=1;
		for(int i=1;i<=n;i++)maxn[i]=min(i,n-i+1);
		for(int i=2;i<=n;i++)
		{
			int size=min(8000,i*(i+1));
			pos^=1;
			for(int k=1;k<=maxn[i];k++)
				for(int j=-size+8000;j<=size+8000;j++)
					dp13[pos][j][k][0]=dp13[pos][j][k][1]=dp13[pos][j][k][2]=0;
			for(int k=1;k<=maxn[i-1];k++)
				for(int j=-size+8000;j<=size+8000;j++)
				{
					dp13[pos][j-i*2][k+1][0]+=dp13[!pos][j][k][0]*(k+1);
					dp13[pos][j][k][0]+=dp13[!pos][j][k][0]*k*2;
					dp13[pos][j+i*2][k-1][0]+=dp13[!pos][j][k][0]*(k-1);
					dp13[pos][j-i][k+1][1]+=dp13[!pos][j][k][0]*2;
					dp13[pos][j+i][k][1]+=dp13[!pos][j][k][0]*2;
					dp13[pos][j-i*2][k+1][1]+=dp13[!pos][j][k][1]*k;
					dp13[pos][j][k][1]+=dp13[!pos][j][k][1]*(k*2-1);
					dp13[pos][j+i*2][k-1][1]+=dp13[!pos][j][k][1]*(k-1);
					dp13[pos][j-i][k+1][2]+=dp13[!pos][j][k][1];
					dp13[pos][j+i][k][2]+=dp13[!pos][j][k][1];
					dp13[pos][j-i*2][k+1][2]+=dp13[!pos][j][k][2]*(k-1);
					dp13[pos][j][k][2]+=dp13[!pos][j][k][2]*(k*2-2);
					dp13[pos][j+i*2][k-1][2]+=dp13[!pos][j][k][2]*(k-1);
				}
		}
		for(int i=m+8000;i<=16999;i++)
			ans13+=dp13[pos][i][1][2];
		for(int i=1;i<=n;i++)ans13/=i;
		switch(K)
		{
			case 0:printf("%lf",ans13);break;
			case 1:printf("%.1lf",ans13);break;
			case 2:printf("%.2lf",ans13);break;
			case 3:printf("%.3lf",ans13);break;
			case 4:printf("%.4lf",ans13);break;
			case 5:printf("%.5lf",ans13);break;
			case 6:printf("%.6lf",ans13);break;
			case 7:printf("%.7lf",ans13);break;
			case 8:printf("%.8lf",ans13);break;
		}
	}
	else
	{
		dp02[0][7998][1][0]=1;
		dp02[0][7999][1][1]=2;
		dp02[0][8000][1][2]=1;
		for(int i=1;i<=n;i++)maxn[i]=min(i,n-i+1);
		for(int i=2;i<=n;i++)
		{
			int size=min(8000,i*(i+1));
			pos^=1;
			for(int k=1;k<=maxn[i];k++)
				for(int j=-size+8000;j<=size+8000;j++)
					dp02[pos][j][k][0]=dp02[pos][j][k][1]=dp02[pos][j][k][2]=0;
			for(int k=1;k<=maxn[i-1];k++)
				for(int j=-size+8000;j<=size+8000;j++)
				{
					dp02[pos][j-i*2][k+1][0]+=dp02[!pos][j][k][0]*(k+1);
					dp02[pos][j][k][0]+=dp02[!pos][j][k][0]*k*2;
					dp02[pos][j+i*2][k-1][0]+=dp02[!pos][j][k][0]*(k-1);
					dp02[pos][j-i][k+1][1]+=dp02[!pos][j][k][0]*2;
					dp02[pos][j+i][k][1]+=dp02[!pos][j][k][0]*2;
					dp02[pos][j-i*2][k+1][1]+=dp02[!pos][j][k][1]*k;
					dp02[pos][j][k][1]+=dp02[!pos][j][k][1]*(k*2-1);
					dp02[pos][j+i*2][k-1][1]+=dp02[!pos][j][k][1]*(k-1);
					dp02[pos][j-i][k+1][2]+=dp02[!pos][j][k][1];
					dp02[pos][j+i][k][2]+=dp02[!pos][j][k][1];
					dp02[pos][j-i*2][k+1][2]+=dp02[!pos][j][k][2]*(k-1);
					dp02[pos][j][k][2]+=dp02[!pos][j][k][2]*(k*2-2);
					dp02[pos][j+i*2][k-1][2]+=dp02[!pos][j][k][2]*(k-1);
				}
		}
		for(int i=m+8000;i<=16999;i++)
			ans02+=dp02[pos][i][1][2];
		for(int i=1;i<=n;i++)ans02/=i;
		print__float128(ans02,K);
	}
	return 0;
}

---

rp++