c++实验10 图的应用实验
大体与上次实验相同，特点为图是邻接表存储结构
--博客后半部分有程序的所有代码--
1、图邻接表存储结构表示及基本操作算法实现
所加载的库函数或常量定义及类的定义：
#include "SeqQueue.h"
const int MaxVertices = ;
const int MaxWeight=;
（1）邻接表存储结构类定义：
struct EdgeType
{
int dest;
DistT weight;
EdgeType *next; EdgeType(){};
EdgeType(int d, DistT w): dest(d), weight(w), next(NULL){}
};
struct ItemType
{
VerT data;
EdgeType *adj;
}; class AdjTWGraph
{
private:
ItemType Vertices[MaxVertices];
int numVertices;
double numOfEdges; void DepthFirstSearch(const int v, int visited[]);
void BroadFirstSearch(const int v, int visited[]);
public:
AdjTWGraph(void);
~AdjTWGraph(void); int NumOfVertices(void)
{return numVertices;}
double NumOfEdges(void)
{return numOfEdges;}
VerT GetValue(const int i);
int GetWeight(const int v1, const int v2);
void Show(); //输出邻接矩阵结果
void InsertVertex(const VerT &vertex);
void InsertWayEdge(const int v1, const int v2, int weight);
void InsertNoWayEdge(const int v1, const int v2, int weight);
void DeleteVertex(const int v);
void DeleteEdge(const int v1, const int v2); int GetFirstNeighbor(const int v);
int GetNextNeighbor(const int v1, const int v2); void DepthFirstSearch();
void BroadFirstSearch();
};
（2）创建邻接表算法
创建无向网邻接表算法：
void CreatNoWayWeb(AdjTWGraph &G, DataType V[],int n,RowColWeight E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向网参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight);
G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight);
}
}
创建有向网邻接表算法：
void CreatWayWeb(AdjTWGraph &G, DataType V[], int n,RowColWeight E[],int e)
//在图G中插入n个顶点V和e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]); //在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col, E[k].weight);
}
（3）输出邻接表结果算法
void AdjTWGraph::Show()
{
for(int i=;i<numVertices;i++)
{
for(int j=;j<numVertices;j++)
{
int a=GetWeight(i,j);
if(a==MaxWeight)
cout<<"∞ ";
else
cout<<a<<" ";
}
cout<<endl;
}
}
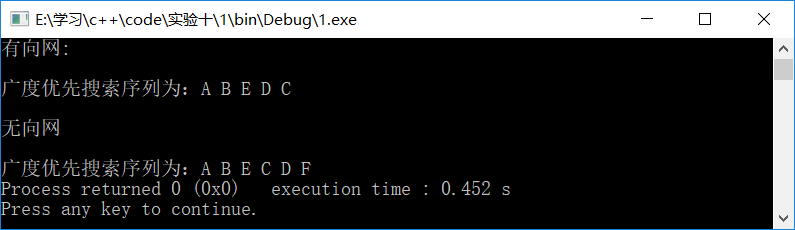
测试结果粘贴如下：
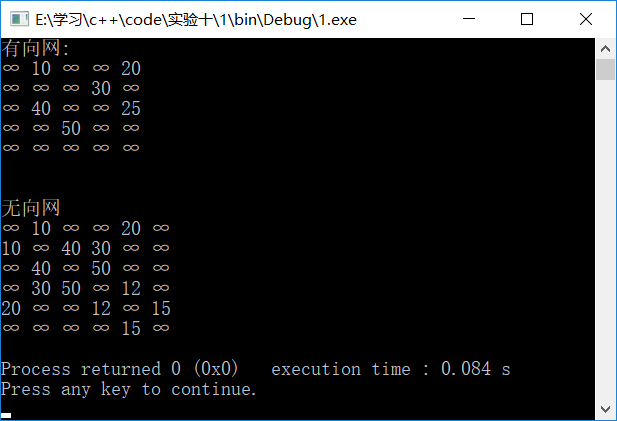
2、图的遍历递归算法
（1）（存储结构为邻接表）深度优先遍历算法-递归算法
void AdjTWGraph::DepthFirstSearch()
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++) visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(! visited[i])
DepthFirstSearch(i, visited);
delete []visited;
} void AdjTWGraph::DepthFirstSearch(const int v, int visited[])
{
cout<<GetValue(v)<<" ";
visited[v] = ; int w = GetFirstNeighbor(v);
while(w != -)
{
if(! visited[w])
DepthFirstSearch(w, visited);
w = GetNextNeighbor(v, w);
}
}
测试结果粘贴如下：
int main()
{
AdjTWGraph g,f;
char a[] = {'A','B','C','D','E'};
char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{,,},{,,},{,,},{,,},{,,},{,,}};
RowColWeight r2[] ={{,,},{,,},{,,},{,,},{,,},{,,},{,,}};
int n1,n2,e1,e2;
n1=sizeof(a)/sizeof(a[]);
n2=sizeof(b)/sizeof(b[]);
e1=sizeof(r1)/sizeof(r1[]);
e2=sizeof(r2)/sizeof(r2[]);
CreatWayWeb(g, a, n1, r1, e1); //创建有向网
CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl;
cout << "\n深度优先搜索序列为：";
g.DepthFirstSearch();
cout<<"\n\n无向网"<<endl;
cout << "\n深度优先搜索序列为：";
f.DepthFirstSearch();
return ;
}
有向网/无向网的测试结果：
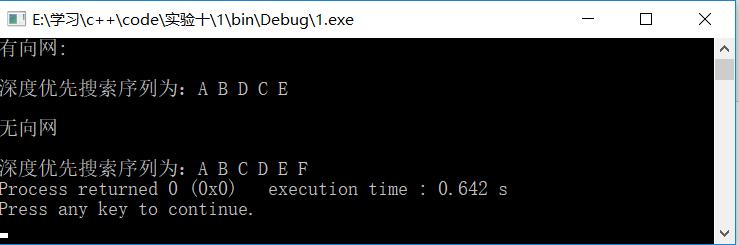
（2）广度优先遍历算法（递归算法）
void AdjTWGraph::BroadFirstSearch()
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++) visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(!visited[i]) BroadFirstSearch(i, visited);
delete []visited;
} void AdjTWGraph::BroadFirstSearch(const int v, int visited[])
{
VerT u, w;
SeqQueue queue;
cout<<GetValue(v)<<" ";
visited[v] = ;
queue.Append(v);
while(queue.NotEmpty())
{
u = queue.Delete();
w = GetFirstNeighbor(u);
while(w != -)
{
if(!visited[w])
{
cout<<GetValue(w)<<" ";;
visited[w] = ;
queue.Append(w);
}
w = GetNextNeighbor(u, w);
}
}
}
测试结果粘贴如下：
int main()
{
AdjTWGraph g,f;
char a[] = {'A','B','C','D','E'};
char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{,,},{,,},{,,},{,,},{,,},{,,}};
RowColWeight r2[] ={{,,},{,,},{,,},{,,},{,,},{,,},{,,}};
int n1,n2,e1,e2;
n1=sizeof(a)/sizeof(a[]);
n2=sizeof(b)/sizeof(b[]);
e1=sizeof(r1)/sizeof(r1[]);
e2=sizeof(r2)/sizeof(r2[]);
CreatWayWeb(g, a, n1, r1, e1); //创建有向网
CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl;
cout << "\n广度优先搜索序列为：";
g.BroadFirstSearch();
cout<<"\n\n无向网"<<endl;
cout << "\n广度优先搜索序列为：";
f.BroadFirstSearch();
return ;
}
有向网/无向网的测试结果：
最后附上整体代码结构与结果
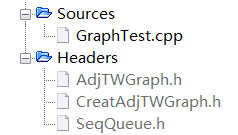
AdjTWGraph.h
#include "SeqQueue.h"
const int MaxVertices = ;
const int MaxWeight=;
struct EdgeType
{
int dest;
DistT weight;
EdgeType *next; EdgeType(){};
EdgeType(int d, DistT w): dest(d), weight(w), next(NULL){}
};
struct ItemType
{
VerT data;
EdgeType *adj;
}; class AdjTWGraph
{
private:
ItemType Vertices[MaxVertices];
int numVertices;
double numOfEdges; void DepthFirstSearch(const int v, int visited[]);
void BroadFirstSearch(const int v, int visited[]);
public:
AdjTWGraph(void);
~AdjTWGraph(void); int NumOfVertices(void)
{return numVertices;}
double NumOfEdges(void)
{return numOfEdges;}
VerT GetValue(const int i);
int GetWeight(const int v1, const int v2);
void Show(); //输出邻接矩阵结果
void InsertVertex(const VerT &vertex);
void InsertWayEdge(const int v1, const int v2, int weight);
void InsertNoWayEdge(const int v1, const int v2, int weight);
void DeleteVertex(const int v);
void DeleteEdge(const int v1, const int v2); int GetFirstNeighbor(const int v);
int GetNextNeighbor(const int v1, const int v2); void DepthFirstSearch();
void BroadFirstSearch();
}; AdjTWGraph::AdjTWGraph(void)
{
for(int i = ; i < MaxVertices; i++) Vertices[i].adj = NULL;
numVertices = ;
numOfEdges = ;
} AdjTWGraph::~AdjTWGraph(void)
{
for(int i = ; i < numVertices; i++)
{
EdgeType *p = Vertices[i].adj, *q;
while(p != NULL)
{
q = p->next;
delete p;
p = q;
}
}
} VerT AdjTWGraph::GetValue(const int i)
{
if(i < || i > numVertices)
{
cout << "参数i越界出错!" << endl;
exit();
}
return Vertices[i].data;
} int AdjTWGraph::GetWeight(const int v1, const int v2)
{ if(v1 < || v1 > numVertices || v2 < || v2 > numVertices)
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
EdgeType *p = Vertices[v1].adj;
while(p != NULL && p->dest < v2)
p = p->next;
if(p==NULL||v2 != p->dest)
{
return MaxWeight;
}
return p->weight;
} void AdjTWGraph::InsertVertex(const VerT &vertex)
{
Vertices[numVertices].data = vertex;
numVertices++;
} void AdjTWGraph::InsertWayEdge(const int v1, const int v2, int weight)
{
if(v1 < || v1 > numVertices || v2 < || v2 > numVertices)
{
cout << "参数v1或v2越界出错!" << endl;
exit();
} EdgeType *q = new EdgeType(v2, weight);
if(Vertices[v1].adj == NULL)
Vertices[v1].adj = q;
else
{
EdgeType *curr = Vertices[v1].adj, *pre = NULL;
while(curr != NULL && curr->dest < v2)
{
pre = curr;
curr = curr->next;
}
if(pre == NULL)
{
q->next = Vertices[v1].adj;
Vertices[v1].adj = q;
}
else
{
q->next = pre->next;
pre->next = q;
}
}
numOfEdges++;
}
void AdjTWGraph::InsertNoWayEdge(const int v1, const int v2, int weight)
//插入一条起始顶点为v1、终止顶点为 v2、权值为weight的边
{
if(v1 < || v1 > numVertices || v2 < || v2 > numVertices)
{
cout << "参数v1或v2越界出错!" << endl;
exit();
} EdgeType *q = new EdgeType(v2, weight);
if(Vertices[v1].adj == NULL)
Vertices[v1].adj = q;
else
{
EdgeType *curr = Vertices[v1].adj, *pre = NULL;
while(curr != NULL && curr->dest < v2)
{
pre = curr;
curr = curr->next;
}
if(pre == NULL)
{
q->next = Vertices[v1].adj;
Vertices[v1].adj = q;
}
else
{
q->next = pre->next;
pre->next = q;
}
}
numOfEdges+=0.5; //边的个数加0.5
}
void AdjTWGraph::DeleteVertex(const int v)
{
EdgeType *pre, *curr;
for(int i = ; i < numVertices; i++)
{
pre = NULL;
curr = Vertices[i].adj;
while(curr != NULL && curr->dest < v)
{
pre = curr;
curr = curr->next;
} if(pre == NULL && curr->dest == v)
{
Vertices[i].adj = curr->next;
delete curr;
numOfEdges--;
}
else if(curr != NULL && curr->dest == v)
{
pre->next = curr->next;
delete curr;
numOfEdges--;
}
} EdgeType *p = Vertices[v].adj, *q;
for(int i = v; i < numVertices-; i++)
Vertices[i] = Vertices[i+];
numVertices--; while(p != NULL)
{
q = p->next;
delete p;
p = q;
numOfEdges--;
}
} void AdjTWGraph::DeleteEdge(const int v1, const int v2)
{
if(v1 < || v1 > numVertices || v2 < || v2 > numVertices)
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
EdgeType *curr = Vertices[v1].adj, *pre = NULL;
while(curr != NULL && curr->dest < v2)
{
pre = curr;
curr = curr->next;
}
if(pre == NULL && curr->dest == v2)
{
Vertices[v1].adj = curr->next;
delete curr;
numOfEdges--;
}
else if(pre != NULL && curr->dest == v2)
{
pre->next = curr->next;
delete curr;
numOfEdges--;
}
else
{
cout << "边<v1, v2>不存在!" << endl;
exit();
}
} int AdjTWGraph::GetFirstNeighbor(const int v)
{
if(v < || v > numVertices)
{
cout << "参数v1越界出错!" << endl;
exit();
}
EdgeType *p = Vertices[v].adj;
if(p != NULL) return p->dest;
else return -;
} int AdjTWGraph::GetNextNeighbor(const int v1, const int v2)
{
if(v1 < || v1 > numVertices || v2 < || v2 > numVertices)
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
EdgeType *p = Vertices[v1].adj;
while(p != NULL)
{
if(p->next != NULL && p->dest == v2) return p->next->dest;
else p = p->next;
}
return -;
} void AdjTWGraph::DepthFirstSearch()
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++) visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(! visited[i])
DepthFirstSearch(i, visited);
delete []visited;
} void AdjTWGraph::DepthFirstSearch(const int v, int visited[])
{
cout<<GetValue(v)<<" ";
visited[v] = ; int w = GetFirstNeighbor(v);
while(w != -)
{
if(! visited[w])
DepthFirstSearch(w, visited);
w = GetNextNeighbor(v, w);
}
} void AdjTWGraph::BroadFirstSearch()
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++) visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(!visited[i]) BroadFirstSearch(i, visited);
delete []visited;
} void AdjTWGraph::BroadFirstSearch(const int v, int visited[])
{
VerT u, w;
SeqQueue queue;
cout<<GetValue(v)<<" ";
visited[v] = ;
queue.Append(v);
while(queue.NotEmpty())
{
u = queue.Delete();
w = GetFirstNeighbor(u);
while(w != -)
{
if(!visited[w])
{
cout<<GetValue(w)<<" ";;
visited[w] = ;
queue.Append(w);
}
w = GetNextNeighbor(u, w);
}
}
}
void AdjTWGraph::Show()
{
for(int i=;i<numVertices;i++)
{
for(int j=;j<numVertices;j++)
{
int a=GetWeight(i,j);
if(a==MaxWeight)
cout<<"∞ ";
else
cout<<a<<" ";
}
cout<<endl;
}
}
CreatAdjTWGraph.h
struct RowColWeight
{
int row; //行下标
int col; //列下标
int weight; //权值
}; void CreatWayWeb(AdjTWGraph &G, DataType V[], int n,RowColWeight E[],int e)
//在图G中插入n个顶点V和e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]); //在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col, E[k].weight);
}
void CreatNoWayWeb(AdjTWGraph &G, DataType V[],int n,RowColWeight E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向网参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight);
G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight);
}
}
SeqQueue.h
#include<iostream>
using namespace std;
class SeqQueue
{
private:
DataType data[MaxQueueSize]; //顺序队列数组
int front; //队头指示器
int rear; //队尾指示器
int count; //元素个数计数器
public:
SeqQueue(void) //构造函数
{front = rear = ; count = ;};
~SeqQueue(void){}; //析构函数 void Append(const DataType& item); //入队列
DataType Delete(void); //出队列
DataType GetFront(void)const; //取队头数据元素
int NotEmpty(void)const //非空否
{return count != ;};
}; void SeqQueue::Append(const DataType& item) //入队列
//把数据元素item插入队列作为当前的新队尾
{
if(count > && front == rear)
{
cout << "队列已满!" << endl;
exit();
} data[rear] = item; //把元素item加在队尾
rear = (rear + ) % MaxQueueSize; ///队尾指示器加1
count++; //计数器加1
} DataType SeqQueue::Delete(void) //出队列
//把队头元素出队列，出队列元素由函数返回
{
if(count == )
{
cout << "队列已空!" << endl;
exit();
} DataType temp = data[front]; //保存原队头元素
front = (front + ) % MaxQueueSize; //队头指示器加1
count--; //计数器减1
return temp; //返回原队头元素
} DataType SeqQueue::GetFront(void)const //取队头数据元素
//取队头元素并由函数返回
{
if(count == )
{
cout << "队列空!" << endl;
exit();
}
return data[front]; //返回队头元素
}
GraphTest.cpp
#include <iostream>
#include <stdlib.h>
const int MaxQueueSize = ; typedef char VerT;
typedef int DistT;
typedef char DataType; #include "AdjTWGraph.h"
#include "CreatAdjTWGraph.h" int main()
{
AdjTWGraph g,f;
char a[] = {'A','B','C','D','E'};
char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{,,},{,,},{,,},{,,},{,,},{,,}};
RowColWeight r2[] ={{,,},{,,},{,,},{,,},{,,},{,,},{,,}};
int n1,n2,e1,e2;
n1=sizeof(a)/sizeof(a[]);
n2=sizeof(b)/sizeof(b[]);
e1=sizeof(r1)/sizeof(r1[]);
e2=sizeof(r2)/sizeof(r2[]);
CreatWayWeb(g, a, n1, r1, e1); //创建有向网
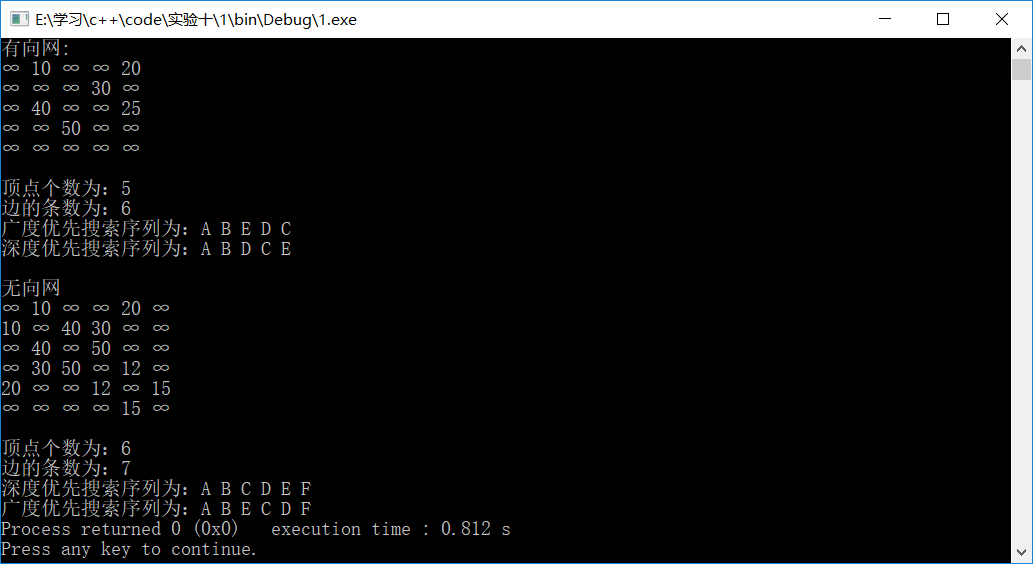
CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl;
g.Show();
cout << "\n顶点个数为：" << g.NumOfVertices();
cout << "\n边的条数为：" << g.NumOfEdges(); cout << "\n广度优先搜索序列为：";
g.BroadFirstSearch();
cout << "\n深度优先搜索序列为：";
g.DepthFirstSearch(); cout<<"\n\n无向网"<<endl;
f.Show();
cout << "\n顶点个数为：" << f.NumOfVertices();
cout << "\n边的条数为：" << f.NumOfEdges();
cout << "\n深度优先搜索序列为：";
f.DepthFirstSearch();
cout << "\n广度优先搜索序列为：";
f.BroadFirstSearch();
return ;
}
最终结果
c++实验10 图的应用实验的更多相关文章
- 实验10.3_数值显示拓展_dword型数转变为表示十进制数的字符串
assume cs:code data segment db 10 dup (0) data ends code segment start : mov ax,4240H;F4240H=1000000 ...
- 20162327WJH实验四——图的实现与应用
20162327WJH实验四--图的实现与应用 实 验 报 告 课程:程序设计与数据结构 班级: 1623 姓名: 王旌含 学号:20162327 成绩: 指导教师:娄嘉鹏 王志强 实验日期:11月2 ...
- c++实验9 图及图的操作实验
实验9 图及图的操作实验 --博客后半部分有程序的所有代码-- 1.图邻接矩阵存储结构表示及基本操作算法实现 (1)邻接矩阵存储结构类定义: #include "SeqList.h" ...
- 20145206《Java程序设计》实验二Java面向对象程序设计实验报告
20145206<Java程序设计>实验二Java面向对象程序设计实验报告 实验内容 初步掌握单元测试和TDD 理解并掌握面向对象三要素:封装.继承.多态 初步掌握UML建模 熟悉S.O. ...
- 20145219 《Java程序设计》实验二 Java面向对象程序设计实验报告
20145219 <Java程序设计>实验二 Java面向对象程序设计实验报告 实验内容 初步掌握单元测试和TDD 理解并掌握面向对象三要素:封装.继承.多态 初步掌握UML建模 熟悉S. ...
- 20145239杜文超 《Java程序设计》实验二 Java面向对象程序设计实验报告
20145239 <Java程序设计>实验二 Java面向对象程序设计实验报告 实验内容 初步掌握单元测试和TDD 理解并掌握面向对象三要素:封装.继承.多态 初步掌握UML建模 熟悉S. ...
- 实验二 PHP基本语法实验
实验二 PHP基本语法实验 0 实验准备 0.1实验环境和相关工具软件 具体到的机房环境,请在Windowsxp环境下做本实验: l 操作系统:Windowsxp l Web服务器:Apache ...
- 20145308刘昊阳 《Java程序设计》实验四 Android环境搭建 实验报告
20145308刘昊阳 <Java程序设计>实验四 Android环境搭建 实验报告 实验名称 Android环境搭建 实验内容 搭建Android环境 运行Android 修改代码,能输 ...
- 20145308刘昊阳 《Java程序设计》实验二 Java面向对象程序设计 实验报告
20145308刘昊阳 <Java程序设计>实验二 Java面向对象程序设计 实验报告 实验名称 Java面向对象程序设计 实验内容 初步掌握单元测试和TDD 理解并掌握面相对象三要素:封 ...
随机推荐
- KVM安装配置笔记
系统环境centos6.6 一.KVM安装前系统相关操作: (1)修改内核模式为兼容内核启动 # grep -v "#" /etc/grub.confdevice (hd0) HD ...
- inetd - 因特网“超级服务”
总览 inetd - [ -d ] [ -q 队列长度 ] [ 配置文件名 ] 描述 inetd通常在系统启动时由/etc/rc.local引导.inetd会监听指定internet端口是否有连接要求 ...
- Inno setup 开源的安装包打包软件
Inno Setup是一个开源的安装包打包软件,下载地址是:http://www.jrsoftware.org/isdl.php 使用引导界面创建一个安装包打包 配置参考官方文档:http://www ...
- 交叉工具链和makefile
交叉工具链: arm-linux-gcc:交叉编译器 arm-linux-ld:交叉连接器 arm-linux-readelf:交叉ELF文件工具 arm-linux-objdump:交叉反汇编器 a ...
- PAT Basic 1047 编程团体赛 (20 分)
编程团体赛的规则为:每个参赛队由若干队员组成:所有队员独立比赛:参赛队的成绩为所有队员的成绩和:成绩最高的队获胜. 现给定所有队员的比赛成绩,请你编写程序找出冠军队. 输入格式: 输入第一行给出一个正 ...
- Java并发编程实战 第13章 显式锁
接口Lock的实现类: ReentrantLock, ReentrantReadWriteLock.ReadLock, ReentrantReadWriteLock.WriteLock Reentra ...
- idea控制台搜索框
https://blog.csdn.net/honnyee/article/details/82772948
- python中一个简单的webserver
python中一个简单的webserver 2013-02-24 15:37:49 分类: Python/Ruby 支持多线程的webserver 1 2 3 4 5 6 7 8 9 10 11 ...
- java面向对象4-多态
5 多态 5.1多态:polymorphism概念 定义:某一类事物的多种存在形态表现形式:父类变量指向子类实例 例:动物中猫,狗 猫这个对象对应的类型是猫类型 猫 x = new 猫(); 同时猫也 ...
- thinkphp读取器和修改器
读取器 如果在模型中,自定义了方法,那么读取器会读取模型中自定义的方法,否则会调用默认的方法. 写入器