[CSP-S模拟测试]:彩球问题（记忆化搜索）

题目传送门（内部题91）

---

输入格式

　　第一行一个正整数$N$，表示颜色种类数。
　　第二行$N$个正整数$k[i],k[i]$表示第$i$种颜色的数量$(1\leqslant k[i]\leqslant 3)$。

---

输出格式

　　一个整数，表示相同颜色的小球不相邻的方案数。

---

样例

样例输入1：

3
1 2 3

样例输出1：

10

样例输入2：

4
1 3 2 1

样例输出2：

96

---

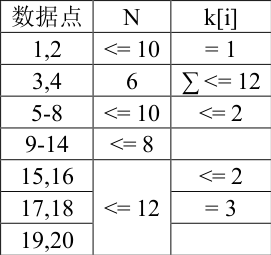
数据范围与提示

输入的所有数字均为正整数。

---

题解

正解（组合数学$+$容斥原理$+$高精度计算$+$动态规划）好麻烦，我不会……

于是就想到了记忆化搜索……

考场上想的是一个$13$维的$DP$……

定义$dp[lst][res1][res2][res3][res4][res5][res6][res7][res8][res9][res10][res11][res12]$分别表示上一位是$lst$，小球$i$还有$res_i$个的方案数……

就为了比别人多骗十分……

再来考虑正解。

设$f[x][i][j][k]$分别上一次放的小球出现的次数为$x$，表示个数为$1$的小球有$i$个，个数为$2$的小球有$j$个，个数为$3$的小球有$k$个。

然后记忆话搜索就好了。

注意可能会爆$long\ long$，但是不会爆$\text{__}int128$。

数据范围中小球的个数可以到$4\sim 5$。

时间复杂度：$\Theta(13^3\times 3)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const long long mod=1e18;
int n;
int k[4];
__int128 dp[3][13][13][13];
__int128 dfs(int lst,int res1,int res2,int res3)
{
	if(dp[lst][res1][res2][res3]!=-1)return dp[lst][res1][res2][res3];
	dp[lst][res1][res2][res3]=0;
	if(lst==0)
	{
		if(res1)dp[lst][res1][res2][res3]+=res1*dfs(0,res1-1,res2,res3);
		if(res2)dp[lst][res1][res2][res3]+=res2*dfs(1,res1+1,res2-1,res3);
		if(res3)dp[lst][res1][res2][res3]+=res3*dfs(2,res1,res2+1,res3-1);
	}
	if(lst==1)
	{
		if(res1>1)dp[lst][res1][res2][res3]+=(res1-1)*dfs(0,res1-1,res2,res3);
		if(res2)dp[lst][res1][res2][res3]+=res2*dfs(1,res1+1,res2-1,res3);
		if(res3)dp[lst][res1][res2][res3]+=res3*dfs(2,res1,res2+1,res3-1);
	}
	if(lst==2)
	{
		if(res1)dp[lst][res1][res2][res3]+=res1*dfs(0,res1-1,res2,res3);
		if(res2>1)dp[lst][res1][res2][res3]+=(res2-1)*dfs(1,res1+1,res2-1,res3);
		if(res3)dp[lst][res1][res2][res3]+=res3*dfs(2,res1,res2+1,res3-1);
	}
	return dp[lst][res1][res2][res3];
}
int main()
{
	memset(dp,-1,sizeof(dp));
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		k[x]++;
	}
	dp[0][0][0][0]=dp[1][0][0][0]=dp[2][0][0][0]=1;
	dfs(0,k[1],k[2],k[3]);
	if(dp[0][k[1]][k[2]][k[3]]>mod)printf("%lld",(long long)(dp[0][k[1]][k[2]][k[3]]/mod));
	printf("%lld",(long long)(dp[0][k[1]][k[2]][k[3]]%mod));
	return 0;
}

---

rp++