【BZOJ3930】[CQOI2015]选数 莫比乌斯反演

【BZOJ3930】[CQOI2015]选数

Description

我们知道，从区间[L,H]（L和H为整数）中选取N个整数，总共有(H-L+1)^N种方案。小z很好奇这样选出的数的最大公约数的规律，他决定对每种方案选出的N个整数都求一次最大公约数，以便进一步研究。然而他很快发现工作量太大了，于是向你寻求帮助。你的任务很简单，小z会告诉你一个整数K，你需要回答他最大公约数刚好为K的选取方案有多少个。由于方案数较大，你只需要输出其除以1000000007的余数即可。

Input

输入一行，包含4个空格分开的正整数，依次为N，K，L和H。

Output

输出一个整数，为所求方案数。

Sample Input

2 2 2 4

Sample Output

3

HINT

样例解释

所有可能的选择方案：(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)

其中最大公约数等于2的只有3组：(2, 2), (2, 4), (4, 2)

对于100%的数据，1≤N,K≤10^9，1≤L≤H≤10^9，H-L≤10^5

题解：先令l=(L-1)/K+1，r=(H-1)/K+1，于是所求变成了：

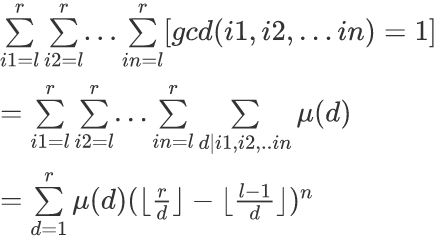
然后用杜教筛，注意l<d的情况

#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#define mod 1000000007
using namespace std;
const int m=1000000;
typedef long long ll;
map<ll,ll> mp;
int num;
int mu[m+10],pri[m/10];
bool np[m+10];
ll sm[m+10];
ll pm(ll x,ll y)
{
	ll z=1;
	while(y)
	{
		if(y&1)	z=z*x%mod;
		x=x*x%mod,y>>=1;
	}
	return z;
}
ll getsm(ll x)
{
	if(x<=m)	return sm[x];
	if(mp.find(x)!=mp.end())	return mp[x];
	ll ret=1,i,last;
	for(i=2;i<=x;i=last+1)
	{
		last=x/(x/i);
		ret=(ret-(last-i+1)*getsm(x/i)+mod)%mod;
	}
	mp[x]=ret;
	return ret;
}
int main()
{
	ll i,j,last,ans=0;
	ll N,K,L,H;
	sm[1]=mu[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,mu[i]=-1;
		sm[i]=sm[i-1]+mu[i];
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
		}
	}
	scanf("%lld%lld%lld%lld",&N,&K,&L,&H),L=(L-1)/K,H=H/K;
	for(i=1;i<=H;i=last+1)
	{
		if(i<=L)	last=min(L/(L/i),H/(H/i));
		else	last=H/(H/i);
		ans=(ans+(getsm(last)-getsm(i-1)+mod)*pm((H/i-L/i),N))%mod;
	}
	printf("%lld",ans);
	return 0;
}