hzau 1202 GCD（矩阵快速幂）

1202: GCD

Time Limit: 1 Sec  Memory Limit: 1280 MB
Submit: 201  Solved: 31
[Submit][Status][Web Board]

Description

 

Input

The first line is an positive integer  T . (1<=T<= 10^3) indicates the number of test cases. In the next T lines, there are three positive integer n, m, p (1<= n,m,p<=10^9) at each line.

Output

Sample Input

1
1 2 3

Sample Output

1

HINT

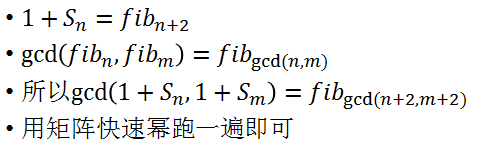
 #include<bits/stdc++.h>
 using namespace std;
 #define ll long long
 #define eps 1e-4
 const int N=1e6+,M=1e6+;

 ///数组大小
 ll MOD;

 struct Matrix
 {
     ll matri[][];
     Matrix()
     {
         memset(matri,,sizeof(matri));
     }
     void init()
     {
         for(int i=;i<;i++)
             for(int j=;j<;j++)
                 matri[i][j]=(i==j);
     }
     Matrix operator + (const Matrix &B)const
     {
         Matrix C;
         for(int i=;i<;i++)
             for(int j=;j<;j++)
                 C.matri[i][j]=(matri[i][j]+B.matri[i][j])%MOD;
         return C;
     }
     Matrix operator * (const Matrix &B)const
     {
         Matrix C;
         for(int i=;i<;i++)
             for(int k=;k<;k++)
                 for(int j=;j<;j++)
                     C.matri[i][j]=(C.matri[i][j]+1LL*matri[i][k]*B.matri[k][j])%MOD;
         return C;
     }
     Matrix operator ^ (const ll &t)const
     {
         Matrix A=(*this),res;
         res.init();
         ll p=t;
         while(p)
         {
             if(p&)res=res*A;
             A=A*A;
             p>>=;
         }
         return res;
     }
 };
 int main()
 {
     Matrix base;  ///初始化矩阵
     base.matri[][]=;base.matri[][]=;
     base.matri[][]=;base.matri[][]=;

     int T;
     scanf("%d",&T);
     while(T--)
     {
         int n,m,p;
         scanf("%d%d%d",&n,&m,&p);
         int x=__gcd(n+,m+);
         MOD=p;
         if(x<=)
             printf("%d\n",%p);
         else
         {
             Matrix ans=base^(x-);
             printf("%lld\n",(ans.matri[][]+ans.matri[][])%MOD);
         }
     }
     return ;
 }