n阶幻方
最近在学习一些经典的算法,搞得头昏脑涨,就想换换脑子。在家里的旧书堆里面乱翻,无意中将一本具有十多年历史的小学数学奥林匹克竞赛的书发掘了出来,能放到现在挺不容易的,就拿起来随便翻翻。看了看目录,一个个熟悉的问题又一次的展现在了我的面前,看着看着就翻到了n阶幻方这块(其实那时候我们不这么叫)。记得当时学这个问题的时候就感觉特别有意思,现在看看也是如此,于是乎便诞生了本片文章。
目录
第一节 n阶幻方问题
第二节 由n阶幻方引发的思考
正文
第一节 n阶幻方问题
所谓n阶幻方问题,俗称“横竖斜相加和相等”(我们当时就是这么叫的)。用术语说就是:在一个N行N列的方格表中,有1,2,3......N*N-1,N*N这N*N个整数,且其对角线、横行、纵行的数字和都相等。
好了,在具体详解该问题之前,我们先看个例子,熟悉一下,如下图所示:

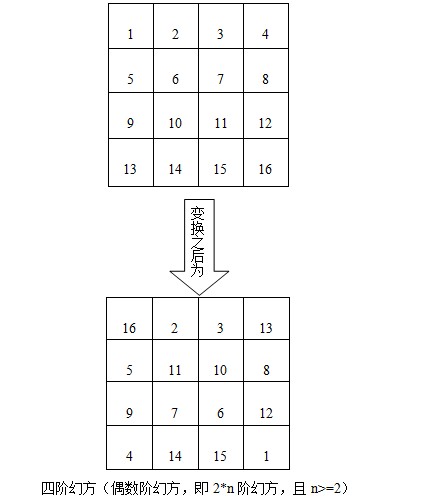
1.奇数阶幻方
我记得基数阶幻方有个口诀,有了这个口诀,走遍奇数幻方都不怕。其实这个口诀也是实现奇数幻方的步骤。
先填上行正中央,
依次斜填切莫忘。
上格没有顶格填,
顶格没有底格放。
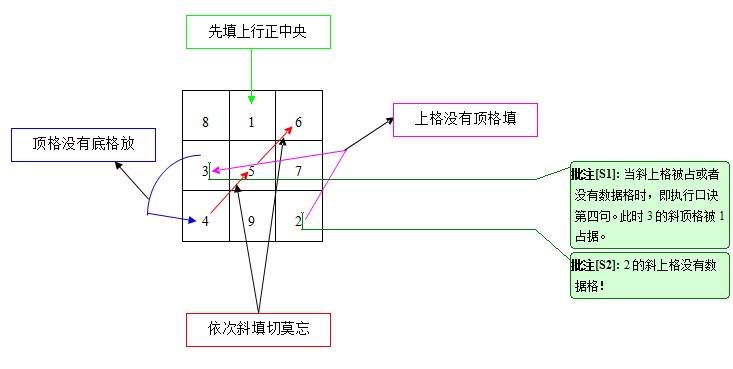
附注:如果上述口诀有什么问题,请留言说明,谢谢!
ok,奇数幻方就讲完了,就这么简单。权当找乐子!
2.偶数阶幻方
说实话,偶数阶幻方我一直以为只有一种,就是2*n阶幻方问题。查了一下才知道偶数阶幻方也分为两小类。
①.4*n阶幻方
4*n阶幻方的生成其实很简单,即对方格中对角线上的数据,先以一条对角线(称对角线一)为对称轴,交换另一对角线(称对角线二)的数据;然后以对角线二为对称轴,交换对角线一的数据。说的直白一点,假设矩阵名为MagicSquare,就是交换MagicSquare[i,j]和MagicSquare[n-1-i,n-1-j]。老办法,作图来说明。图如下:

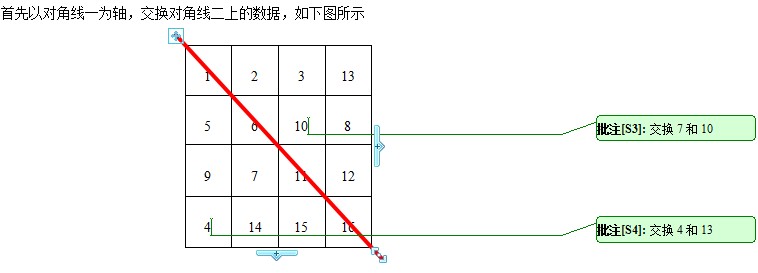

②.4*n+2阶幻方
4*n+2,乍一看就较4*n麻烦了,事实也是如此,不过它的思想也简单。就是将4*n+2看做2*(2*n+1),这样一来就转化成了四个2*n+1求幻方。
附注:下面的我以6阶幻方为例,那么,4*n+2=6,所以n=1。
我通过描述每个步骤加上图形的方式来表述4*n+2阶幻方实现的过程。
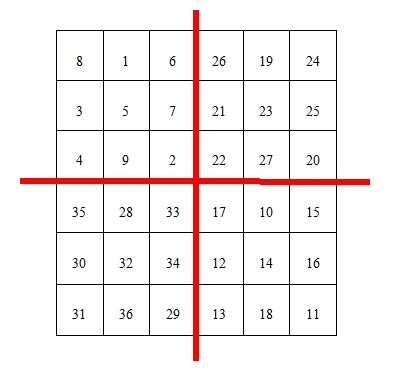
第一步:把整个表格分成4个(2*n+1)*(2*n+1)的小表格,分别叫A,B,C,D。见下图
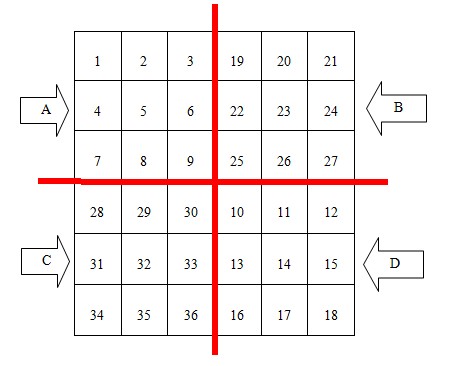
第二步:这样A,B,C,D个小表格就成奇数幻方问题了。
①.将1,2,...,(2*n+1)*(2*n+1)这些数划分给A,并对A实现奇数幻方;
②.将(2*n+1)*(2*n+1)+1,...,2*(2*n+1)*(2*n+1)这些数划分给B,并对B实现奇数幻方;
③.将2*(2*n+1)*(2*n+1)+1,...3*(2*n+1)*(2*n+1)这些数划分C,并对C实现奇数幻方;
④.将3*(2*n+1)*(2*n+1)+1,...4*(2*n+1)*(2*n+1)这些数划分D,并对D实现奇数幻方。
见下图
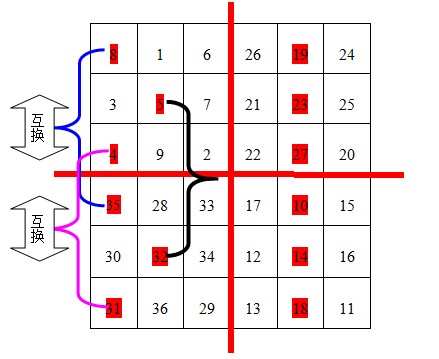
第三步:从A表中的中心(即第n行的MagicSquare[n][n])开始,按照从左向右的方向,标出n个数,A表中的其他行则标出最左边的n格中的数(在图中用红色背景标出)。并且将这些标出的数和C表中的对应位置互换。见下图
第四步:在B表中的中心(如上解释)开始,自右向左,标出n-1列,将B中标出的数据与D表中对应位置的数据交换。但是6阶幻方中,n-1此时等于0,所以B与D不用做交换。
至此,这个幻方就成了,如下图。
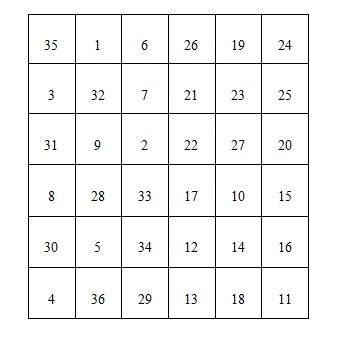
n阶幻方的更多相关文章
- 任意阶幻方(魔方矩阵)C语言实现
魔方又称幻方.纵横图.九宫图,最早记录于我国古代的洛书.据说夏禹治水时,河南洛阳附近的大河里浮出了一只乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服.后人称之为&quo ...
- Java 实现任意N阶幻方的构造
一.关于单偶数阶幻方和双偶数阶幻方 (一)单偶数阶幻方(即当n=4k+2时) 任何4k+2 阶幻方都可由2k+1阶幻方与2×2方块复合而成,6是此类型的最小阶. 以6阶为例,可由3阶幻方与由0,1,2 ...
- Java 实现奇数阶幻方的构造
一.设计的流程图如下所示 二.Java 语言的代码实现 package MagicSquare; //奇数幻方的实现 public class Magic_Odd { //n 为幻方的阶数 publi ...
- hdu1998 bjfu1272奇数阶幻方构造
这题就是一个sb题,本来很水,硬是说得很含混.奇数阶幻方构造其实有好多方法,这题既不special judge,也不说清楚,以为这样能把水题变成难题似的,简直想骂出题人. /* * Author : ...
- Codeforces 710C. Magic Odd Square n阶幻方
C. Magic Odd Square time limit per test:1 second memory limit per test:256 megabytes input:standard ...
- codeforces 710C Magic Odd Square(构造或者n阶幻方)
Find an n × n matrix with different numbers from 1 to n2, so the sum in each row, column and both ma ...
- n阶幻方问题
转载自:http://blog.csdn.net/fengchaokobe/article/details/7437767 目录 第一节 n阶幻方问题 第二节 由n阶幻方引发 ...
- C++求解N阶幻方
由一道数学题的联想然后根据网上的做法瞎jb乱打了一下,居然对了代码精心附上了注释,有兴趣的童鞋可以看一看..不说了,上代码!(自认为结构很清晰易懂) 1234567891011121314151617 ...
- 【C++小白成长撸】--N阶幻方(魔阵)矩阵
解决方法:1.第一个元素放在第一行中间一列 2.下一个元素存放在当前元素的上一行.下一列. 3.如果上一行.下一列已经有内容,则下一个元素的存放位置为当前列的下一行. 在找上一行.下一行或者下一列的时 ...
随机推荐
- Catalan数计算及应用
Catalan数列是非常奇妙的一列数字,因为很多问题的解就是一个Catalan数.知道了这一规律,很多看似复杂的问题便可迎刃而解.那么什么是Catalan数,什么样的问题的解是Catalan数呢? 1 ...
- 使用百度翻译的API接口
http://api.fanyi.baidu.com/api/trans/product/desktop 这是申请的接口地址,会得到一个APPID和一个钥密 然后下载PHP的对应的代码 有一个PHP文 ...
- Linux 搭建NFS文件服务器实现文件共享
我们接着玩Linux,O(∩_∩)O哈哈~ 1.什么是nfs NFS(Network File System)即网络文件系统,是FreeBSD支持的文件系统中的一种,它允许网络中的计算机之间通过TCP ...
- 720. Longest Word in Dictionary 能连续拼接出来的最长单词
[抄题]: Given a list of strings words representing an English Dictionary, find the longest word in wor ...
- Linux中IO监控命令的使用分析
一篇不错的有关linux io监控命令的介绍和使用. 1.系统级IO监控 iostat iostat -xdm 1 # 个人习惯 %util 代表磁盘繁忙程度.100% 表示磁盘 ...
- 模板模式和Comparable类
模板模式中,父类规定好了一些算法的流程,并且空出一些步骤(方法)留给子类填充 Java的数组类中静态方法sort()就是一个模板,它空出了一个compareTo的方法,留给子类填充,用来规定什么是大于 ...
- c语言实践 打印数字三角形
效果如下图: 思路就是外层循环控制要打印的行数,里层循环控制每行打印的数字个数. int val = 65; for (int i = 0; i < 6; i++) { for (int j = ...
- groupie
def add_group(group): c = group.c.astype('float') group['d'] = c/c.sum() return group df = pd ...
- 【linux命令】setterm控制终端属性命令(中英文)
[linux命令]setterm控制终端属性命令(中英文) 2018年03月23日 17:13:44 阅读数:489 标签: linux 更多 个人分类: linux 摘自:https://blog. ...
- POJ2442 Sequence(堆的骚操作)
Description Given m sequences, each contains n non-negative integer. Now we may select one number fr ...
