动态规划---状压dp2

今天模拟，状压dp又没写出来。。。还是不会啊，所以今天搞一下这个状压dp。这里有一道状压dp的板子题：

Corn FieldsCorn Fields

就是一道很简单的状压裸题，但是要每次用一个二进制数表示一行的状态。

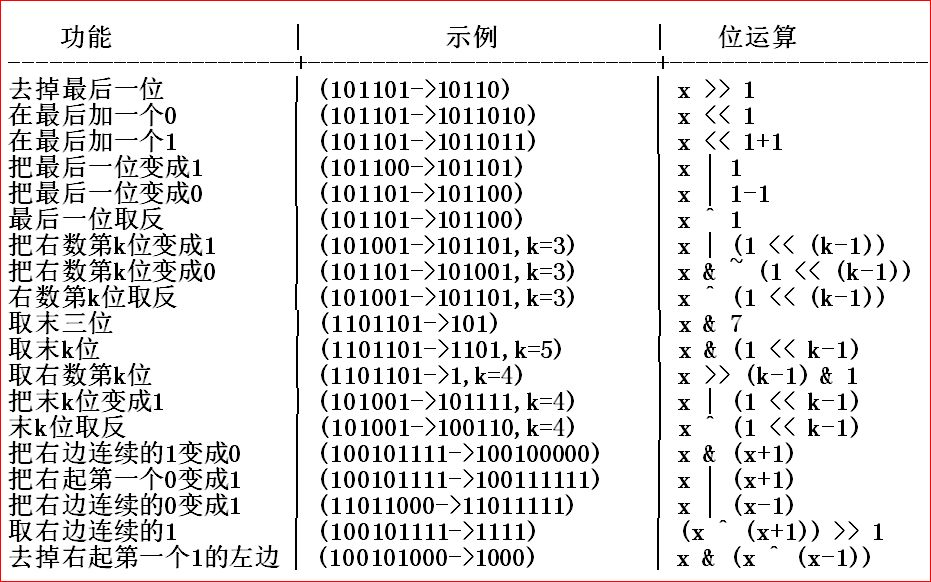
附加一个关于位运算的总结：

上题干：

题目描述

Farmer John has purchased a lush new rectangular pasture composed of M by N ( ≤ M ≤ ;  ≤ N ≤ ) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can't be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.

Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.

农场主John新买了一块长方形的新牧场，这块牧场被划分成M行N列( ≤ M ≤ ;  ≤ N ≤ )，每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。

遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是John不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。

John想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）
输入输出格式
输入格式：

第一行：两个整数M和N，用空格隔开。

第2到第M+1行：每行包含N个用空格隔开的整数，描述了每块土地的状态。第i+1行描述了第i行的土地，所有整数均为0或1，是1的话，表示这块土地足够肥沃，0则表示这块土地不适合种草。

输出格式：

一个整数，即牧场分配总方案数除以100,,000的余数。

输入输出样例
输入样例#： 复制

输出样例#： 复制

题目不用多解释，直接上代码，写注释了，很好懂。

#include<cstdio>
#include<cstring>
using namespace std;
#define duke(i,a,n) for(int i = a;i <= n;i++)
const int mod = 1e9;
template <class T>
void read(T &x)
{
    char c;
    bool op = ;
    while(c = getchar(),c > '' || c < '')
        if(c == '-') op = ;
    x = c - '';
    while(c = getchar(),c <= ''&& c >= '')
        x = x *  + c - '';
    if(op == )
        x = -x;
}
int F[],f[][],m,n,field[][];
int state[];
int main()
{
    read(m);read(n);
    duke(i,,m)
        duke(j,,n)
            read(field[i][j]);
    duke(i,,m)
    {
        duke(j,,n)
        {
            F[i] = (F[i] << ) + field[i][j];//F存i行草地的情况
        }
    }
    f[][] = ;
    int maxn =  << n;
    duke(i,,maxn - )
    {
        state[i] = (((i << ) & i) == ) && (((i >> ) & i) == ); //每种状态是否可行
    }
    duke(i,,m)
        duke(j,,maxn - )
            if(state[j] && ((j & F[i]) == j)) //j是否能选
                duke(k,,maxn - )  //上一排能选什么
                    if((j & k) == )
                        f[i][j] = (f[i][j] + f[i - ][k]) % mod;
    int ans = ;
    duke(i,,maxn - )
    {
        ans += f[m][i];
        ans %= mod;
    }
    printf("%d\n",ans);
    return ;
}