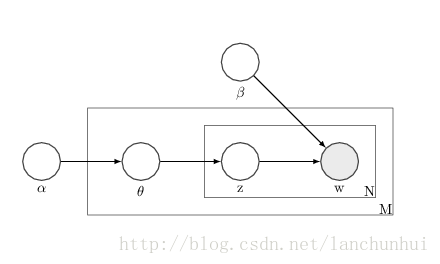
使用 LaTeX 绘制 PGM（Probabilistic Graphical Models）中的贝叶斯网络（bayesian networks）

Software for drawing bayesian networks (graphical models)

这里需要调用 latex 中的绘图库：TikZ and PGF。

注意，下述 tex 代码使用 pdflatex （不是 pdflex）进行编译。

\documentclass[11pt]{report}
\usepackage{tikz}
\usetikzlibrary{fit,positioning}
\begin{document}
\begin{figure}
\centering
\begin{tikzpicture}
\tikzstyle{main}=[circle, minimum size = 10mm, thick, draw =black!80, node distance = 16mm]
\tikzstyle{connect}=[-latex, thick]
\tikzstyle{box}=[rectangle, draw=black!100]

    % 节点的定义，图中的圆
  \node[main, fill = white!100] (alpha) [label=below:$\alpha$] { };
  \node[main] (theta) [right=of alpha,label=below:$\theta$] { };
  \node[main] (z) [right=of theta,label=below:z] {};
  \node[main] (beta) [above=of z,label=below:$\beta$] { };
  \node[main, fill = black!10] (w) [right=of z,label=below:w] { };

    % 边的定义，
  \path (alpha) edge [connect] (theta)
        (theta) edge [connect] (z)
        (z) edge [connect] (w)
        (beta) edge [connect] (w);

    % 节点的定义，图中的矩形
  \node[rectangle, inner sep=0mm, fit= (z) (w),label=below right:N, xshift=13mm] {};
  \node[rectangle, inner sep=4.4mm,draw=black!100, fit= (z) (w)] {};
  \node[rectangle, inner sep=4.6mm, fit= (z) (w),label=below right:M, xshift=12.5mm] {};
  \node[rectangle, inner sep=9mm, draw=black!100, fit = (theta) (z) (w)] {};

\end{tikzpicture}
\end{figure}
\end{document}
%note - compiled with pdflatex