Floyed理解

Floyed理解

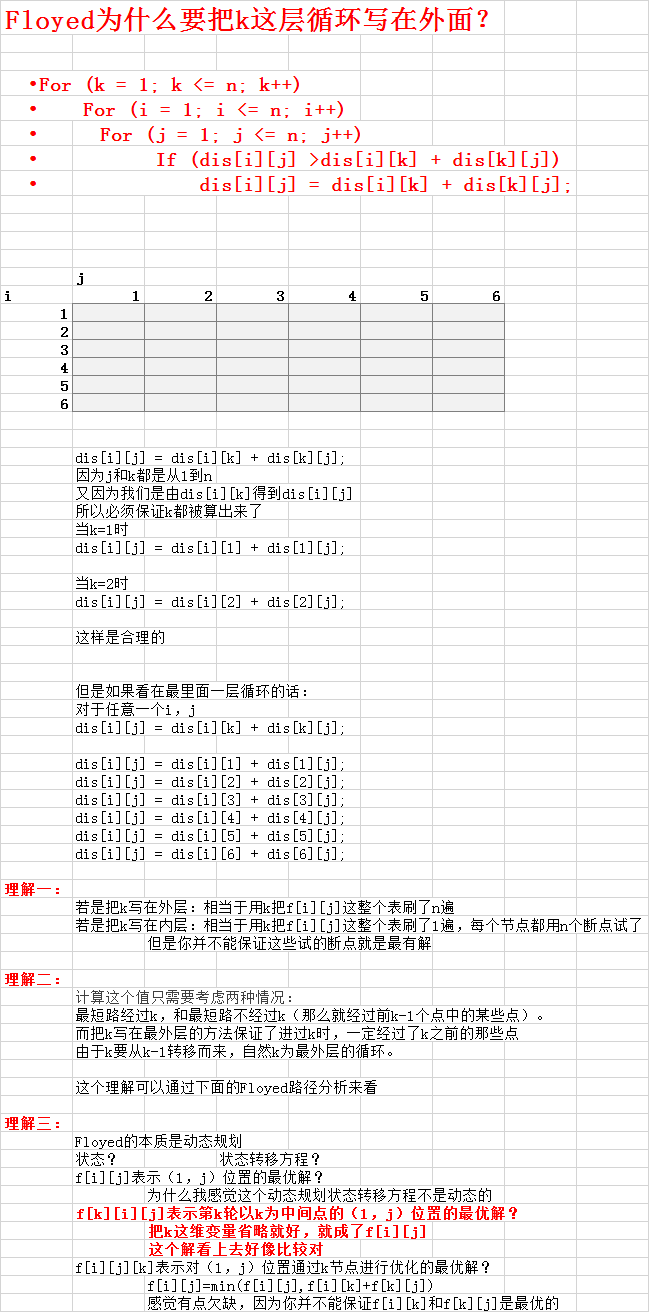
Floyd算法的本质是动态规划，其转移方程为：f(k,i,j) = min( f(k-1,i,j), f(k-1,i,k)+f(k-1,k,j) )。

f(k-1,i,j)表示经过前k-1个点

f(k-1,i,k)+f(k-1,k,j)表示经过k这个点

f(k,i,j)表示路径除开起点i与终点j，只经过前k个点中的某些点，从i到j的最小值。

计算这个值只需要考虑两种情况：最短路经过k，和最短路不经过k（那么就经过前k-1个点中的某些点）。

由于k要从k-1转移而来，自然k为最外层的循环。而经过状态压缩（类似于背包问题）后，就变成了我们熟悉的f(i,j) = min( f(i,j), f(i,k)+f(k,j) )了。

接下来，是Floyd算法的更新过程。归纳一下它的更新过程，其实就是，每一次尝试在每一对节点Vv和Vw之间插入一个节点Vk，如果插入节点后，可以使得Vv和Vw之间的路径变短，那么进行一次更新，否则不更新。

那么，为什么按照这样的规则更新可以找到每对节点间的最短路径呢？我在这里举个例子说明一下，应该就可以把这个问题解释清楚了。假设我们事先已经知道从节点V2到V5之间的最短路径是：V2→V4→V9→V7→V5。

第一步，在初始化过程中，我们获得了(*D)[2][9]、(*D)[9][5]、(*D)[2][5]以及(*P)[2][9]、(*P)[9][5]、(*P)[2][5]的初始值。

第二步，按照Floyd算法进行迭代，迭代到k等于4时，我们会发现在V2和V9之间插入V4之后，V2和V9之间的路径长度达到了史上最低点，(*D)[2][9]更新为(*D)[2][4]+(*D)[4][9]，(*P)[2][9]更新为4。而且在之后的迭代中都不会出现更短的路径，所以(*D)[2][9]和(*P)[2][9]在之后的迭代中都不会发生改变。

第三步，迭代到k等于7时，V9和V5之间的路径长度达到了史上最低点，(*D)[9][5]更新为(*D)[9][7]+(*D)[7][5]，(*P)[9][5]更新为7，此后不再改变。

第四步，迭代到k等于9时，V2和V5之间的路径长度达到了史上最低点，(*D)[2][5]更新为(*D)[2][9]+(*D)[9][5]，(*P)[2][5]更新为9，此后不再改变。这样也就找到了V2和V5之间的最短路径。

现在，我们算出了V2和V5之间的最短路径的长度，但是，怎样找到这条路径的轨迹呢？其实就是根据*P来推断。以上面的例子为例，如果我们要打印V2和V5之间的最短路径的轨迹。首先我们知道(*P)[2][5]=9，初步确定轨迹为V2→V9→V5。根据(*P)[2][9]=4且(*P)[9][5]=7，初步确定轨迹为V2→V4→V9→V7→V5。根据(*P)[2][4]=2，(*P)[4][9]=4，(*P)[9][7]=9，(*P)[7][5]=7，我们可以确定没有新的节点需要加入，所以确定最终的轨迹为V2→V4→V9→V7→V5。

Floyed题目推荐：

【P1119】灾后重建 - 洛谷
https://www.luogu.org/problem/show?pid=1119

【P1078】文化之旅 - 洛谷
https://www.luogu.org/problem/show?pid=1078