【剑指Offer】63、数据流中的中位数

  题目描述：

  如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

  解题思路：

  首先要正确理解此题的含义，数据是从一个数据流中读出来的，因此数据的数目随着时间的变化而增加。对于从数据流中读出来的数据，当然要用一个数据容器来保存，也就是当有新的数据从流中读出时，需要插入数据容器中进行保存。那么我们需要考虑的主要问题就是选用什么样的数据结构来保存。

  方法一：用数组保存数据。数组是最简单的数据容器，如果数组没有排序，在其中找中位数可以使用类比快速排序的partition函数，则插入数据需要的时间复杂度是O(1)，找中位数需要的复杂度是O(n)。除此之外，我们还可以想到用直接插入排序的思想，在每到来一个数据时，将其插入到合适的位置，这样可以使数组有序，这种方法使得插入数据的时间复杂度变为O(n)，因为可能导致n个数移动，而排序的数组找中位数很简单，只需要O(1)的时间复杂度。

  方法二：用链表保存数据。用排序的链表保存从流中的数据，每读出一个数据，需要O(n)的时间找到其插入的位置，然后可以定义两个指针指向中间的结点，可以在O(1)的时间内找到中位数，和排序的数组差不多。

  方法三：用二叉搜索树保存数据。在二叉搜索树种插入一个数据的时间复杂度是O(logn)，为了得到中位数，可以在每个结点增加一个表示子树结点个数的字段，就可以在O(logn)的时间内找到中位数，但是二叉搜索树极度不平衡时，会退化为链表，最差情况仍需要O(n)的复杂度。

  方法四：用AVL树保存数据。由于二叉搜索树的退化，我们很自然可以想到用AVL树来克服这个问题，并做一个修改，使平衡因子为左右子树的结点数之差，则这样可以在O(logn)的时间复杂度插入数据，并在O(1)的时间内找到中位数，但是问题在于AVL树的实现比较复杂。

  方法五：最大堆和最小堆。我们注意到当数据保存到容器中时，可以分为两部分，左边一部分的数据要比右边一部分的数据小。如下图所示，P1是左边最大的数，P2是右边最小的数，即使左右两部分数据不是有序的，我们也有一个结论就是：左边最大的数小于右边最小的数。

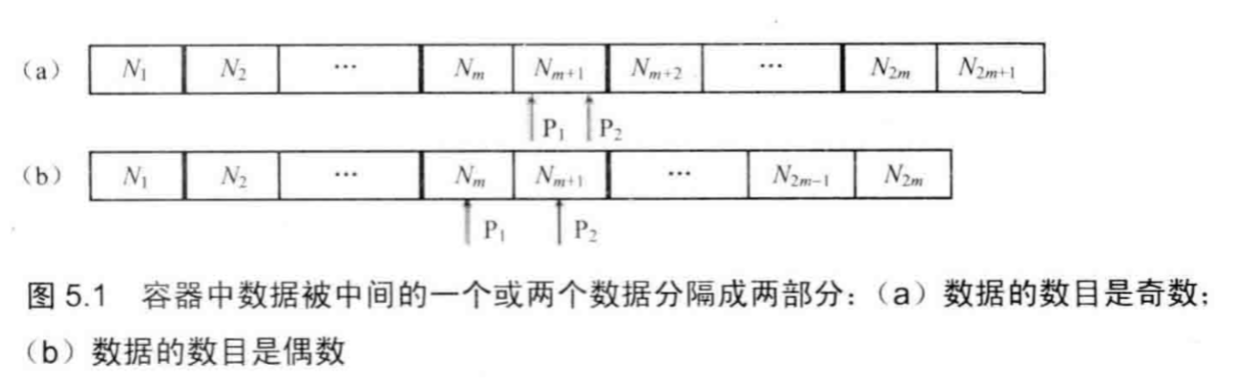
  因此，我们可以有如下的思路：用一个最大堆实现左边的数据存储，用一个最小堆实现右边的数据存储，向堆中插入一个数据的时间是O(logn)，而中位数就是堆顶的数据，只需要O(1)的时间就可得到。

  而在具体实现上，首先要保证数据平均分配到两个堆中，两个堆中的数据数目之差不超过1，为了实现平均分配，可以在数据的总数目是偶数时，将数据插入最小堆，否则插入最大堆。

  此外，还要保证所有最大堆中的数据要小于最小堆中的数据。所以，新传入的数据要和最大堆中最大值或者最小堆中的最小值比较。当总数目是偶数时，我们会插入最小堆，但是在这之前，我们需要判断这个数据和最大堆中的最大值哪个更大，如果最大值中的最大值比较大，那么将这个数据插入最大堆，并把最大堆中的最大值弹出插入最小堆。由于最终插入到最小堆的是原最大堆中最大的，所以保证了最小堆中所有的数据都大于最大堆中的数据。

  总结：

  编程实现（Java）：

import java.util.*;
public class Solution {
    /*
    思路：最大堆和最小堆
    */
    PriorityQueue<Integer> minHeap=new PriorityQueue<>();
    PriorityQueue<Integer> maxHeap=new PriorityQueue<>(new Comparator<Integer>(){
        public int compare(Integer o1,Integer o2){
            return o2-o1;
        }
    });
    int count=0;
    public void Insert(Integer num) {
        count++;
        if(count%2==0){   //偶数，插入最小堆
            if(!maxHeap.isEmpty() && num<maxHeap.peek()){ //如果num小于最大堆，那么先插入最大堆
                maxHeap.add(num);
                num=maxHeap.poll();
            }
            minHeap.add(num);
        }else{ //奇数，插入最大堆
            if(!minHeap.isEmpty() && num>minHeap.peek()){
                minHeap.add(num);
                num=minHeap.poll();
            }
             maxHeap.add(num);
        }
    }

    public Double GetMedian() {
        if(minHeap.size()==maxHeap.size())
            return (minHeap.peek()+maxHeap.peek())/2.0;
        else if(maxHeap.size()>minHeap.size())
            return maxHeap.peek()/1.0;
        else
            return minHeap.peek()/1.0;
    }

}