【转】浅谈对主成分分析(PCA)算法的理解
以前对PCA算法有过一段时间的研究,但没整理成文章,最近项目又打算用到PCA算法,故趁热打铁整理下PCA算法的知识。本文观点旨在抛砖引玉,不是权威,更不能尽信,只是本人的一点体会。
主成分分析(PCA)是多元统计分析中用来分析数据的一种方法,它是用一种较少数量的特征对样本进行描述以达到降低特征空间维数的方法,它的本质实际上是K-L变换。PCA方法最著名的应用应该是在人脸识别中特征提取及数据维,我们知道输入200*200大小的人脸图像,单单提取它的灰度值作为原始特征,则这个原始特征将达到40000维,这给后面分类器的处理将带来极大的难度。著名的人脸识别Eigenface算法就是采用PCA算法,用一个低维子空间描述人脸图像,同时用保存了识别所需要的信息。下面先介绍下PCA算法的本质K-L变换。
1、K-L变换(卡洛南-洛伊(Karhunen-Loeve)变换):最优正交变换
- 一种常用的特征提取方法;
- 最小均方误差意义下的最优正交变换;
- 在消除模式特征之间的相关性、突出差异性方面有最优的效果。
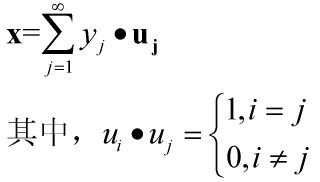


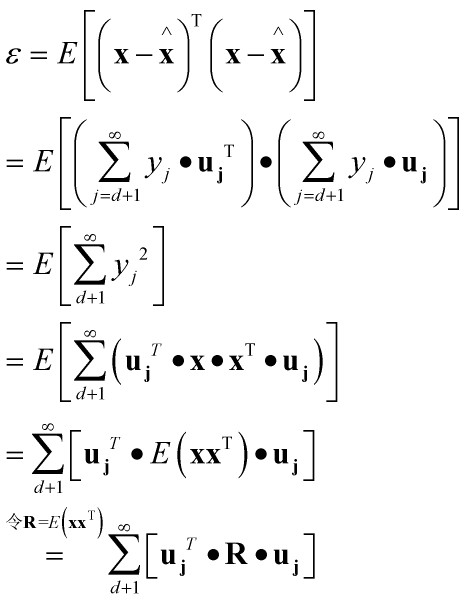


 取得最小值。
取得最小值。
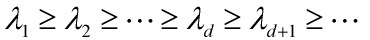



向量y就是变换(降维)后的系数向量,在人脸识别Eigenface算法中就是用系数向量y代替原始特征向量x进行识别。


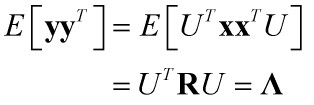
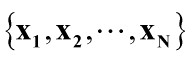 。
。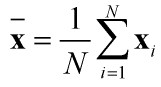
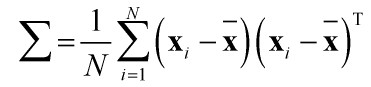
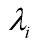 ,这些特征向量组成的矩阵U就是人脸空间的正交基底,用它们的线性组合可以重构出样本中任意的人脸图像,(如果有朋友不太理解这句话的意思,请看下面的总结2。)并且图像信息集中在特征值大的特征向量中,即使丢弃特征值小的向量也不会影响图像质量。
,这些特征向量组成的矩阵U就是人脸空间的正交基底,用它们的线性组合可以重构出样本中任意的人脸图像,(如果有朋友不太理解这句话的意思,请看下面的总结2。)并且图像信息集中在特征值大的特征向量中,即使丢弃特征值小的向量也不会影响图像质量。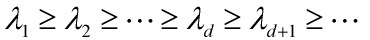 。由大于
。由大于 的
的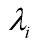 对应的特征向量构成主成分,主成分构成的变换矩阵为:
对应的特征向量构成主成分,主成分构成的变换矩阵为: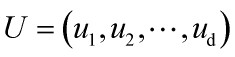
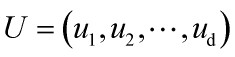 构成的特征脸子空间中,U的维数为M×d。有了这样一个降维的子空间,任何一幅人脸图像都可以向其作投影
构成的特征脸子空间中,U的维数为M×d。有了这样一个降维的子空间,任何一幅人脸图像都可以向其作投影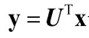 ,即并获得一组坐标系数,即低维向量y,维数d×1,为称为KL分解系数。这组系数表明了图像在子空间的位置,从而可以作为人脸识别的依据。
,即并获得一组坐标系数,即低维向量y,维数d×1,为称为KL分解系数。这组系数表明了图像在子空间的位置,从而可以作为人脸识别的依据。 的特征向量和特征值,这里怎么求的是协方差矩阵
的特征向量和特征值,这里怎么求的是协方差矩阵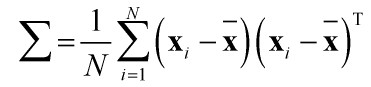 ?
?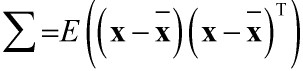 ,可以看出其实
,可以看出其实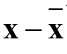 用代替x就成了相关矩阵R,相当于原始样本向量都减去个平均向量,实质上还是一样的,协方差矩阵也是实对称矩阵。
用代替x就成了相关矩阵R,相当于原始样本向量都减去个平均向量,实质上还是一样的,协方差矩阵也是实对称矩阵。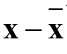 ,则
,则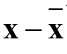 在特征脸空间U的投影,可以表示为系数向量y:
在特征脸空间U的投影,可以表示为系数向量y:
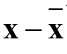 的维数为M×1,y的维数d×1。若M为200*200=40000维,取200个主成分,即200个特征向量,则最后投影的系数向量y维数降维200维。
的维数为M×1,y的维数d×1。若M为200*200=40000维,取200个主成分,即200个特征向量,则最后投影的系数向量y维数降维200维。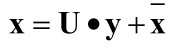
Mat Mat::reshape(int cn, int rows=0) const
该函数是改变Mat的尺寸,即保持尺寸大小=行数*列数*通道数 不变。其中第一个参数为变换后Mat的通道数,如果为0,代表变换前后通道数不变。第二个参数为变换后Mat的行数,如果为0也是代表变换前后通道数不变。但是该函数本身不复制数据。
void Mat::convertTo(OutputArray m, int rtype, double alpha=1, double beta=0 ) const
该函数其实是对原Mat的每一个值做一个线性变换。参数1为目的矩阵,参数2为目d矩阵的类型,参数3和4变换的系数,看完下面的公式就明白了:

PCA::PCA(InputArray data, InputArray mean, int flags, int maxComponents=0)
该构造函数的第一个参数为要进行PCA变换的输入Mat;参数2为该Mat的均值向量;参数3为输入矩阵数据的存储方式,如果其值为CV_PCA_DATA_AS_ROW则说明输入Mat的每一行代表一个样本,同理当其值为CV_PCA_DATA_AS_COL时,代表输入矩阵的每一列为一个样本;最后一个参数为该PCA计算时保留的最大主成分的个数。如果是缺省值,则表示所有的成分都保留。
Mat PCA::project(InputArray vec) const
该函数的作用是将输入数据vec(该数据是用来提取PCA特征的原始数据)投影到PCA主成分空间中去,返回每一个样本主成分特征组成的矩阵。因为经过PCA处理后,原始数据的维数降低了,因此原始数据集中的每一个样本的维数都变了,由改变后的样本集就组成了本函数的返回值。下面由一个图说明:
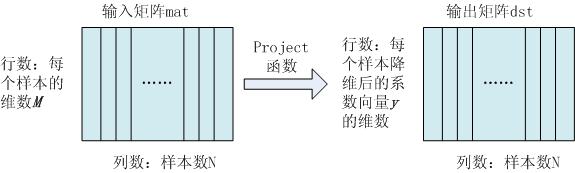
Mat PCA::backProject(InputArray vec) const
一般调用backProject()函数前需调用project()函数,因为backProject()函数的参数vec就是经过PCA投影降维过后的矩阵dst。 因此backProject()函数的作用就是用vec来重构原始数据集(关于该函数的本质就是上面总结2的公式)。由一个图说明如下:
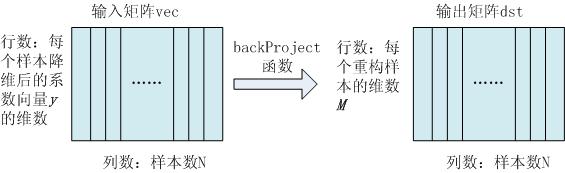
另外PCA类中还有几个成员变量,mean,eigenvectors, eigenvalues等分别对应着原始数据的均值,协方差矩阵的特征值和特征向量。
实验结果:
实验是用4个人人脸图像,其中每个人分别有5张,共计20张人脸图片。用这些图片组成原始数据集来提取他们的PCA主特征脸。该20张图片如下所示:

软件运行结果:
实验中保留4个特征向量作为人脸图像的正交基底,运行结果如下:
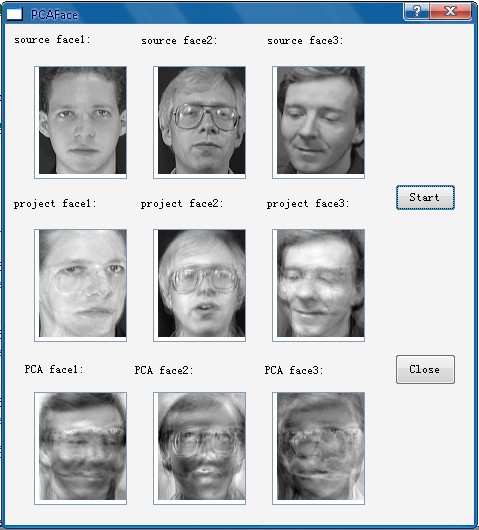
其中第一行的3张人脸分别为20张原图中的3张,这里取的是3个不同人的。
第二行中显示的3张人脸重构的人脸图像,可以看出由于只取了4个特征向量作为正交基底,因此重构后的人脸图像一些细节会丢失。如果增加保留的特征向量个数,则能较好的重构出人脸图像。
第3行的人脸图为取的原始数据协方差矩阵特征向量的最前面3个,因此这3个人脸为最具代表人脸特征的3个PCA人脸特征。
实验主要部分代码:
pcaface.h

1 #ifndef PCAFACE_H
2 #define PCAFACE_H
3 #include <opencv2/core/core.hpp>
4 #include <opencv2/highgui/highgui.hpp>
5 #include <opencv2/imgproc/imgproc.hpp>
6
7 using namespace cv;
8
9 #include <QDialog>
10
11 namespace Ui {
12 class PCAFace;
13 }
14
15 class PCAFace : public QDialog
16 {
17 Q_OBJECT
18
19 public:
20 explicit PCAFace(QWidget *parent = 0);
21 ~PCAFace();
22
23 Mat normalize(const Mat& src);
24
25
26 protected:
27 void changeEvent(QEvent *e);
28
29 private slots:
30 void on_startButton_clicked();
31
32 void on_closeButton_clicked();
33
34 private:
35 Ui::PCAFace *ui;
36 Mat src_face1, src_face2, src_face3;
37 Mat project_face1, project_face2, project_face3;
38 Mat dst;
39 Mat pca_face1, pca_face2, pca_face3;
40 vector<Mat> src;
41 int total;
42 };
43
44 #endif // PCAFACE_H

pcaface.cpp

1 #include "pcaface.h"
2 #include "ui_pcaface.h"
3 #include <QString>
4 #include <iostream>
5 #include <stdio.h>
6
7 using namespace std;
8
9 PCAFace::PCAFace(QWidget *parent) :
10 QDialog(parent),
11 ui(new Ui::PCAFace)
12 {
13 ui->setupUi(this);
14 src_face1 = imread("./images/1.pgm", 0);
15
16 //下面的代码为设置图片显示区域自适应图片的大小
17 ui->face1Browser->setFixedHeight(src_face1.rows+1);
18 ui->face1Browser->setFixedWidth(src_face1.cols+1);
19 ui->face2Browser->setFixedHeight(src_face1.rows+1);
20 ui->face2Browser->setFixedWidth(src_face1.cols+1);
21 ui->face3Browser->setFixedHeight(src_face1.rows+1);
22 ui->face3Browser->setFixedWidth(src_face1.cols+1);
23
24 ui->face4Browser->setFixedHeight(src_face1.rows+1);
25 ui->face4Browser->setFixedWidth(src_face1.cols+1);
26 ui->face5Browser->setFixedHeight(src_face1.rows+1);
27 ui->face5Browser->setFixedWidth(src_face1.cols+1);
28 ui->face6Browser->setFixedHeight(src_face1.rows+1);
29 ui->face6Browser->setFixedWidth(src_face1.cols+1);
30
31 ui->face7Browser->setFixedHeight(src_face1.rows+1);
32 ui->face7Browser->setFixedWidth(src_face1.cols+1);
33 ui->face8Browser->setFixedHeight(src_face1.rows+1);
34 ui->face8Browser->setFixedWidth(src_face1.cols+1);
35 ui->face9Browser->setFixedHeight(src_face1.rows+1);
36 ui->face9Browser->setFixedWidth(src_face1.cols+1);
37
38 for(int i = 1; i <= 15; i++)
39 {
40 stringstream ss;
41 string num;
42 ss<<i; //将整数i读入字符串流
43 ss>>num; //将字符串流中的数据传入num,这2句代码即把数字转换成字符
44 string image_name = ("./images/" + num + ".pgm");//需要读取的图片全名
45 src.push_back(imread(image_name, 0));
46 }
47 total= src[0].rows*src[0].cols;
48 }
49
50 PCAFace::~PCAFace()
51 {
52 delete ui;
53 }
54
55 void PCAFace::changeEvent(QEvent *e)
56 {
57 QDialog::changeEvent(e);
58 switch (e->type()) {
59 case QEvent::LanguageChange:
60 ui->retranslateUi(this);
61 break;
62 default:
63 break;
64 }
65 }
66
67 //将Mat内的内容归一化到0~255,归一化后的类型为但通道整型
68 Mat PCAFace::normalize(const Mat& src) {
69 Mat srcnorm;
70 cv::normalize(src, srcnorm, 0, 255, NORM_MINMAX, CV_8UC1);
71 return srcnorm;
72 }
73
74
75 void PCAFace::on_startButton_clicked()
76 {
77 //先显示3张原图
78 ui->face1Browser->append("<img src=./images/1.pgm>");
79 ui->face2Browser->append("<img src=./images/7.pgm>");
80 ui->face3Browser->append("<img src=./images/14.pgm>");
81
82 //mat数组用来存放读取进来的所有图片的数据,其中mat的每一列对应1张图片,该实现在下面的for函数中
83 Mat mat(total, src.size(), CV_32FC1);
84 for(int i = 0; i < src.size(); i++)
85 {
86 Mat col_tmp = mat.col(i);
87 src[i].reshape(1, total).col(0).convertTo(col_tmp, CV_32FC1, 1/255.);
88 }
89 int number_principal_compent = 4; //保留最大的主成分数
90
91 //构造pca数据结构
92 PCA pca(mat, Mat(), CV_PCA_DATA_AS_COL, number_principal_compent);
93
94
95 //pca.eigenvectors中的每一行代表输入数据协方差矩阵一个特征向量,且是按照该协方差矩阵的特征值进行排序的
96 pca_face1 = normalize(pca.eigenvectors.row(0)).reshape(1, src[0].rows); //第一个主成分脸
97 imwrite("./result/pca_face1.jpg", pca_face1);//显示主成分特征脸1
98 ui->face7Browser->append("<img src=./result/pca_face1.jpg>");
99
100 pca_face2 = normalize(pca.eigenvectors.row(1)).reshape(1, src[0].rows); //第二个主成分脸
101 imwrite("./result/pca_face2.jpg", pca_face2);//显示主成分特征脸2
102 ui->face8Browser->append("<img src=./result/pca_face2.jpg>");
103
104 pca_face3 = normalize(pca.eigenvectors.row(2)).reshape(1, src[0].rows); //第三个主成分脸
105 imwrite("./result/pca_face3.jpg", pca_face3);//显示主成分特征脸3
106 ui->face9Browser->append("<img src=./result/pca_face3.jpg>");
107
108 //将原始数据通过PCA方向投影,即通过特征向量的前面几个作用后的数据,因此这里的dst的尺寸变小了
109 dst = pca.project(mat);
110
111 //通过方向投影重构原始人脸图像
112 project_face1 = normalize(pca.backProject(dst).col(1)).reshape(1, src[0].rows);
113 imwrite("./result/project_face1.jpg", project_face1);
114 ui->face4Browser->append("<img src=./result/project_face1.jpg>");
115
116 project_face2 = normalize(pca.backProject(dst).col(7)).reshape(1, src[0].rows);
117 imwrite("./result/project_face2.jpg", project_face2);
118 ui->face5Browser->append("<img src=./result/project_face2.jpg>");
119
120 project_face3 = normalize(pca.backProject(dst).col(14)).reshape(1, src[0].rows);
121 imwrite("./result/project_face3.jpg", project_face3);
122 ui->face6Browser->append("<img src=./result/project_face3.jpg>");
123 }
124
125 void PCAFace::on_closeButton_clicked()
126 {
127 close();
128 }

实验的工程代码可以在上面的那个链接下载,环境搭建可以参考我之前写个一个文章http://www.cnblogs.com/liu-jun/archive/2012/09/26/Jacky_Liu.html。
作者:Jacky_Liu,转载或分享请注明出处。
【转】浅谈对主成分分析(PCA)算法的理解的更多相关文章
- [原创]浅谈在创业公司对PMF的理解
[原创]浅谈在创业公司对PMF的理解 在创业时,大多数人都常谈一个词叫"MVP“,但PMF谈的比较少,PMF在创业公司尤为重要,以下谈谈个人一些看法. 1.什么是PMF? 创业公司:一种是找 ...
- [原创]浅谈在创业公司对MVP的理解
[原创]浅谈在创业公司对MVP的理解 目前自已所处的公司类似一个创业平台,我们内部会不断的去孵化不同方向的产品,产品经理经常谈到的一个词就是MVP,所以有必需要去了解下什么是MVP? 1 什么是MVP ...
- [随机化算法] 听天由命?浅谈Simulate Anneal模拟退火算法
Simulate Anneal模拟退火算法,是一种用于得到最优解的随机化算法. 如果可以打一手漂亮的随机化搜索,也许当你面对一筹莫展的神仙题时就有一把趁手的兵器了. 这篇题解将教你什么?SA的基本思路 ...
- 机器学习--主成分分析(PCA)算法的原理及优缺点
一.PCA算法的原理 PCA(principle component analysis),即主成分分析法,是一个非监督的机器学习算法,是一种用于探索高维数据结构的技术,主要用于对数据的降维,通过降维可 ...
- 主成分分析 PCA算法原理
对同一个体进行多项观察时,必定涉及多个随机变量X1,X2,…,Xp,它们都是的相关性, 一时难以综合.这时就需要借助主成分分析 (principal component analysis)来概括诸多信 ...
- Python的主成分分析PCA算法
这篇文章很不错:https://blog.csdn.net/u013082989/article/details/53792010 为什么数据处理之前要进行归一化???(这个一直不明白) 这个也很不错 ...
- 大数质因解:浅谈Miller-Rabin和Pollard-Rho算法
2017-07-19 08:54 Amphetamine:能发一下代码吗? 应我那位谜一样好友的邀约,我打算好好看一看Miller-Rabin和Pollard-Rho算法.很奇怪,各种地方有很多代码描 ...
- 浅谈Java数据结构和算法
今天的突然看集合底层的时候发现了好多算法和数据结构.再次就比较一下和汇总一下. 数据结构分类:线性结构和非线性结构 问题一: 什么是线性和非线性: 我个人的理解是:数据结构中线性结构指的是数据元素之间 ...
- 浅谈对ST表的一些理解
今天打了人生第一道ST表题(其实只是ST表跑得最快); ST表是一种用来解决RMQ问题的利器... 大体操作有两步: 第一部分nlogn预处理 第二部分O(1)询问 预处理就是运用倍增+区间动规 ST ...
随机推荐
- 前端面试题整理---JS基础
为了督促自己学习,整理了一下前端的面试题 JavaScript: JavaScript 中如何监测一个变量是String类型? typeof(obj)==="string"; ty ...
- c# json字符串转数组
JArray jo = (JArray)JsonConvert.DeserializeObject("这里是json字符串");
- Ubuntu14.04 使用scp远程传输命令进行服务器文件互传
1.将另一个服务器上的文件拷贝到本地 sudo scp host_name@host_ip:/home/aaa/bbb /ccc/ddd/bbb 上面命令的意思是将远程服务器/home/aaa/目录下 ...
- Java VisualVM添加Visual GC插件
1.访问地址:https://visualvm.github.io/pluginscenters.html,找到自己JDK版本对应的插件下载地址(我的JDK版本为1.7.0_67): 2.点击该链接进 ...
- SQL server 游标,随机数使用
SELECT * FROM [goods] DECLARE test_cursor CURSOR scroll FOR SELECT goods_no, [unitprice] FROM [goods ...
- 语义分割丨PSPNet源码解析「测试阶段」
引言 本文接着上一篇语义分割丨PSPNet源码解析「网络训练」,继续介绍语义分割的测试阶段. 模型训练完成后,以什么样的策略来进行测试也非常重要. 一般来说模型测试分为单尺度single scale和 ...
- 重置 linux系统后要配置的基本组件操作
1.安装jdk https://www.cnblogs.com/shihaiming/p/5809553.html 2.安装mysql 3.安装tomcat
- vuex填坑记录
vuex是需要等待页面加载完成后才会更新的,如果页面点击刷新有用到vuex的地方,那么vuex会保持旧的数据,等刷新完成后vuex的数据才会重置,所以要在页面加载后再调用vuex的数据才是正确的,如果 ...
- java实现xml文件读取并保存到对象
首先浅聊一下解析xml的四种方式: 1.DOM方式:有缺点但是这个缺点却也是他的优点.下面详细介绍: 以树形的层次结构组织节点或信息片断集合,可以获得同一个文档中的多处不同数据.使用起来简单. 优点是 ...
- SQL查询-约束-多表
一.SQL语句查询 1.聚合函数 COUNT()函数,统计表中记录的总数量 注:COUNT()返回的值为Long类型;可通过Long类的intValue()方法 ...
