UVALive - 8292 （法里数列）

参考博客：zro https://blog.csdn.net/alusang/article/details/81840944 orz

给你一个分母 m 和一个浮点数 x，让你求出一个分母不超过 m 的分数值最接近 x 的分数。

最终答案要求是最简分数。

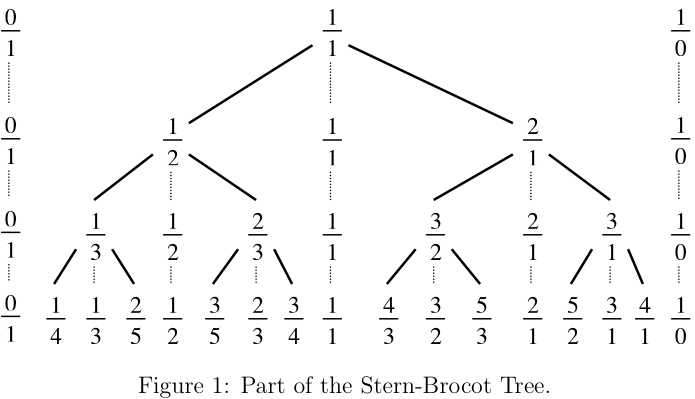
数学上，n阶的法里数列是0和1之间最简分数的数列，由小至大排列，每个分数的分母不大于n。

法里数列的排列如上图。两个法里数中间的数字 = 分子的和 / 分母的和

所以可以二分找最接近给出的浮点数的法里数。

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iostream>
using namespace std;
int main()
{
    int t;
    scanf("%d", &t);
    for (int ca = ; ca <= t; ca++)
    {
        int id, m;
        double x;
        scanf("%d%d%lf", &id, &m, &x);

        int a, b, c, d;
        a = , b = c = d = ;
        while()
        {
            int fz = a+c, fm = b+d;
            int g = __gcd(fz, fm);

            fz /= g, fm /= g;
            if (fm > m) break;

            if (1.0*fz/fm < x) a = fz, b = fm;
                else c = fz, d = fm;
        }

        printf("%d ", id);
        if (fabs(1.0*a/b-x) > fabs(1.0*c/d-x)) printf("%d/%d\n", c, d);
            else printf("%d/%d\n", a, b);
    }
}