理解机器为什么可以学习（三）---Theory of Generalization

前边讨论了我们介绍了成长函数和break point，现在继续讨论m是否成长很慢，是否能够取代M。

成长函数就是二分类的排列组合的数量。break point是第一个不能shatter（覆盖所有情形）的点。

1.break point对成长函数的限制

我们希望

这里引入上限函数 bound function:给了break point，看看可以组成多少排列组合，下面证明boundfunction是多项式成长的。

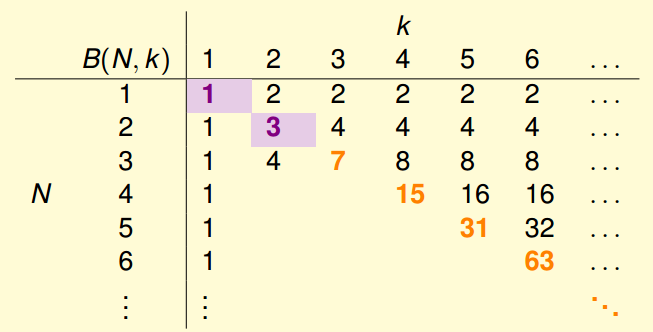
右上角相当于没有加条件限制，对角线就是全部的减1嘛，因为全部不可能，小一点，找个上限。

接下来填剩余部分，通过转换得到B(4, 3) = B(3, 3) + B(3,2)

所以得到，

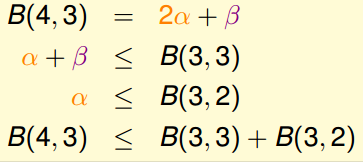
同理得到，

由数学归纳法可以证明：

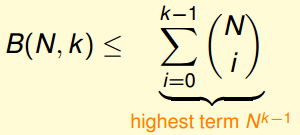
所以，我们就得到：成长函数会被上限函数bound住，上限函数会被上限函数的上限函数bound住，上限函数的上限会被一个与break point有关的多项式bound住。

接下来，我们回到最之前的Hoeffding不等式转换式：

接下来证明它们。

由于Eout是无限个点的，因此我们不能直接带入上限，现在想办法转化，类似于交叉验证，现在选择一个Ein'，那么有，

所以，最终我们得到，

对于PLA来说，由于我们知道4是一个break point，所以最终成长函数会被限制住，也就是learning是可以的。

下一节引入VC Bound继续解释为什么机器可以学习。http://www.cnblogs.com/futurehau/p/6260332.html