【BZOJ 2243】染色

传送门：洛谷   BZOJ

还不会LCT的小伙伴可以看一下这篇博客：LCT总结

我初学动态树时就是看着那篇博客学的，写的很好！

那好 言归正传。

显然树上 x 到 y 的路径的问题都可以用LCT Access一下把路径剖离出来，那主要问题在于如何用Splay 来维护颜色呢？

上图(XP 灵魂画手）

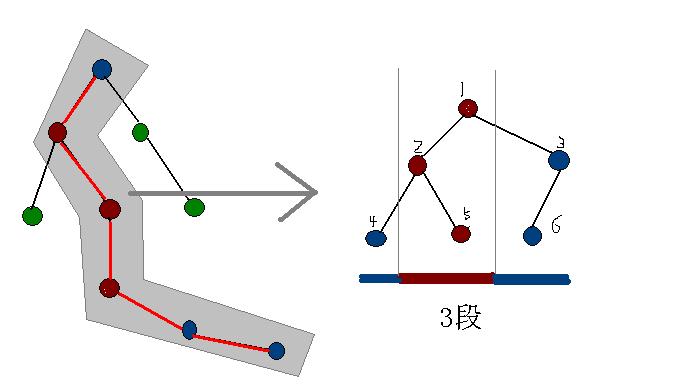
对于Splay树的每一个节点，维护四个信息

c[x] : 节点本身的颜色

cL[x]: 节点对应子树最左端的颜色

cR[x]: 节点对应子树最右端的颜色

tot[x]: 节点对应子树区间的颜色段数

所以upDATA的时候就很显然啦~

 void pUP(int x){
     int lc=ch[x][],rc=ch[x][];

     cL[x]= lc? cL[lc]:c[x];
     cR[x]= rc? cR[rc]:c[x];

     if(lc && rc) tot[x]=tot[lc]+tot[rc]+-(cR[lc]==c[x])-(cL[rc]==c[x]);

     if(lc &&!rc) tot[x]=tot[lc]+-(cR[lc]==c[x]);

     if(!lc&& rc) tot[x]=tot[rc]+-(cL[rc]==c[x]);

     if(!lc&&!rc) tot[x]=;
 }

其他部分就和平常的LCT没有什么区别了

哦 对，pushDOWN时要注意 区间翻转，cL和cR要一起翻

全代码~

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<algorithm>

 #define For(i,a,b) for(register int i=a;i<=b;++i)
 #define Dwn(i,a,b) for(register int i=a;i>=b;--i)
 #define Pn putchar('\n')
 #define I inline
 #define Re register

 using namespace std;

 const int N=1e5+;

 int ch[N][],fa[N],c[N],cL[N],cR[N],tot[N],tag[N],st[N],top,tgC[N];
 int n,m,x,y,z;
 char opt;

 I void read(int &v){
     v=;
     char c=getchar();
     while(c<''||c>'')c=getchar();
     while(c>=''&&c<='')v=v*+c-'',c=getchar();
 }
 void write(int x){
     if(x>)write(x/);
     int xx=x%;
     putchar(xx+'');
 }
 I bool NOrt(int x){
     return ch[fa[x]][]==x || ch[fa[x]][]==x;
 }
 I void pTAG(int x){
     swap(ch[x][],ch[x][]);
     swap(cL[x],cR[x]);
     tag[x]^=;
 }
 I void pTGC(int x,int Col){
     c[x]=cL[x]=cR[x]=Col;
     tot[x]=;
     tgC[x]=Col;
 }
 I void pDOWN(int x){
     if(tag[x]){
         if(ch[x][])pTAG(ch[x][]);
         if(ch[x][])pTAG(ch[x][]);
         tag[x]^=;
     }
     if(tgC[x]){
         if(ch[x][])pTGC(ch[x][],tgC[x]);
         if(ch[x][])pTGC(ch[x][],tgC[x]);
         tgC[x]=;
     }
 }
 I void pUP(int x){
     int lc=ch[x][],rc=ch[x][];

     cL[x]= lc? cL[lc]:c[x];
     cR[x]= rc? cR[rc]:c[x];

     if(lc && rc) tot[x]=tot[lc]+tot[rc]+-(cR[lc]==c[x])-(cL[rc]==c[x]);

     if(lc &&!rc) tot[x]=tot[lc]+-(cR[lc]==c[x]);

     if(!lc&& rc) tot[x]=tot[rc]+-(cL[rc]==c[x]);

     if(!lc&&!rc) tot[x]=;
 }
 I bool Wson(int x){
     return ch[fa[x]][]==x;
 }
 I void Rotate(int x){
     int y=fa[x];
     int z=fa[y];
     int ws=Wson(x);
     if(NOrt(y))ch[z][Wson(y)]=x;
     fa[x]=z;

     ch[y][ws]=ch[x][ws^];
     if(ch[x][ws^])fa[ch[x][ws^]]=y;

     ch[x][ws^]=y;
     fa[y]=x;

     pUP(y); pUP(x);
 }
 I void Splay(int x){
     top=; int now=x;
     st[++top]=now;
     while(NOrt(now))st[++top]=now=fa[now];
     while(top) pDOWN(st[top--]);

     while(NOrt(x)){
         int y=fa[x];
         if(NOrt(y)){
             if(Wson(y)==Wson(x))Rotate(y);
             else Rotate(x);
         }
         Rotate(x);
     }
 }
 I void Access(int x){
     int lst=;
     while(x){
         Splay(x); ch[x][]=lst; pUP(x);
         lst=x; x=fa[x];
     }
 }
 I void ChangeRt(int x){
     Access(x); Splay(x); pTAG(x);
 }
 I void Link(int x,int y){
     ChangeRt(x); fa[x]=y;
 }
 I void Split(int x,int y){
     ChangeRt(x); Access(y); Splay(y);
 }
 int main(){
     read(n); read(m);
     For(i,,n){
         read(c[i]); tot[i]=;
         cL[i]=cR[i]=c[i];
     };
     For(i,,n-){
         read(x); read(y);
         Link(x,y);
     }
     For(i,,m){
         opt=getchar();
         while(opt!='C'&&opt!='Q')opt=getchar();
         if(opt=='C'){
             read(x); read(y); read(z);
             Split(x,y); pTGC(y,z);
         }
         if(opt=='Q'){
             read(x); read(y);
             Split(x,y);
             write(tot[y]); Pn;
         }
     }
     return ;
 }